Maceió — Winter 2019
July 2020
Notes for a course in cryptologoy that introduces
Python), andcryptography.
In this course, you will learn about
The recommended reading will introduce you to the most important authors and articles in cryptology.
On completion of this chapter, you will have learned …
Cryptography serves to protect information by encryption (or enciphering), the shuffling of data (that is, the transformation of intelligible into indecipherable data) that only additional secret information, the key, can feasibly undo it (decryption or deciphering).
encrypt/encipher: to shuffle data so that only additional secret information can feasibly undo it.
key: the additional secret information that is practically indispensable to decrypt.
decrypt/decipher: to invert encryption.
That is, the shuffled (enciphered) data can practically only be recovered (deciphered) by knowledge of the key. Since the original data is in principle still recoverable, it can be thought of as concealment.
Because historically only written messages were encrypted, the source
data, though a string of 1s and 0s (the
viewpoint adopted in symmetric cryptography) or a number (that adopted
in asymmetric cryptography), is called plaintext and the
encrypted data the ciphertext.
plaintext respectively ciphertext: the data to be encrypted respectively the encrypted data.
Historically, the key to reverse this transformation (of intelligible data into indecipherable data) was both necessary to decipher and to encipher, symmetric encryption. That is, in the past, the key used to encrypt and decrypt was always the same: Symmetric cryptography had been used by the Egyptians almost 2000 years before Christ, and was used, for example,
Engima machine, andAES algorithm).symmetric cryptography: cryptography is symmetric when the same key is used to encrypt and decrypt.
In the 70s asymmetric cryptography was invented, in which the key to encipher (the public key) and the key to decipher (the secret or private key) are different.
asymmetric cryptography: cryptography is asymmetric when different keys are used to encrypt and decrypt. The key to encipher is public and the key to decipher is private (or secret).
In fact, only the key to decipher is private, kept secret, while the key to encrypt is public, known to everyone. In comparison with symmetric cryptography, asymmetric encryption avoids the risk of compromising the key to decipher that is involved
On top, It is useful, that the keys exchange their roles, the private key enciphers, and the public one deciphers, a digital signature: While the encrypted message will no longer be secret, every owner of the public key can check whether the original message was encrypted by the private key.
Nowadays such asymmetric cryptography algorithms are ubiquitous on the Internet: Examples are
RSA which is based on the difficulty of factoring in
prime numbers, orECC which is based on the difficulty of computing
points in finite curves,which protect (financial) transactions on secure sites (those indicated by a padlock in the browser’s address bar).
Up to the digital age, cryptography mainly studied the transformation of intelligle text into indecipherable text. Since then, cryptography studies the transformation of processible (digital) data into indecipherable (digital) data. This data is, for example, a digital file (text, image, sound, video, …). It is considered a bit sequence (denoted by a string of 0s and 1s) or byte sequence (denoted by a string of hexadecimal pairs 00, 01, …, FE, FF) or a number (denoted as usual by their decimal expansion 0, 1, 2, 3 …). Let us recall that every bit sequence is a number via its binary expansion (and vice versa).
The point of view of a sequence of bits (or, more exactly, of
hexadecimal digits whose sixteen symbols 0 – 9
and A – F correspond to a group of four bits)
is preferred in symmetric cryptography whose algorithms transform them,
for instance, by permutation and substitution of their digits. The point
of view of a number is preferred in asymmetric cryptography whose
algorithms operate on it by mathematical functions such as raising to a
power (raising to a power) and exponentiation.
The key, the additional secret information, can take various form; which form is mainly a question of convenience, most common are:
For example, in the ancient Scytale algorithm (see
Section 2) that uses a role of parchment
wrapped around a stick, the key consists of the circumference (in
letters) of the stick, a small number. Nowadays, PIN codes
(= Personal Identification Number) or passwords are ubiquitous in
day-to-day life; to facilitate memorization the memorization of complete
secret sentences (= pass phrases) is encouraged.
Asymmetric encryption depends on larger keys and therefore stores
them in files (of 64-letter texts, called ASCII-armor) of a
couple of kilobytes. For example (where ... indicates tens
of skipped lines):
-----BEGIN PGP PUBLIC KEY BLOCK-----
Version: SKS 1.1.6
Comment: Hostname: pgp.mit.edu
mQENBFcFAs8BCACrW3TP/ZiMRQJqWP0SEzXqm2cBZ+fyBUrvcu1fGU890pd4
3JdiWIreHx/sbJdW1wjABeW8xS1bM67nLW9VVHUPLi9QP3VGfmqmXqbWIB7O
...
-----END PGP PUBLIC KEY BLOCK-----The prefix Crypto-, comes from Greek kryptós, “hidden”.
Cryptography (from the Greek gráphein, “to write”) is the art of hidden writing: shuffling information so that it is indecipherable to all but the intended recipient.
Cryptography: the art of transforming information so that it is indecipherable to all but the intended recipient.
That is, cryptography is the art of transforming information such that it is incomprehensible to all but the intended recipient. Useful, since Antiquity, for example to conceal military messages from the enemy. Since then, (electronic binary) data has replaced text, and what used to be concealing written messages exchanged by messengers or kept secret has become symmetric cryptography: securing data flowing between computers or stored on a computer.
Since the 70s, asymmetric cryptography makes it possible (by digital signatures) to verify the identities of participants and undeniably (non-repudiation) register their transactions in electronic commerce.
Cryptographic methods (or Ciphers) are generically classified
AES, or different keys to encrypt and decrypt
(asymmetric, or two-key, or public-key)
cipher, such as RSA or ECC.Among the symmetric ciphers, these are generically classified
AES or
RSA) or single bits (stream ciphers such as
RC4): While stream ciphers typically are simpler, faster
and predestined for real time transmissions, they tend to be less secure
and are therefore less commonly used (for example, a Wi-Fi network is
commonly secured by a block cipher such as AES).Cryptanalysis (from the Greek analýein, “to unravel”) is the art of untying the hidden writing: the breaking of ciphers, that is, recovering or forging enciphered information without knowledge of the key.
Cryptanalysis: the art of deciphering ciphertext without knowledge of the key.
Cryptanalysis (colloquially “code breaking”) is the art of deciphering the enciphered information without knowledge of the secret information, the key, that is normally required to do so; usually by finding a secret key.
Cryptanalysis of public-key algorithms relies on the efficient
computation of mathematical functions on the integers. For instance,
cryptanalysis of the most famous public-key algorithm, RSA
, requires the factorization of a number with
decimal digits into its prime factors, which is computationally
infeasible (without knowledge of the key).
Cryptanalysis of symmetric ciphers depends on the propagation of
patterns in the plaintext to the ciphertext. For example, in a
monoalphabetic substitution cipher (in which each letter is
replaced by another letter, say A by Z), the
numbers of occurrences with which letters occur in the plaintext
alphabet and in the ciphertext alphabet are identical (if A
occurred ten times, then so does Z). If the most frequent
letters of the plaintext can be guessed, so those of the ciphertext.
A powerful technique is Differential cryptanalysis that studies how differences (between two plaintexts) in the input affect those at the output (of the corresponding ciphertexts). In the case of a block cipher, it refers to tracing the (probabilities of) differences through the network of transformations. Differential cryptanalysis attacks are usually Chosen-plaintext attacks, that is, the attacker can obtain the corresponding ciphertexts for some set of plaintexts of her choosing.
Cryptology (from the Greek lógos, “word”, “reason”, “teaching” or “meaning”) is the science of hiding, the science of trusted communication which embraces cryptography and cryptanalysis; according to Webster (1913) it is “the scientific study of cryptography and cryptanalysis”. Though cryptology is often considered a synonym for cryptography and occasionally for cryptanalysis, cryptology is the most general term.
Cryptology: the science of trusted communication, including cryptography and in particular cryptanalysis.
Secrecy, though still important, is no longer the sole purpose of cryptology since the advent of public-key cryptography in the 80s. To replace by electronic devices what had historically been done by paperwork, digital signatures and authentication were introduced.
Adjectives often used synonymously are secret, private, and confidential. They all describe information which is not known about by other people or not meant to be known about. Something is
Frequently confused, and misused, terms in cryptology are code and cipher, often employed as though they were synonymous: A code is a rule for replacing one information symbol by another. A cipher likewise, but the rules governing the replacement (the key) are a secret known only to the transmitter and the legitimate recipient.
A codification or an encoding is a rule for replacing one bit of information (for example, a letter) with another one, usually to prepare it for processing by a computer.
encoding: a rule for replacing one bit of information (for example, a letter) with another one, usually to process it by a computer.
For example,
ASCII code) from 1963 that represents on computers
128 characters (and operations such as backspace and
carriage return) by seven-bit numbers, that is, by sequences of seven 1s
and 0s. For example, in ASCII a lowercase a is always
1100001, a lowercase b is always
1100010, and so on (whereas an uppercase A is
always 1000001, an uppercase B is always
1000010).UTF-8 (8-bit Unicode Transformation
Format) is a variable-length character encoding by Ken Thompson and Rob
Pike to represent any universal character in the Unicode standard (which
possibly has up to
billion characters, and includes the alphabets of many languages, such
as English, Chinese, …, as well as meaningful symbols such as emoticons)
by a sequence of between 1 up to 4 bytes, and
which is backwards compatible with ASCII , and is becoming
the de facto standard.A cipher, like an encoding, also replaces information (which may be anything from a single bit to an entire sequence of symbols) with another one. However, the replacement is made according to a rule defined by a key so that anyone without its knowledge cannot invert the replacement.
cipher: a rule for replacing information (for example, a text) so that its inverse is only feasible by knowledge of the key.
Information is frequently both encoded and enciphered: For example, a
text is encoded, for example, by ASCII, and then encrypted, for example,
by the Advanced Encryption Standard (AES).
Please distinguish between cryptology, cryptography and cryptanalysis:
Please distinguish between encoding and encryption:
While both encoding and encryption transform information into a computer readable format, only for encryption this transformation is not invertible without knowledge of the key.
A snappy acronym to resume the fundamental aims of information
security is the CIA, which stands for:
Confidentiality, Integrity and
Availability. That is, confidentiality of information,
integrity of information and availability of information.
CIA: stands for
Confidentiality,Integrity andAvailability.
More comprehensive are “the five pillars of Information Assurance”, that add authentication and non-repudiation: Confidentiality, integrity, availability, authentication and non-repudiation of information.
The five pillars of Information Assurance: are formed by Confidentiality, integrity, availability, authentication and non-repudiation of information.
Cryptography helps to achieve all of these to good effect: Good
encryption, as achieved by thoroughly tested standard algorithms such as
AES or RSA, is practically impossible to break
computationally; instead, keys are stolen or plaintext is stolen before
encryption or after decryption. While cryptography provides high
technical security, human failure, for example, arising out of
convenience or undue trust, is the weakest point in information
security.
Information that is confidential is meant to be kept secret,
that is, should not be disclosed to other people, for example
information that is known only by someone’s doctor or bank. In law,
confidential is the relation existing between, for example, a client and
her counsel or agent, regarding the trust placed in one by the other. In
the information security standard ISO/IEC 27002 the
International Organization for Standardization (ISO) defines
confidentiality as “ensuring that information is accessible
only to those authorized to have access”. In IT, it means ensuring that
sensitive information stored on computers is not disclosed to
unauthorized persons, programs or devices. For example, avoiding that
anyone with access to a network can use common tools to eavesdrop on
traffic and intercept valuable private information.
Integrity is the state of being whole, the condition of being unified or sound in construction.
(Data) Integrity is about the reliable, complete and error-free, transmission and reception or storage of data: that the original data had not been altered or corrupted; in particular, is valid in accordance with expectations.
When the data has been altered, either through electronic damage by software or physical damage to the disk, the data is unreadable. For example when we download a file we verify its integrity by calculating its hash and comparing with the hash published by source. Without such a check, someone could, for example, package a Trojan horse into an installer on Microsoft Windows (that, as a last resort, hopefully would already be known and detected by an antivirus program such as Microsoft Defender).
Though unrelated to cryptology, in IT security availability of information against threats such as DoS (Denial of Service) attacks (to deny users of the Website access to a Website by flooding it with requests) or accidents, such as power outages, or natural disasters such as earthquakes. To achieve it, it is best to have a safety margin and include redundancy, in particular, to have
Authentic (from Greek authentes, real or genuine) means according to Webster (1913)
Authentication thus is the verification of something (or someone) as “authentic”. This might involve confirming the identity of a person or the origins of an object.
In IT, authentication means
To verify her identity, a person proves that she is who she claims to be by showing some evidence. Devices that are used for authentication include passwords, personal identification numbers, smart cards, and biometric identification systems. For example, to login, she enters her user identification and password.
A common attack is that of the “man in the middle”, where the attacker assumes to either correspondent the identity of the other correspondent. To solve this, certificates, digital signatures by third parties, are used. Either,
OpenPGP, by signatures among
persons known to each other over ends, orVeriSign.Repudiation is a legal term for disavowal of a legal bind (such as an agreement or obligation); someone who repudiates:
For example, a forged or forced signature is repudiable.
Non-repudiation is the assurance:
In computing, this means that authentication can hardly be refuted afterwards. This is achieved by a digital signature.
For example,
In today’s global economy, where face-to-face agreements are often impossible, non-repudiation is essential for safe commerce.
In practice, is sensitive information obtained by
failure?
What does CIA in IT security stand for: Confidentiality, Integrity and Availability.
Please list the five pillars of information security: Confidentiality, integrity, availability, authentication and non-repudiation of information.
Alice wants to send Bob a locked box (with a message or a key) without sending the key, so that the box was never left unlocked throughout the process.
An open lock is the public key and locking its application. The key is the secret key:
The key or message in the box is the shared secret. The other two keys the mutual secrets. From two two-sided one can be constructed by the interchangeability of the order of the encryptions, commutativity.
The history of cryptography dates back at least 4000
years. We distinguish three periods:
Till the 20th century, its methods were classic, mainly pen and paper.
In the early 20th century, they were replaced by more efficient and sophisticated methods by complex electromechanical machines, mainly rotor machines for polyalphabetic substitution, such as the Enigma rotor machine used by the axis powers during World War II.
Since then, digitalization, the replacement of analog devices by digital computers, allowed methods of ever greater complexity. Namely, the most tested algorithms are
DES (or its threefold iteration 3DES) and
its successor AES for symmetric cryptography,RSA and its successor ECC (Elliptic Curve
Cryptography) for asymmetric cryptography.From antiquity till World War I, cryptography was carried out by hand and thus limited in complexity and extent to at most a few pages. The principles of cryptanalysis were known, but the security that could be practically achieved was limited without automatization. Therefore, given sufficient ciphertext and effort, cryptanalysis was practically always successful.
The principles of cryptanalysis were first understood by the Arabs. They used both substitution and transposition ciphers, and knew both letter frequency distributions and probable plaintext in cryptanalysis. Around 1412, al-Kalka-shandī gave in his encyclopedia Subīal-aīshī a manual on how to cryptanalyze ciphertext using letter frequency counts with lengthy examples.
A scytale (from Latin scytala) consists of a rod with a band of parchment wound around it on which is written a secret message. It was rolled spirally upon a rod, and then written upon. The secret writing on the strip wound around the rod is only readable if the parchment was to be wound on a rod of the same thickness; It is a transposition cipher, that is, shuffles, or transposes, the letters of the plaintext.
Caesar’s Cipher is one of the simplest and most widely-known chiphers, named after Julius Caesar (100 – 44 BC), who used it to communicate with his generals. It is a substitution cipher that replaces, substitutes, each alphabetic letter of the plaintext by a fixed alphabetic letter. In Caesar’s Cipher, each letter in the plaintext is shifted through the alphabet the same number of positions; that is, each letter in the plaintext is replaced by a letter some fixed number of positions further down the alphabet.
Francis Bacon’s cipher from 1605 is an arrangement of the letters
a and b in five-letter combinations (of which
there are
) that each represent a letter of the alphabet (of which there are
26 ). Nowadays we would call a code, but at the time it
illustrated the important principle that only two different signs can be
used to transmit any information.
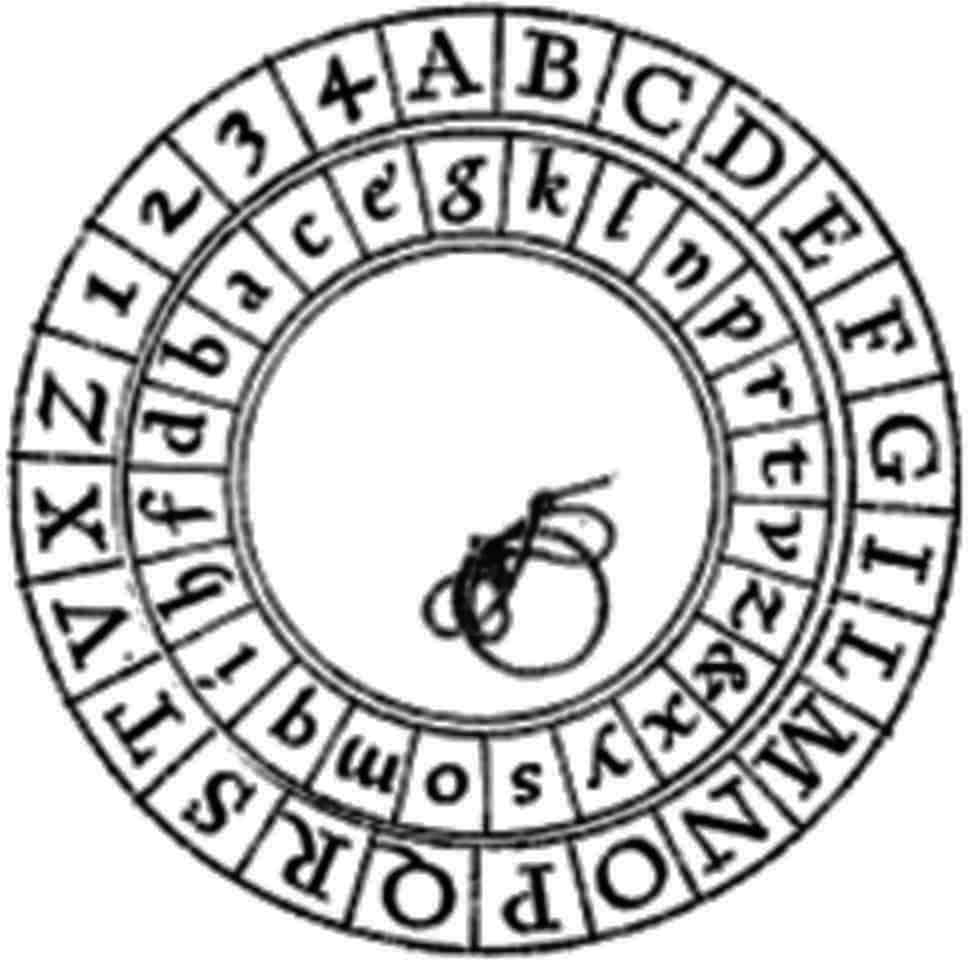
In 1470, Leon Battista Alberti described in Trattati in Cifra (“Treatise on Ciphers”) the first cipher disk to shift the letters of the alphabet cyclically. He recommended changing the offset after every three or four words, thus conceiving a polyalphabetic cipher in which the same alphabetic letters are replaced by different ones. The same device was used more than four centuries later by the U.S. Army in World War I.

The best known cipher of World War I is the German
ADFGVX cipher:
A, D,
F, G, V, and X.Invented by Fritz Nebel, it was introduced in March 1918 for use by mobile units. The French Bureau du Chiffre, in particular, Georges Painvin, broke the cipher a month later — still too late as the German attacks had already ceded.
The mechanization of cryptography began after World War I by the development of so-called rotor cipher machines:

These rotors are stacked. The rotation of one rotor causes the next one to rotate of a full revolution. (Just like in an odometer where after a wheel has completed a full revolution, the next one advances of a full revolution.) In operation, there is an electrical path through all rotors. Closing the key contact of the plaintext letter on a typewriter-like keyboard
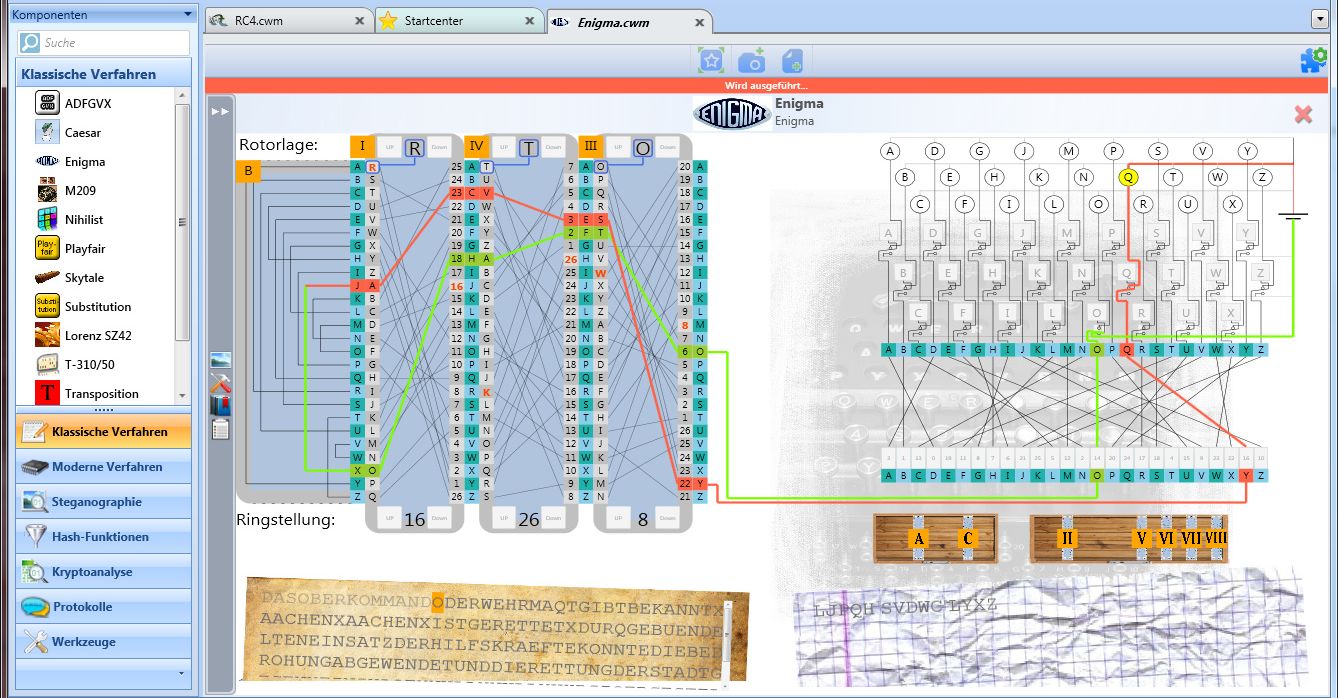
In the US, Edward H. Hebern made in 1917 the first patent claim to accomplish polyalphabetic substitution by cascading a collection of monoalphabetic substitution rotors, wiring the output of the first rotor to the input of the following rotor, and so on. In Europe, Already in 1915 such a rotor machine had been built by two Dutch naval officers, Lieut. R.P.C. Spengler and Lieut. Theo van Hengel, and independently by a Dutch mechanical engineer and wireless operator, Lieut. W.K. Maurits. Around the same time as Hebern, Arthur Scherbius from Germany (who filed his patent in February 1918) and Hugo A. Koch from the Netherlands (a year later), also built rotor machines, which were commercialized and evolved into the German Enigma used in World War II.
In Japan, the Japanese Foreign Office put into service its first rotor machine in 1930, which was cryptanalyzed in 1936, using solely the ciphertexts, by the U.S. Army’s Signal Intelligence Service (SIS). (In 1939 a new cipher machine was introduced, in which rotors were replaced by telephone stepping switches, but readily broken by the SIS again solely relying on ciphertext; even more so, their keys could be foreseen.)
Arthur Scherbius was born in Frankfurt am Main on 20 October 1878 as son of a businessman. After studying at the Technical College in Munich, he completed his doctoral dissertation at the Technical College in Hanover in 1903, then worked for several major electrical companies in Germany and Switzerland. In 1918, he submitted a patent for a cipher machine based on rotating wired wheels and founded his own firm, Scherbius and Ritter. Since both the imperial navy and the Foreign Office declined interest, he entered the commercial market in 1923 and advertised the Enigma machine, as it was now called, in trade publications or at the congress of the International Postal Union. This sparked again the interest of the German navy in the need for a secure cipher, and a slightly changed version was in production by 1925. Still, the corporation continued to struggle for profitability because commercial as public demand was confined to a few hundred machines. While Scherbius fell victim to a fatal accident involving his horse-drawn carriage, and died in 1929, his corporation survived and by 1935 amply supplied the German forces under Hitler’s rearmament program.
Polish and British cryptanalysis solved the German Enigma cipher (as well as two telegraph ciphers, Lorenz-Schlüsselmaschine and Siemens & Halske T52). To this end
Hans-Thilo Schmidt, decorated with an Iron Cross in World War I, worked as a clerk at a cipher office (previously lead by his brother). In June 1931, he contacted the intelligence officer at the French embassy and agreed with Rodolphe Lemoine to reveal information about the Enigma machine, copies of the instruction manual, operating procedures and lists of the key settings. However, French cryptanalysts made little headway, and the material was passed on to Great Britain and Poland, whose specialists had more success:
The commercial version of the Enigma had a rotor at the entry and his wiring was unknown. However, the Polish cryptanalyst Marian Rejweski, guided by the German inclination for order, found out that it did not exist in the military version; what is more, he inferred the internal wirings of the cylinders by distance, that is, by mere cryptanalysis of the enciphered messages.

The Britisch cryptanalysts in Bletchley Park (among them the
mathematician Alan Turing, a founding father of theoretical computer
science) could reduce by likely candidates the number of possible keys
from 150 trillions to around a million, a number that
allowed a work force of around 4200 (among them
women) an exhaustive key-search with the help of the Turing Bomb, an
ingenious electromechanical code-breaking machine that imitated a
simultaneous run of many Enigma machines and efficiently checked the
likelihood of their results.

Schmidt continued to inform the Allies throughout war till the arrest (and confession) of Lemoine in Paris which lead to that of Schmidt by the Gestapo in Berlin on 1 April 1943 and his death in prison.
After World War II, cryptographic machines stayed conceptually the same till the early 80s: faster rotor machines in which rotors had been replaced by electronic substitutions, but still merely concatenating shifted monoalphabetic substitutions to obtain a polyalphabetic substitution.
However, such letter per letter substitutions are still linear over the letters, so the ciphertext obtained from a plaintext will reveal how to decrypt all letters of a plaintext of (at most) the same length. That is, a letter per letter substitution diffuses little, that is, hardly spreads out changes; optimal diffusion is attained whenever the change of a single letter of the plaintext causes the change of half of the letters of the ciphertext. If the attacker has access to the ciphertexts of many plaintexts, possibly of his own choosing, then he can obtain the key by the ciphertexts of two plaintexts that differ in a single position.
Instead, computers made it possible to combine such substitutions
(such as Caesar’s Cipher) with transpositions (such as the Scytale),
achieving far better diffusion, which lead to the creation of one of the
most widely used ciphers in history, the Data Encryption Standard
(DES), in 1976.
In January 1997 the U.S. National Institute of Standards and
Technology (NIST; former National Bureau of Standards, NBS) announced a
public contest for a replacement of the aging DES, the
Advanced Encryption Standard (AES). Among 15 viable
candidates from 12 countries, in October 2000 Rijndael, created by two
Belgian cryptographers, Joan Daemen and Vincent Rijmen, was chosen and
became the AES.
Since improvements in computing power allowed to find the fixed
56-bit DES key by exhaustive key-search (brute force), the
NIST specifications for the AES demanded an increasing key length, if
need be. Rijndael not only was shown immune to the most sophisticated
known attacks such as differential cryptanalysis (in Daemen and Rijmen
(1999) and Daemen and Rijmen (2002)) and of an elegant and simple
design, but is also both small enough to be implemented on smart cards
(at less than 10 000 bytes of code) and flexible enough to
allow longer key lengths.
Since the ’80s, the advent of public-key cryptography in the information age made digital signatures and authentication possible; giving way to electronic information slowly replacing graspable documents.
Asymmetric encryption was first suggested publicly at Diffie and Hellman (1976).
Conceptually it relies on a trap function (more specifically, in op.cit. the modular exponential), an invertible function that is easily computable but whose inverse is hardly computable in the absence of additional information, the secret key.
To encrypt, the function is applied; to decrypt its inverse with the secret key. For example, in the approach according to Diffie and Hellman, this function is the exponential, however, over a different domain than the real numbers we are used to.
In fact, Diffie and Hellman (1976) introduced only a scheme for exchanging a secret key through an insecure channel. It was first put it into practice
RSA
cryptographic algorithm was introduced, orElGamal algorithm, more recent, but the closest
example of the original scheme.Not only do these algorithms enable ciphering by a public key (thus removing the problem of its secret communication), but, by using the private key instead to encipher, made possible digital signatures, which might have been its commercial breakthrough. These algorithms still stand strong, but others, such as elliptic curve cryptography, are nowadays deemed more efficient at the same security.
26
including the trivial one.Kerckhoff principle postulates the independence of a cryptographic algorithm’s security from its secrecy:
Kerckhoffs’ principle: The ciphertext should be secure even if everything about it, except the key, is public knowledge.
While knowledge of the key compromises a single encryption, knowledge of the algorithm will compromise all encryptions ever carried out. A public algorithm guarantees the difficulty of decryption depending only on the knowledge of the key, but not on the algorithm. The more it is used, the more likely it becomes that the algorithm will be eventually known. For the algorithm to be useful, it thus needs to be safe even though it is public.
Claude Shannon (1916 – 2001) paraphrased it as: “the enemy knows the system”, Shannon’s maxim. The opposite would be to rely on a potentially weak, but unknown algorithm, “security through obscurity”; ample historic evidence shows the futility of such a proposition (for example, the above ADFGVX cipher of Section 1.4 comes to mind).
Shannon’s principles of
give criteria for an uninferable relation between the ciphertext and
Ideally, when one letter in the key respectively in the plaintext changes, then half of the ciphertext changes, that is, each letter in the ciphertext changes with a probability of 50%. While the output of the cipher, the ciphertext, depends deterministically on the input, the plaintext, and the key, the algorithm aims to obfuscate this relationship to make it as complicated, intertwined, scrambled as possible: each letter of the output, of the ciphertext, depends on each letter of the input, of the plaintext, and of the key.
DES and AES.Cryptography protects information by shuffling data (that is, transforming it from intelligible into indecipherable data) so that only additional secret information, the key, can feasibly reverse it. Up to the end of the ’70s, the key used to encrypt and decrypt was always the same: symmetric or (single-key) cryptography. In the 70s asymmetric cryptography was invented, in which the key to encipher (the public key) and the key to decipher (the secret or private key) are different. In fact, only the key to decipher is private, kept secret, while the key to encrypt is public, known to everyone. When the keys exchange their roles, the private key enciphers, and the public one deciphers, then the encryption is a digital signature. while the encrypted message will no longer be secret, every owner of the public key can check whether the original message was encrypted by the private key. Because historically only written messages were encrypted, the source data, though a stream of 1s and 0s (the viewpoint adopted in symmetric cryptography) or a number (that adopted in asymmetric cryptography), is called plaintext and the encrypted data the ciphertext.
The security
RSA , requires the factorization of a
number with
decimal digits into its prime factors, which is computationally
infeasible (without knowledge of the key);Good encryption, as achieved by standard algorithms such as
AES or RSA, is practically impossible to break
computationally; instead, keys are stolen or plaintext is stolen before
encryption or after decryption.
A hash function is an algorithm that generates an output of fixed
(byte) size (usually around 16 to 64 bytes)
from an input of variable (byte) size, for example, a text or image
file, a compressed archive. The output string of fixed length that a
cryptographic hash function produces from a string of any length (an
important message, say) is a kind of inimitable “signature”. A person
who knows the “hash value” cannot know the original message, but only
the person who knows the original message can prove that the “hash
value” is produced from that message.
The article Simmons et al. (2016) gives a good summary of cryptology, in particular, historically; read its introduction and the section on history. As does the first chapter of Menezes, Oorschot, and Vanstone (1997), which focuses more on the techniques. The most recent work is Aumasson (2017), and a concise but demanding overflight of modern cryptography. Get started by reading its first chapter as well.
Some classics are Frederick) Friedman (1976) which is a manual for cryptanalysis for the U.S. military, originally not intended for publication.
The books Kahn (1996) and Singh (2000) trace out the history of cryptanalysis in an entertaining way.
The book Schneier (2007) is a classic for anyone interested in understanding and implementing modern cryptographic algorithms.
On completion of this chapter, you will have learned …
… that the two fundamental symmetric cryptographic algorithms are
… that the only cryptographically perfectly secure cipher is the one-time pad in which the key is as long as the plaintext
… that modern algorithms like DES and
AES are Substitution and Permutation Networks that
break the plaintext up into short blocks of the same size as the key
and, on each block, iterate
Up to the end of the ’70s, before the publication of Diffie and Hellman (1976) and Rivest, Shamir, and Adleman (1978), all (known) cryptographic algorithms were symmetric (or single-key), that is, used the same key to encipher and decipher. Thus every historic algorithm, as sophisticated as it may be, be it Caesar’s Cipher, the Scytale or the Enigma, was symmetric.
While asymmetric algorithms depend on a computationally difficult problem, such as the factorization of a composed number into its prime factors, and regard the input as a natural number, symmetric ones operate on the input as a string (of bits or letters) by (iterated) substitutions and transpositions.
The only perfectly secure cipher is the one-time pad in which the key is as long as the plaintext and the ciphertext is obtained by adding, letter by letter, each letter of the key to the corresponding (that is, at the same position) letter of the plaintext.
However, such a large key is impractical for more complex messages, such as text, image or video files: In modern times, it means that to encrypt a hard drive, another hard drive that carries the key is needed.
To compensate the shorter key length, modern algorithms, ideally,
create so much intertwining that they achieve almost perfect
diffusion, that is, the change of a single bit of the input or key
causes the change of around half of the output bits. Modern algorithms,
such as DES or AES, are substitution and
permutation network block ciphers, meaning that they encrypt one chunk
of data at a time by iterated transpositions and substitutions.
The two basic operations to encrypt are transposition and substitution:
The historical prototypical algorithms for these two operations are:
A as
D, B as E, and so forth, andWe will see that even with many possible keys an algorithm, such as that given by any permutation of the alphabet which has almost keys, can be easily broken if it preserves regularities, like the frequency of the letters.
As a criterion for security, there is that of diffusion by Shannon: Ideally, if a letter in the plaintext changes, then half of the letters in the ciphertext changes. Section 2.2 will show how modern algorithms, called substitution and permutation networks, join and iterate these two complementary prototypical algorithms to reach this goal.
ideal diffusion (according to Shannon): if a bit in the plaintext or key changes, then half of the bits in the ciphertext changes.
In a substitution cipher the key determines substitutions of the plaintext alphabet (considered as a set of units of symbols such as single letters or pairs of letters) by the ciphertext alphabet. For example, if the units of the plaintext and ciphertext are both the letters of the Latin alphabet, then a substitution permutes the letters of the Latin alphabet. If the substitution cipher is monoalphabetic (such as Caesar’s Cipher), then the same substitution is applied to every letter of the plaintext independent of its position. If the substitution cipher is polyalphabetic (such as the Enigma), then the substitution varies with the position of the letter in the plaintext. To encrypt, each alphabetical unit of the plaintext is replaced by the substituted alphabetical unit, and inversely to decrypt.
Substitution Cipher: a cipher that replaces each alphabetical unit of the plaintext by a corresponding alphabetical unit.
Every monoalphabetic substitution cipher, that is,
every plaintext symbol is always encrypted into the same ciphertext
symbol, is insecure: the frequency distributions of symbols in the
plaintext and in the ciphertext are identical, only the symbols having
been relabeled. Therefore, for example in English, around
25 letters of ciphertext suffice for cryptanalysis.
The main approach to reduce the preservation of the single-letter frequencies in the ciphertext is to use several cipher alphabets, that is, polyalphabetic substitution.
The simplest substitution cipher is a cyclical shift of the plaintext alphabet; Caesar’s cipher.
Caesar’s Cipher A substitution cipher that shifts the alphabetical position of every plaintext letter by the same distance.
This method was used by Roman emperors Caesar (100 – 44 B.C.) and Augustus (63 – 14 B.C.): fix a distance between letters in alphabetical order, that is, a number between 0 and 25, and shift (forward) each letter of the (latin) alphabet by this distance . We imagine that the alphabet is circular, that is, that the letters are arranged in a ring, so that the shift of a letter at the end of the alphabet results in a letter at the beginning of the alphabet.

For example, if , then
There are 26 keys (including the trivial key
).

To decipher, each letter is shifted by the negative distance , that is, positions backwards. If the letters of the alphabet form a wheel, then the letters are transferred
By the cyclicity of the letter arrangement, we observe that a transfer of positions in counterclockwise direction equals one of positions in clockwise direction.
Instead of replacing each letter by one shifted by the same distance , let us replace each letter with some letter, for example:
| A | B | … | Y | Z |
| ↓ | ↓ | … | ↓ | ↓ |
| E | Z | … | G | A |
To revert the encipherment, never two letters be sent to the same
letter! That is, we shuffle the letters among themselves. This way we
obtain
keys (which is around the number of passwords with 80
bits).
A transposition (or permutation) cipher encrypts the plaintext by permuting its units (and decrypts by the inverse permutation). Each alphabetical unit stays the same; the encryption depends only on the positions of the units.
Transposition Cipher: Transpose the alphabetical units of the plaintext.
The Scytale or Licurgo’s Baton (= a Spartan legislator around 800 B.C.) is a cipher used by the Spartans, as follows:
The letters thus transposed on the strip could only be deciphered by a stick with the same circumference (and being long enough) in the same way as the text was encrypted:
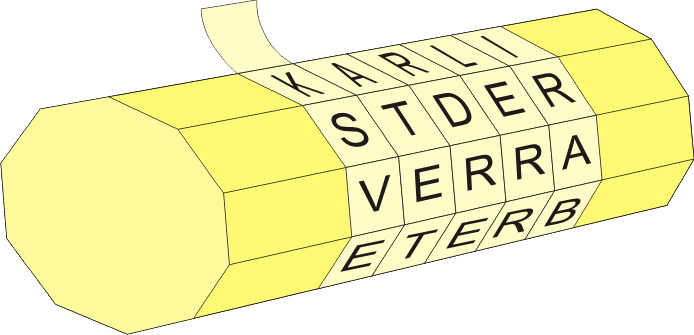
Here, the key is given by the stick’s circumference, that is, the number of letters that fit around the stick.
For example, if the stick has a circumference of 2
letters (and a length of 3 letters), the two rows
| B | I | G |
| S | U | M |
become the three rows
| B | S |
| I | U |
| G | M |
which, once concatenated (to reveal neither the circumference nor the length), become
| B | S | I | U | G | M |
Let us apply the established security criteria to the substitution ciphers:
This simple substitution cipher violates all desirable qualities: For example, Kerckhoff’s principle that the algorithm be public: Once the method is known, considering the small amount of 25 keys, the ciphertext gives way in short time to a brute-force attack:
brute-force attack: an exhaustive key-search that checks each possible key.
A substitution by any permutation of the letters of the alphabet, such as,
| A | B | … | Y | Z |
| ↓ | ↓ | … | ↓ | ↓ |
| E | Z | … | G | A |
has keys, so a brute-force attack is computationally infeasible.
But it violates the goals of diffusion and confusion. If the key (= permutation of the alphabet) exchanges the letter for the letter , then there’s
In fact, the algorithm allows statistical attacks on the frequency of letters, bigrams (= pairs of letters) and trigrams (= triples of letters). See Section 12.1.
Also the scytale is weak in any sense given by the security principles. It violates
In fact, the maximum value of the circumference of the stick in letters is where = the number of letters in the ciphertext. So a brute-force attack is feasible.
It has
In fact, the algorithm is prone to statistical attacks on the
frequency of bigrams (= pairs of letters), trigrams (= triples of
letters), and higher tuples. For example, a promising try would be the
choice of circumference as number
that maximizes the frequency of the ‘th’ bigram between the
letter strings at positions
,
. For example, if we look
we notice that T and
H are one letter apart, which leads us to the guess that
the circumference is three letters,
, yielding the decipherment
A product cipher composes ciphers, that is, if the product is two-fold, then the output of one cipher is the input of the other.
product cipher: a composition of ciphers where the output of one cipher serves as the input of the next.
The ciphertext of the product cipher is the ciphertext of the final cipher. Combining transpositions only with transpositions or substitutions only with substitutions, the obtained cipher is again a transposition or substitution, and hardly more secure. However, mixing them, a transposition with substitutions, indeed can make the cipher more secure.
A fractionation cipher is a product cipher that:
The most famous fractionation cipher was the ADFGVX
cipher used by the German forces during World War I:
| A | D | F | G | V | X | |
|---|---|---|---|---|---|---|
| A | a | b | c | d | e | f |
| D | g | h | i | j | k | l |
| F | m | n | o | p | q | r |
| G | s | t | u | v | w | x |
| V | y | z | 0 | 1 | 2 | 3 |
| X | 4 | 5 | 6 | 7 | 8 | 9 |
A ,
D , F , G , V , and
X that indicate the row and column of the letter or
digit.However, it was cryptanalyzed within a month by the French cryptanalyst Georges J. Painvin in 1918 when the German army entered in Paris. We will see in Section 2.2 how modern ciphers refine this idea of a product cipher to obtain good diffusion.
Classic ciphers usually replaced single letters, sometimes pairs of letters. Systems that operated on trigrams or larger groups of letters were regarded as too tedious and never widely used.
Instead, it is safer to substitute a whole block (of letters instead
of a single letter, say) according to the key. However, the alphabet of
this replacement would be gigantic, so this ideal is practically
unattainable, especially on hardware as limited as a smart card with an
8 bit processor. For a block of, for example,
bytes, this substitution table would already have a
gigabytes (=
bytes). However, in modern single-key cryptography a block of
information commonly has
bytes, about 27 alphabetic characters (whereas two-key cryptography
based on the RSA algorithm commonly uses blocks of
bits, about
alphabetic characters).
Instead, for example, AES only replaces each byte, each
entry in a block, a replacement table of
entries of
byte (and afterwards transposes the entries.) We will see that these
operations complement each other so well that they are practically as
safe as a substitution of the whole block.
A block cipher partitions the plaintext into blocks
of the same size and enciphers each block by a common key: While a block
could consist of a single symbol, normally it is larger. For example, in
the Data Encryption Standard the block size is 64 bits and
in the Advanced Encryption Standard 128 bits.
stream cipher versus block cipher: a stream cipher operates on single characters (for example, single bytes) while a block cipher operates on groups of characters (for example, each
16bytes large)
A stream cipher partitions the plaintext into units,
normally of a single character, and then encrypts the
-th unit of the plaintext with the
-th unit of a key stream. Examples are the one-time pad, rotor machines
(such as the Enigma) and DES used in Triple
DES (in which the output from one encryption is the input
of the next encryption).
In a stream cipher, the same section of the key stream that was used to encipher must be used to decipher. Thus, the sender’s and recipient’s key stream must be synchronized initially and constantly thereafter.
A Feistel Cipher (after Horst Feistel, the inventor
of DES) or a substitution and permutation
network (SPN ) groups the text (= byte sequence)
into
-byte blocks (for example,
for AES and enciphers each block by iteration (for example,
10 times in AES , and 5 times in
our prototypical model) of the following three steps, in given
order:
XOR) the key,Substitution and Permutation Network: a cipher that iteratively substitutes and permutes each block after adding a key.
That is, after
One-time pad,are applied
AES algorithm (each byte, pair of hexadecimal letters, by
another), andAES , that groups the text
into a
square (whose entries are pairs of hexadecimal letters), the entries in
each row (and the columns) are permuted.These two simple operations,
complement each other well, that is, they generate high confusion and diffusion after a few iterations. In the first and last round, the steps before respectively after the addition of the key are omitted because they do not increase the cryptographic security: Since the algorithm is public (according to Kerckhoff’s principle), any attacker is capable of undoing all those steps that do not require knowledge of the key.
Though seemingly a Feistel Cipher differs from classical ciphers, it is after all a product cipher, made up of transpositions and substitutions.
The Data Encryption Standard (DES), was made a public standard in 1977 after it won public competition announced by the U.S. National Bureau of Standards (NBS; now the National Institute of Standards and Technology, NIST). IBM (International Business Machines Corporation) submitted the patented Lucifer algorithm invented by one of the company’s researchers, Horst Feistel, a few years earlier (after whom the substitution and permutation network was labelled Feistel Cipher). Its internal functions were slightly altered by the NSA (and National Security Agency) and the (effective) key size shortened from 112 bits to 56 bits, before it became officially the new Data Encryption Standard.
DES: Block cipher with an effective key length of
56bits conceived by Horst Feistel from IBM that won a U.S. National competition to become a cryptographic standard in 1977.
DES is a product block cipher of 16 iterations, or
rounds, of substitution and transposition (permutation). Its block size
and key size is 64 bits. However, only 56 of the key bits can be chosen;
the remaining eight are redundant parity check bits.
As the name of its inventor Horst Feistel suggests, it is a Feistel
Cipher, or substitution and permutation network, similar to the
prototype discussed above. It groups the text (= byte sequence) into
32-bit blocks with sub-blocks of 4 bits and
enciphers each block in 16 iterations of the following
three steps, called the Feistel function, for short
F-function, in given order:
add (XOR) the key,
substitution of each 4-bit sub-blocks of the block
by the S-box (in hexadecimal notation), and
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 4 | D | 1 | 2 | F | B | 8 | 3 | A | 6 | C | 5 | 9 | 0 | 7 |
permutation of all the sub-blocks.
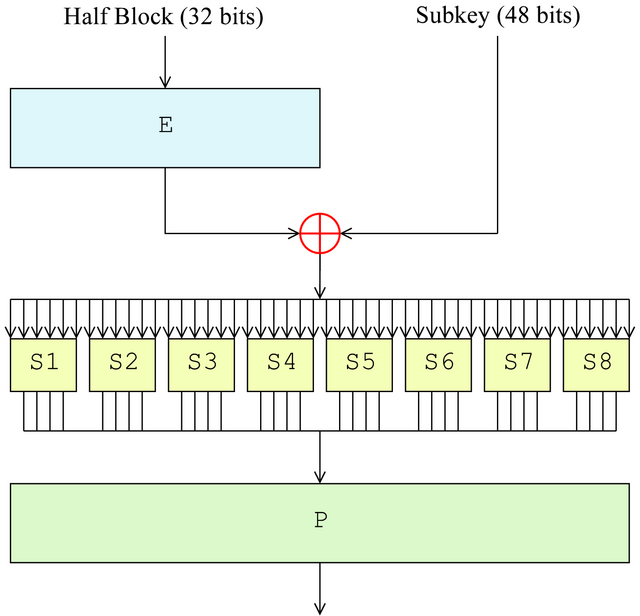
At each round , the output from the preceding round is split into the 32 left-most bits, , and the 32 right-most bits, . will become , whereas is the output of a complex function, whose input is
This process is repeated 16 times.
Essential for the security of DES is the non-linear
S-box of the F -function
specified by the Bureau of Standards; it is not only non-linear, that
is,
but maximizes confusion and diffusion as identified by Claude Shannon
for a secure cipher in Section 2.1.
The security of the DES like any algorithm is no greater
than the effort to search
keys. When introduced in 1977, this was considered an infeasible
computational task, but already in 1999 a special-purpose computer
achieved this in three days. A workaround, called “Triple
DES” or 3DES, was devised that effectively
gave the DES a 112-bit key (using two normal
DES keys).
3DES: Triple application of
DESto double the key size of the DES algorithm.
(Which is after all the key size for the algorithm originally proposed by IBM for the Data Encryption Standard.) The encryption would be while decryption would be , that is, the encryption steps are:
while the decryption steps are:
If the two keys coincide, then this cipher becomes an ordinary single-key DES; thus, triple DES is backward compatible with equipment implemented for (single) DES.
DES is the first cryptographic algorithm to fulfill
Kerckhoff’s principle of being public: every detail of its
implementation is published. (Before, for example, the implementation
records of the Japanese and German cipher machines in World War II were
released only half a century after their cryptanalysis.)
Shortly after its introduction as a cryptographic standard, the use
of the DES algorithm was made mandatory for all (electronic) financial
transactions of the U.S. government and banks of the Federal Reserve.
Standards organizations worldwide adopted the DES, turning it into an
international standard for business data security. It only waned slowly
after its successor AES was adopted around 2000 (after its
shortcomings became more and more apparent and could only be worked
around, by provisional means such as 3DES).
What key size does DES use?
Name a cryptographic weakness of DES: Short key length.
What does 3DES stand for? Tripe DES, that is, tripe application of DES.
What key size does 3DES use?
In January 1997 the U.S. National Institute of Standards and
Technology (NIST; former National Bureau of Standards, NBS) announced a
public contest (National
Institute for Standards and Technology (2000)) for an Advanced Encryption
Standard (AES) to replace the former symmetric
encryption standard, the Data Encryption Standard (DES).
Since improvements in computing power allowed to find the fixed 56-bit
DES key by exhaustive key-search (brute force) in a matter of days, the
NIST specifications for the AES demanded an ever
increasable key length, if ever need be. The winner of this competition,
the algorithm that became the AES, was
Rijndael (named after its creators Vincent Rijmen and Joan
Daemen):
Rijndael: 86 positive votes, 10 negative votes.Serpent: 59 votes in favour, 7 against.Twofish: 31 positive, 21 negative votesRC6: 23 positive, 37 negative votesMARS: 13 votes in favour, 84 against.AES: Substitution and Permutation network with a (variable) key length of usually
128bits conceived by Vincent Rijmen and Joan Daemen that won a U.S. National competition to become a cryptographic standard in 2000 and succeedDES.
The creators of AES could demonstrate in Daemen and Rijmen
(1999) that these two operations
complement each other so well that, after several iterations, they
almost compensate for the absence of a replacement of the entire block
by another. For a more detailed source, see Daemen and Rijmen (2002).
As was the case with DES, the AES, decades
after its introduction, still stands strong against any attacks of
cryptanalysis, but foreseeably will not yield to developments in
computing, as happened to the DES, also thanks to its
adjustable key size.
Among the competitors of public contest by the NIST, none of them
stood out for its greater security, but Rijndael for its
simplicity, or clarity, and in particular computational economy in
implementation. Since this algorithm is to be run everywhere, for
example on 8-bit smart card processors (smartcards), the
decision was made in favour of Rijndael.
Rijndael not only was secure, but thanks to its elegant and
simple design, also both small enough to be implemented on smart cards
(at less than 10,000 bytes of code).
To this day, this algorithm remains unbroken and is considered the
safest; there is no need for another standard symmetric cryptographic
algorithm. And indeed, it runs everywhere: For example, to encrypt a
wireless network, a single key is used, so the encryption algorithm is
symmetrical. The safest option, and therefore most recommended, is
AES.
The AES algorithm is a block cipher, that is, it groups
the plaintext (and the keys) into byte blocks of
-byte
rectangles where
Commonly, and for us from now on,
, that is, the rectangle is a
-square
(containing
bytes or, equivalently,
bits). Each entry of the block is a byte (= sequence of eight binary
digits = eight-bit binary number).
On a hexadecimal basis (= whose numbers are 0 –
9, A = 10, B = 11,
C = 12, D = 13, E = 14 and
F = 15), such a square is for example
A1 |
13 |
B1 |
4A |
A3 |
AF |
04 |
1E |
3D |
13 |
C1 |
55 |
B1 |
92 |
83 |
72 |
The AES algorithm enciphers each byte block
iteratively, in a number of rounds
which depends on the number of columns of
:
there are
rounds for
columns,
rounds for
columns and
rounds for
columns. For us, as we assume
columns,
.
The Substitution and Permutation cipher AES operates
repeatedly as follows on each block:
S-box) with
entries of
byte each.XOR in each entry).The first step is a substitution. The second and third step count as a horizontal permutation (of the entries in each row) respectively vertical permutation (of the entries in each column).
CrypTool 1 offers in Menu
Individual Procedures -> Visualization of Algorithms -> AES
Animation entry to see the animation in Figure 2.1 of the rounds, andInspector entry in Figure 2.2 to experiment with the values of plaintext
and key.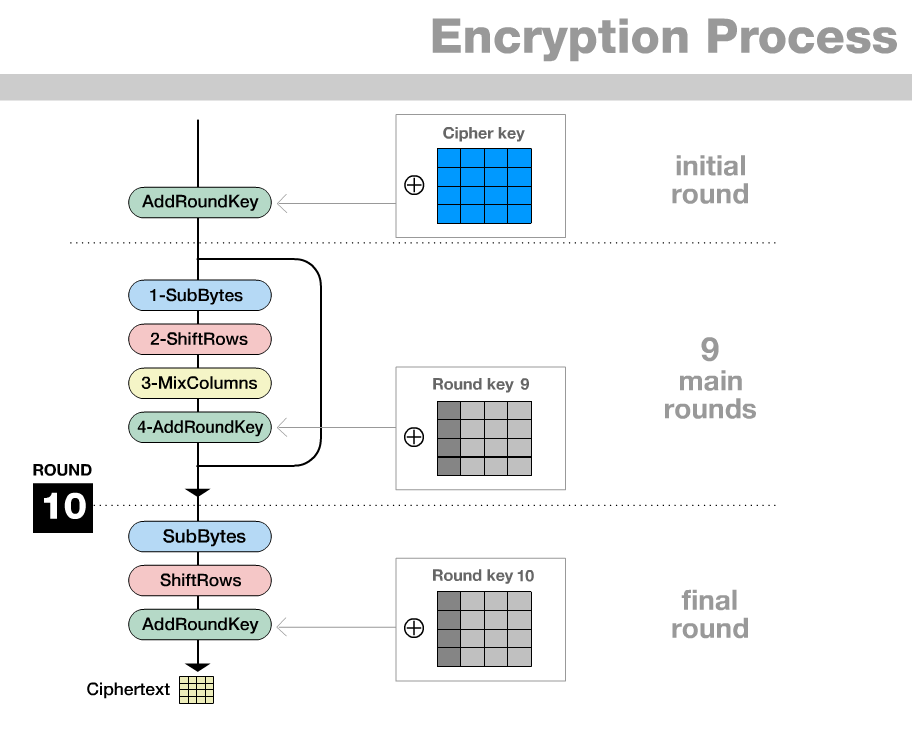
AES rounds in
CrypTool 1 (Zabala (2019a))In these rounds, keys are generated, the plaintext replaced and transposed by the following operations:
Round :
AddRoundKey to add (by XOR) the key to the
plaintext (square) blockRounds : to encrypt, apply the following functions:
SubBytes to replace each entry (= byte = sequence of
eight bits) with a better distributed sequence of bits,ShiftRows to permute the entries of each row of the
block,MixColumn to exchange the entries (= bytes =
eight-digit binary number) of each column of the block by sums of
multiples of them,AddRoundKey to generate a key from the previous round’s
key and add it (by XOR) to the block.Round : to encrypt, apply the following functions:
SubBytesShiftRowsAddRoundKeyThat is, compared to previous rounds, the MixColumn
function is omitted: It turns out that MixColumn and
AddRoundKey, after a slight change of
AddRoundKey, can change the order without changing the end
result of both operations. In this equivalent order, the operation
MixColumn does not increase cryptographic security, as the
last operation invertible without knowledge of the key. So it can be
omitted.
The function MixColumn (and at its origin
SubBytes) uses the multiplication of the so-called
Rijndael field
to compute the multiple of (the eight-digit binary number given by) a
byte; it will be presented at the end of this chapter. Briefly, the
field defines, on all eight-digit binary numbers, an addition given by
XOR and a multiplication given by a polynomial division
with remainder: The eight-digit binary numbers
and
to be multiplied are identified with polynomials
which are then multiplied as usual to
give a polynomial
.
To yield a polynomial with degree
,
the remainder
of
by polynomial division with
is computed. The product
is then given by the coefficients
.
Let us describe all round functions in more detail:
SubBytes substitutes each byte of the block by another
byte given by the S-box substitution table.
To calculate the value of the entry by which the S-box
substitutes each byte:
Calculate its multiplicative inverse in ,
Calculate
where
= 0 , 1 , …, 7 is the index of
each bit of a byte, and
In matrix form, in hexadecimal notation (where the row number corresponds to the first hexadecimal digit and the column number to the second hexadecimal digit of the byte to be replaced):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 63 | 7c | 77 | 7b | f2 | 6b | 6f | c5 | 30 | 01 | 67 | 2b | fe | d7 | ab | 76 |
| 1 | ca | 82 | c9 | 7d | fa | 59 | 47 | f0 | ad | d4 | a2 | af | 9c | a4 | 72 | c0 |
| 2 | b7 | fd | 93 | 26 | 36 | 3f | f7 | cc | 34 | a5 | e5 | f1 | 71 | d8 | 31 | 15 |
| 3 | 04 | c7 | 23 | c3 | 18 | 96 | 05 | 9a | 07 | 12 | 80 | e2 | eb | 27 | b2 | 75 |
| 4 | 09 | 83 | 2c | 1a | 1b | 6e | 5a | a0 | 52 | 3b | d6 | b3 | 29 | e3 | 2f | 84 |
| 5 | 53 | d1 | 00 | ed | 20 | fc | b1 | 5b | 6a | cb | be | 39 | 4a | 4c | 58 | cf |
| 6 | d0 | ef | aa | fb | 43 | 4d | 33 | 85 | 45 | f9 | 02 | 7f | 50 | 3c | 9f | a8 |
| 7 | 51 | a3 | 40 | 8f | 92 | 9d | 38 | f5 | bc | b6 | da | 21 | 10 | ff | f3 | d2 |
| 8 | cd | 0c | 13 | ec | 5f | 97 | 44 | 17 | c4 | a7 | 7e | 3d | 64 | 5d | 19 | 73 |
| 9 | 60 | 81 | 4f | dc | 22 | 2a | 90 | 88 | 46 | ee | b8 | 14 | de | 5e | 0b | db |
| A | e0 | 32 | 3a | 0a | 49 | 06 | 24 | 5c | c2 | d3 | ac | 62 | 91 | 95 | e4 | 79 |
| B | e7 | c8 | 37 | 6d | 8d | d5 | 4e | a9 | 6c | 56 | f4 | ea | 65 | 7a | ae | 08 |
| C | ba | 78 | 25 | 2e | 1c | a6 | b4 | c6 | e8 | dd | 74 | 1f | 4b | bd | 8b | 8a |
| D | 70 | 3e | b5 | 66 | 48 | 03 | f6 | 0e | 61 | 35 | 57 | b9 | 86 | c1 | 1d | 9e |
| E | e1 | f8 | 98 | 11 | 69 | d9 | 8e | 94 | 9b | 1e | 87 | e9 | ce | 55 | 28 | df |
| F | 8c | a1 | 89 | 0d | bf | e6 | 42 | 68 | 41 | 99 | 2d | 0f | b0 | 54 | bb | 16 |
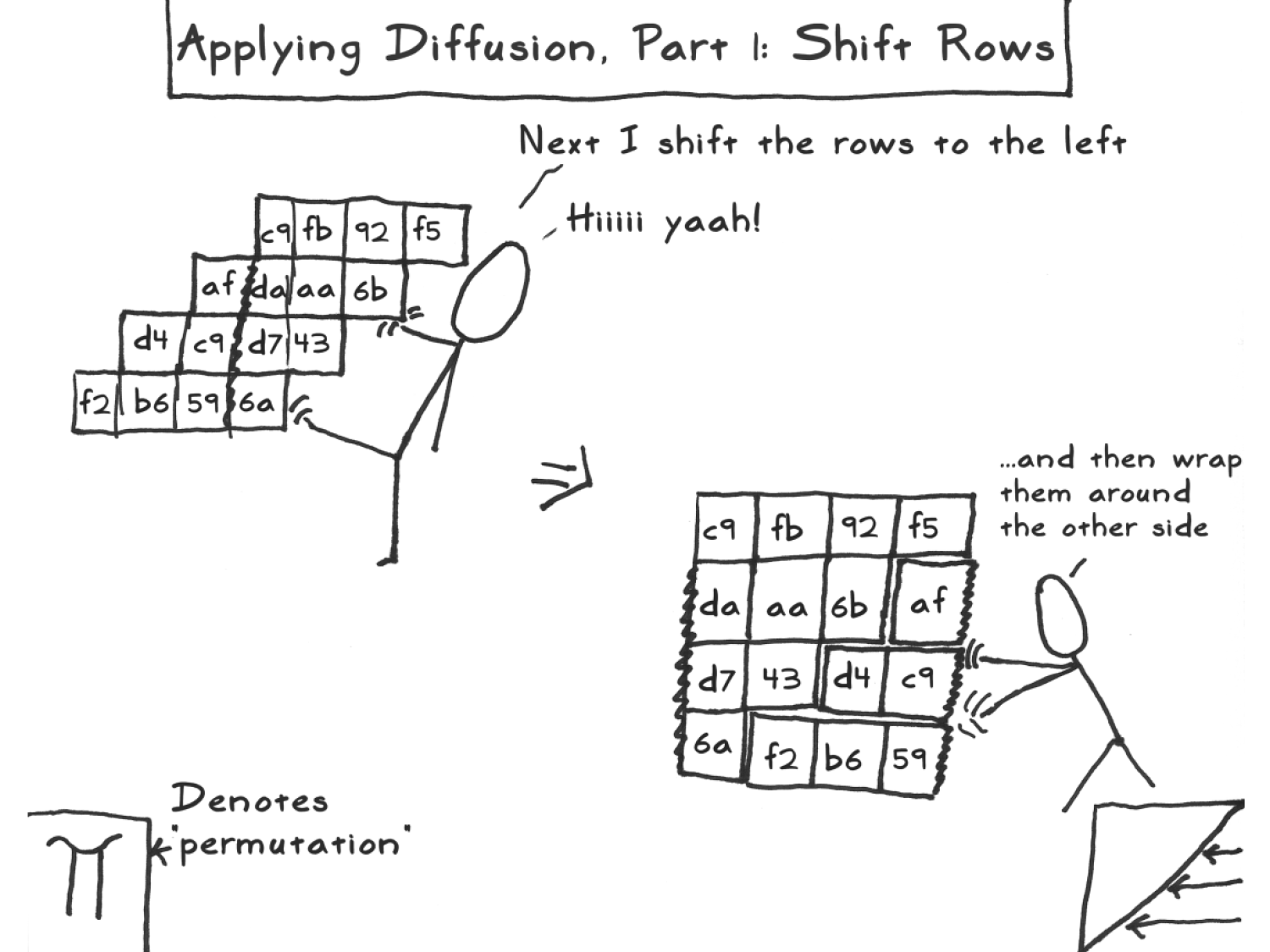
ShiftRows shifts the
-th
row (counted starting from zero, that is,
runs through
,
,
and
;
in particular, the first row is not shifted)
positions to the left (where shift is cyclic). That is, the (square)
block with entries
| B00 | B01 | B02 | B03 |
| B10 | B11 | B12 | B13 |
| B20 | B21 | B22 | B23 |
| B30 | B31 | B32 | B33 |
is transformed into one with entries
| B00 | B01 | B02 | B03 |
| B11 | B12 | B13 | B10 |
| B22 | B23 | B20 | B21 |
| B33 | B30 | B31 | B32 |
MixColumn exchanges all entries of each column of the
block by a sum of multiples of them. This is done by multiplying each
column by a fixed matrix. More exactly,
then For example, the byte is computed by
AddRoundKey adds, by the XOR operation, the
key
of the current round
to the current block
of the ciphertext, the status, that is,
is transformed into
The key is generated column by column.
We denote them by
,
,
and
;
that is,
Since the key has
bytes, each column has
bytes.
ScheduleCore applied
to the first column of the previous round key (which we denote by
); here ScheduleChore is the composition of
transformations:
SubWord : Substitutes each of the 4 bytes
of
according to the S-box of SubBytes .RotWord : Shift
one byte to the left (in a circular manner, that is, the last byte
becomes the first).Rcon(r): Adds (by XOR ) to
the constant value, in hexadecimal notation,
(where the power, that is, the iterated product, is calculated in the
Rijndael field
).
That is, the only byte that changes is the first one, by adding either
the value
(for
) or the value
in
for
.We note that the only transformation that is not affine
(that is, the composition of a linear application and a constant shift)
is the multiplicative inversion in the Rijndael field
in the SubBytes operation. In fact
SubBytes are applied, in this order,
ShiftRows is a permutation, in particular, linear.MixColumn is an addition, in particular, linear.AddRoundKey is the translation by the round key.Regarding the goals of ideal diffusion and
confusion, we can point out that in each step about half of the
bits (in SubBytes) or bytes (in MixColumn and
ShiftRows)is replaced and transposed. To convince oneself
of the complementarity of the simple operations for high security, that
is, that they generate in conjunction high confusion and diffusion after
few iterations:
it is worth to experiment in
Individual Procedures -> Visualization of Algorithms -> AES -> Inspector
with some pathological values, for example:
00, and00 and plaintext entries equals
00 except one entry equals 01, that is, change
a single bit.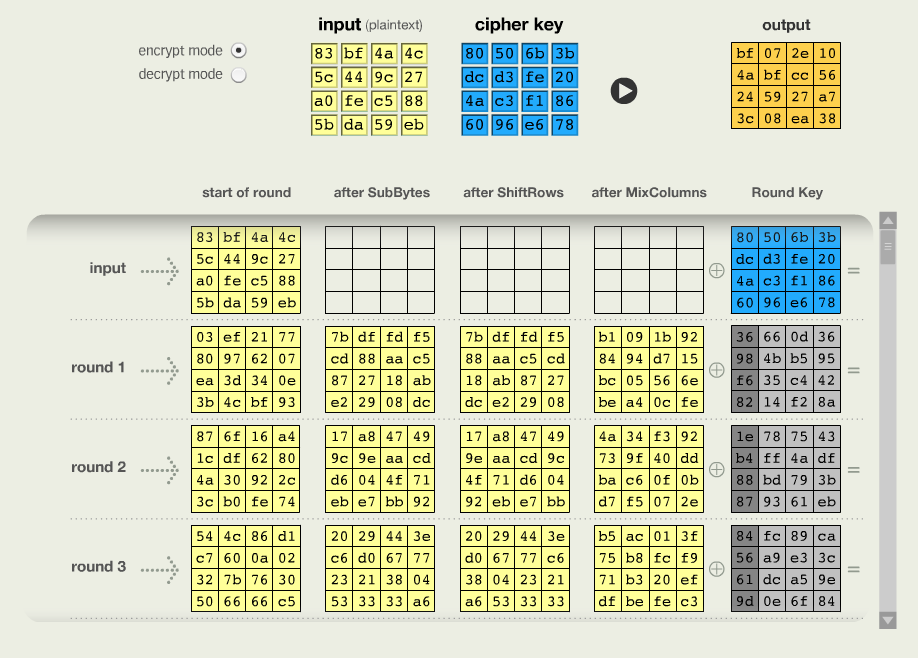
AES in CrypTool 1 (Zabala (2019b))We see how this small initial difference spreads out, already
generating totally different results after, say, four rounds! This makes
plausible the immunity of AES against differential
cryptanalysis.
In case all key and plaintext entries are equal to 00 ,
we also understand the impact of adding the Rcon(r)
constant to the key in each round: that’s where all the confusion comes
from!
The function MixColumn (as well as the computation of
the power of Rcon in AddRoundKey) uses the
multiplication given by the so-called Rijndael field,
denoted
,
to compute the multiple of (the number given by a) byte; let us quickly
introduce it:
A group is a set with
Generally,
Example. The set of nonzero rational numbers with the multiplication operation is a group.
If the group is commutative, that is, if the operation satisfies the commutativity law, then commonly
Example. The set of rational numbers with the addition operation is a commutative group.
A field is a set with an addition and multiplication operation and such that
Example. The set of rational numbers with addition and multiplication is a field.
A byte, a sequence
…
,
of eight bits in
is considered a polynomial with binary coefficients by
For example, the hexadecimal number
, or binary number
, corresponds to the polynomial
All additions and multiplications in
AES take place in the binary field
with
elements, which is a set of numbers with addition and multiplication
that satisfies the associativity, commutativity and distributivity law
(like, for example,
) defined as follows: Let
be the field of two elements
with
XOR ), andLet that is, the finite sums to , , …, to and be That is, the result of both operations and in is the remainder of the division by .
The
addition of two polynomials is the addition in
coefficient to coefficient. That is, as bytes, the
addition is given by the XOR addition.
The multiplication is given by the natural multiplication followed by the division with rest by the polynomial For example, in hexadecimal notation, , because and The multiplication by the polynomial does not change anything, it is the neutral element. For every polynomial , Euclid’s extended algorithm, calculates polynomials and such that That is, in the division with the remaining for left over . This means that is the inverse multiplicative in , When we invert a byte into , we mean byte .
How many rounds has AES for a 128 bit key?
Which are the steps of each round? SubBytes,
ShiftRows, MixColumn and
AddRoundKey
Which one of the steps is non-linear?
SubBytesShiftRowsMixColumnAddRoundKeyThere are two basic operations in ciphering: transpositions and substitution.
Either of these ciphers is insecure because they preserve statistical data of the plaintext: For example, a mere (monoalphabetic) substitution cipher falls victim to the frequency distributions of symbols in the plaintext being carried over to the ciphertext. Instead, a modern cipher combines substitution and permutation ciphers, so called substitution and permutation network or Feistel cipher
While the only cipher proved to be perfectly secure, that is
no method of cryptanalysis is faster than exhaustive key-search, modern
ciphers such as DES from 1976 or AES from 2000
in practice achieve, up to (the k)now, the same, that is, no
cryptanalytic method faster than exhaustive key-search is known. The key
criterion for this feat is high diffusion as defined by
Shannon, that is, if a bit in the plaintext or key changes, then half of
the bits in the ciphertext changes. Compare it to that of ancient
algorithms!
Read the section on symmetric cryptography in the article Simmons et al. (2016).
Read (at least the beginnings of) Chapter 9 on hash
functions in Menezes, Oorschot, and Vanstone (1997), and (at least the beginnings of)
that in the most recent work Aumasson (2017), Chapter 6.
Cryptanalyze a substitution cipher in Esslinger et al. (2008).
Follow the encryption process
AES by the AES inspector in Esslinger et al. (2008).See the book Sweigart (2013a) for implementing some simpler
(symmetric) algorithms in Python, a readable
beginner-friendly programming language.
Read the parts of the book Schneier (2007) on understanding and implementing modern symmetric cryptographic algorithms.
On completion of this chapter, you will have learned about the manifold uses of (cryptographic) hash functions whose outputs serve as IDs of their input (for example, a large file).
A hash function is an algorithm that generates an
output of fixed (byte) size (usually around 16 to
64 bytes) from an input of variable (byte) size, for
example, a text or image file, a compressed archive.
hash function: algorithm that generates a fixed-size output from variable-size input
As a slogan it transforms a large amount of data into a small amount of information.
A hash function takes an input (or “message”), a variable-size string (of bytes), and returns a fixed-size string, the hash value (or, depending on its use, also (message) digest, digital fingerprint or checksum).
For example, the hash md5 (of 16 bytes) of the word
“key” in hexadecimal coding (that is, whose digits run through
0, …,9, a,b,
c,d,e and f) is
146c07ef2479cedcd54c7c2af5cf3a80.
One distinguishes between
A (simple) hash function, or checksum function, should satisfy:
That is, with respect to the second property, a hash function should behave as much as possible like a random function, while still being a fast and deterministic algorithm.
checksum function: algorithm that quickly generates a fixed-size output from variable-size input without collisions.
For example, the most naive checksum would be the sum of the bits of the input, truncated to the fixed output size. It is almost a hash function: it is fast, and it is indeed unlikely that two different messages give the same hash. However, one easily obtains two almost identical messages with the same hash. Tiny alterations could therefore go undetected.
A cryptographic (or one-way) hash function should, moreover, satisfy:
Thus the output string of fixed length that a cryptographic hash function produces from a string of any length (an important message, say) is a kind of inimitable signature. A person who knows the hash value cannot know the original message; only the person who knows the original message can prove that the “hash value” is produced from that message.
cryptographic (or one-way) hash function: a hash function such that, given an output, it is unfeasible to calculate a corresponding input.
More exactly:
weak collision resistance: computationally unfeasible to find an unknown message for a given hash.
strong collision resistance: computationally unfeasible to find two messages with the same hash.
Otherwise, an attacker could substitute an authorized message with an unauthorized one.
Hash functions are used for
querying database entries,
error detection and correction, for example,
in cryptography to identify data but conceal its content, for example,
for data authenticity checks,
for authentication, for example,
A checksum is a method of error detection in data transmission (where it also bears the name message digest) and storage. That is, a checksum detects whether the received or stored data was not accidentally or intentionally changed, that is, is free from errors or tampering. It is a hash of (a segment of) computer data that is calculated before and after transmission or storage.
That is, it is a function which, when applied to any data, generates
a relatively short number, usually between 128 and
512 bits. This number is then sent with the text to a
recipient who reapplies the function to the data and compares the result
with the original number. If they coincide, then most probably the
message has not been altered during transmission; if not, then it is
practically certain that the message was altered.
Most naively, all the bits are added up, and the sum is transmitted or stored as part of the data to be compared with the sum of the bits after transmission or storage. Another possibility is a parity bit that counts whether the number of nonzero bits, for example, in a byte, is even or odd. (The sum over all bits for the exclusive-or operation instead of the usual addition operation.) Some errors — such as reordering the bytes in the message, adding or removing zero valued bytes, and multiple errors which increase and decrease the checksum so that they cancel each other out — cannot be detected using this checksum.
The simplest such hash function that avoids these shortfalls against
accidental alterations is CRC, which will be
discussed below. It is faster than cryptographic checksums, but
does not protect against intentional modifications.
A hash table stores and sorts data by a table in which every entry is indexed by its hash (for a hash function that is fixed once and for all for the table). That is, its key is the hash of its value. This key has to be unique, and therefore the hash function ideally collision free. If not, then, given a key, first the address where several entries with this key are stored has to be looked up, and then the sought-for entry among them, causing a slow down.
Therefore, the hash size has to be chosen wisely before creating the table, just large enough to avoid hash collisions in the far future. If this can be achieved, then the hash table will always find information at the same speed, no matter how much data is put in. That is, hash tables often find information faster than other data structures, such as search trees, and frequently used; for example, for associative arrays, databases, and caches.
In practice, even for checksums, most hash functions are cryptographic. Though slower, they are still fast enough on most hardware. In fact, sometimes, for example to store passwords, they have to deliberately slow so that the passwords cannot be found quickly by their hash values through an exhaustive search among probable candidates (see rainbow tables in Section 12.6.2).
The most common cryptographic hash functions used to be
MD5, usually with an output length of 128 bit,
invented by Ron Rivest of the Massachusetts Institute of Technology in
1991. By 1996 methods were developed to create collisions for the
MD5 algorithm, that is, two messages with the same
MD5 hash. MD5CRK was a concerted effort in
2004 by Jean-Luc Cooke and his company,
CertainKey Cryptosystems, to prove the MD5
algorithm insecure by finding a collision. The project started in March
and ended in August 2004 after a collision for MD5 was found. In 2005,
further security defects were detected. In 2007 the NIST (National
Institute of Standards and Technology) opened a competition to design a
new hash function and gave it the name SHA hash functions,
that became a Federal Information Processing standard.
One exception is the Cyclic Redundance Check (CRC) which
is a fast simple hash function to detect noise, expected
accidental errors, for example, while reading a disc, such as a
DVD, or in network traffic. The CRC uses a binary
generating polynomial (a formal sum in an unknown whose only
coefficients are 0 and 1 such as
). The CRC is computed by:
1001 corresponds to
) by the generating polynomial, andThe choice of the generator polynomial is the most important one to be made when implementing the CRC algorithm; it should maximize the error-detection and minimize the chances of collision. The most important attribute of the polynomial is its length (or degree) as it determines the length of the output. Most commonly used polynomial lengths are 9 bits (CRC-8), 17 bits (CRC-16), 33 bits (CRC-32) and 65 bits (CRC-64).
In fact, the type of a CRC identifies the generating polynomial in
hexadecimal format (whose 16 digests run through
0, …, 9 and A, …,
F). A frequent CRC type is that used by Ethernet, PKZIP,
WinZip, and PNG; the polynomial
.
Again, the CRC can only be relied on to confirm the integrity against accidental modification; through intentional modification, an attacker can cause changes in the data that remain undetected by a CRC. To prevent against this, cryptographic hash functions could be used to verify data integrity.
SHA stands for Secure Hash Algorithm. The
SHA hash functions are cryptographic hash functions made by
the National Security Agency (NSA) and the National Institute of
Standards and Technology. SHA-1 is the successor to
MD5 with a hash size of 160 bits, an earlier,
widely-used hash function, that fell victim to more and more suspicious
security shortcomings (even though it is not downright broken; for
example, there is no known computationally feasible way to produce an
input for a given hash ). SHA-1 was notably used in the Digital
Signature Algorithm (DSA) as prescribed by the Digital Signature
Standard (DSS) by the Internet Engineering Task Force.
In the meanwhile, there are three SHA algorithms SHA-1,
SHA-2 and SHA-3, released in 2015 of
ever-increasing security, mitigating the shortcomings of each
predecessor. “SHA-2” permits hashes of different bit sizes; to indicate
the number of bits, it is appended to the prefix “SHA”, for example,
“SHA-224”, “SHA-256”, “SHA-384”, and “SHA-512”.
A hash function should be
So if, for example, the output has 256 bits, then
ideally each value should have the same probability
.
That is, the output identifies the input practically uniquely
(with a collision chance of ideally
);
So one might think of a data hash, for example, from a file, as its
ID card (or more accurately, identity number); a hash
identifies much data by little information.
Since the length of the hash sequence is limited (rarely bits), while the length of the input sequence is unlimited, there are collisions, that is equal hashes from different files. However, the algorithm minimizes the probability of collisions by distributing their values as evenly as possible: Intuitively, make them as random as possible; more accurately, every possible fixed-length sequence is a value and the probability of each of the values is the same.
It is cryptographic (or one-way)
Cryptographic or One-Way hash function: a hash function such that it is computationally infeasible to find an input for a given output and similar inputs have dissimilar output.
More exactly, the algorithm should resist
According to Kerckhoff’s principle, the algorithm should also be public. In practice,
MD4, MD5 and
SHA-1 that do not resist against collisions attacks, but
are still in use.For example, the CRC algorithm is a hash function (not
cryptographic); Common cryptographic hash functions are, for example,
MD4, MD5, SHA-1,
SHA-256 and SHA-3.
For example, the output of the hash function SHA-256 of
ongel is
bcaec91f56ef60299f60fbce80be31c49bdb36bc500525b8690cc68a6fb4b7f6.
The output of a hash function, called hash, but also
message digest or digital fingerprint, depending on
the input, is used, for example, for message integrity and
authentication.
The most commonly used hash (cryptographic) algorithms even today are
16 bytes (=128 bits) MD4 and
MD5 or SHA-1, which uses 20 bytes
(= 160 bits). Although all of these, MD4,
MD5 and SHA-1 do not withstand collision
attacks, they remain popular for use. Their implementation details are
described in RFCs (Request for Comments): an
RFC publicly specifies in a text file the details of a
proposed Internet standard or of a new version of an existing standard
and are commonly drafted by university and corporate researchers to get
feedback from others. An RFC is discussed on the Internet and in formal
meetings of the working group tasked by the Internet Engineering Task
Force (IETF). For example, networking standards such as IP and Ethernet
have been documented in RFCs.
MD4 (Message-Digest algorithm):
RSA algorithm (and the RSA Data Security
company);RFC 1320 .MD5:
Developed by RSA Data Security.
Described in RFC 132.
Vulnerable to collisions, but not to creating a second reverse image. Often used for
P2P, or Peer-to-Peer, in English), andSHA-1 (Secure Hash Algorithm):
instead of MD4, MD5 or the ancient
SHA-1, recommended are more recent versions like
SHA-256 and SHA-3 of the
Secure Hash Algorithm.
Secure Hash Algorithm: Hash algorithm recommended by the National Institute for Standards and Technology.
Similar to modern symmetric ciphers that follow the design laid out by Feistel’s Lucifer algorithm in the 70s, cryptographic hash functions follow the Merkle-Damgård construction:
The Merkle meta-method, or the Merkle-Damgård construction, builds from a lossless compression function (that is, whose inputs have the same length as the output) a lossy compression function, that is, a hash function. This method allows us to reduce the immunity of the entire hash function against
to the corresponding immunity of the compression function.
This construction needs
IV = initialization
value),C, andWith , one computes for That is, for the computation of the hash of the current block, the value of the compression function of the last block enters jointly with the current block value.
The C compression function consists of a Feistel Cipher
(or substitution and permutation network)
where
XOR ) to
. This is
XOR ) to
. This is
The addition of
ensures that the C compression function is no longer
invertible (unlike the
cipher for a fixed key); that is, for a given output, it is no longer
possible to know the (unique) input. Otherwise, to create a collision,
given an output
, one could decipher by different keys,
and
to get different entries
and
.
To reduce the immunity from hash to compression function, the padding needs to meet sufficient conditions:
The simplest pad that meets these conditions is the one that attaches
the length
to
and fills the segment between the end of
and
by the number of 0 s prescribed by the block size, that is,
the concatenation
Observation: To avoid collisions, it is not enough for the padding to fill with zeros the rest of the message: This way, two messages that only differ in the number of final zeros at the last end would have the same padding!
Instead, the simplest way would be to attach a digit 1,
and then the rest with 0s. However, we will see that this
would allow collisions with the Merkle meta-method if the initial value
IV was chosen in the following way:
Denote
the message blocks and IV the starting value. The hash is
calculated by iterating the compression function
The clou of Merkle’s meta-method is the
reduction of collisions from the hash function to the compression
function: a hash collision would imply a collision of the compression
function, that is, different pairs of
and
blocks with
.
To see this, we note that
Without the length in the padding, the collision of two messages with
different lengths can ultimately only be reduced to a pre-image of the
initial value IV under the compression function, that is, a
value B such that
If its choice were arbitrary, the authors of MD5 and
SHA-256 could however have inserted the following back
door: Both algorithms use Mayer-Davis’s scheme, that is, a compression
function
for a Feistel cipher E
with a key
; in particular, with
fixed the decryption function
is invertible! Now, if the authors wanted to, they could have chosen a
key
and set
exactly so that
IV = C(IV,K). Then C(IV, B) = C(C(IV, K), B) ,
that is, a collision between the hashes of
and
!
Since, for example, MD5 and SHA-256 choose
as IV a value whose pre-image is supposedly not known (for
example, the hexadecimal digits in ascending order in MD5
or the decimal digits of the first eight primes in SHA-256)
this problem is more theoretical than practical.
We won’t study the inner workings of SHA-256 in detail
(in contrast to O’Connor (2022)), but a schematic look at its
design shows that it follows the Merkle-Damgård construction:
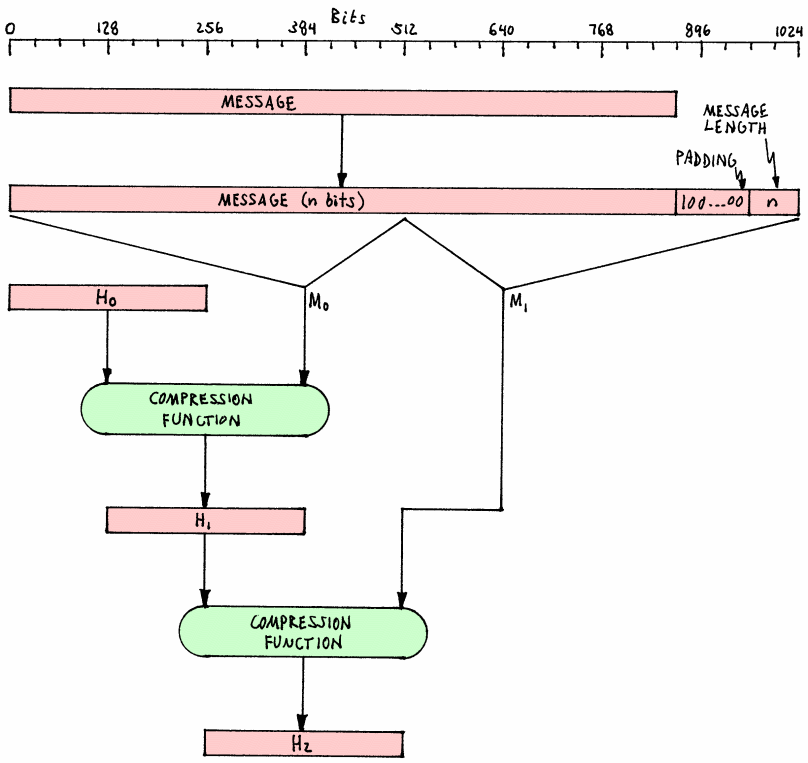
It is then iterated in roughly 64 rounds:
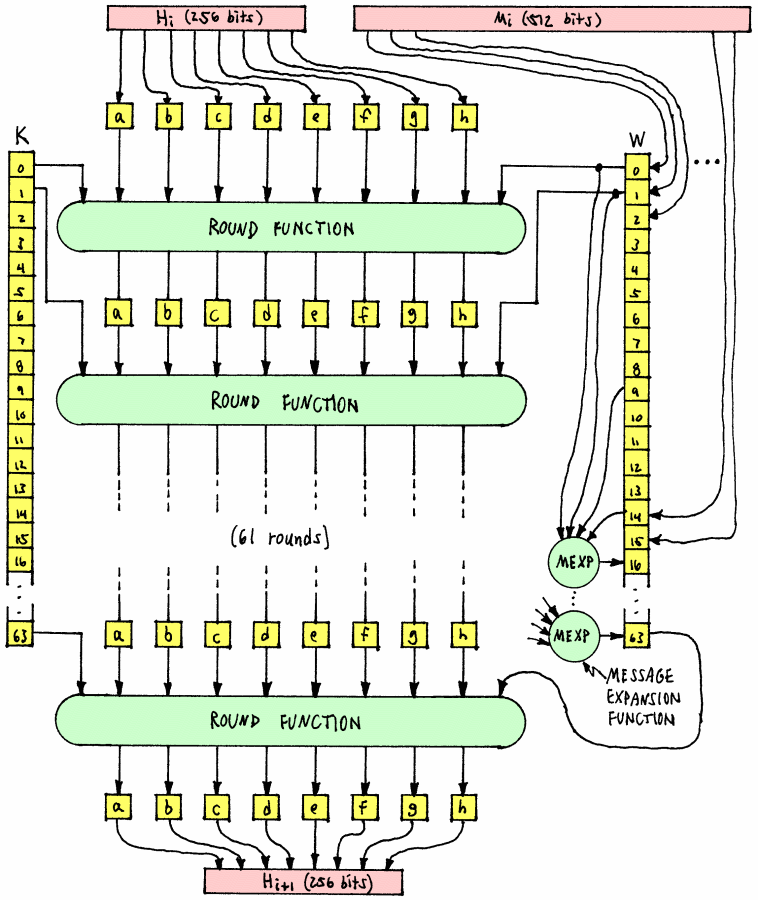
On Lynn-Miller (2007), you can trace the bytes of an
input of your choosing at each step of the SHA-1
algorithm.
Uses of cryptographic hash functions abound:
If the roles of the public and private key are flipped, then the
encryption is a digital signature: while the encrypted
message will no longer be secret, every owner of the public key can
check whether the original message was encrypted by the private key.
However, in theory, signing a file (using the RSA
algorithm) that was encrypted using the RSA algorithm would
decrypt it. Therefore, in practice, since for a signature it suffices to
unequivocally identify the signed file (but its content often secret,
for example, when signing a secret key), usually a cryptographic
hash is encrypted by the private key.
A message authentication code algorithm uses a one-way hash function (such as MD5 or SHA-1) and a block cipher that accepts a secret key and a message as input to produce a MAC. The MAC value provides the intended receivers (who know the secret key) to detect any changes to the message content by:
Hash functions (not necessarily cryptographic, like
CRC) are used:
for fast data query (that is, at fixed time, regardless of the number of entries, for example,
to ensure the integrity of a file in case of accidental modifications, that is, to detect differences between the file and a reference version (typically the one before the file is transported).
Cryptographic Hash functions are used:
key stretching),
intuitively make them less predictable; that is, as KDF (=
Key Derivation Function);
PBKDF (=
Password Based Key Derivation Function).Observation: Note the difference between authenticity and authentication: The former guarantees the equality of data received and sent from a person (for example, in the digital signature), the latter the identity of that person (for example, in a secure site access).
The cryptographic hash algorithms listed above, MD4/5,
SHA … distribute the values evenly, but are fast;
so they are unsuitable for password creation because they are vulnerable
to brute-force attacks. To prevent these, the PBKDF
algorithm, for example, PBKDF1, PBKDF2,
bcrypt, scrypt, Argon2 (a new and
more promising candidate), are
bcrypt,scrypt algorithm;salt, an
additional, unique, usually random argument. Without salt,
the algorithm is prone to attacks by so-called
Rainbow Tables, tables of the hashes of the most common
passwords.A h table (or scatter table) uses a hash function to address the entries (= rows) of a array, that is, a data table.
Each entry has a name, that is, a unique identification (= key). For example, the key is the name of a person. The key data, for example, your telephone number, is stored in a table row. These rows are numbered from .

The row number, your address, of the key is determined by your hash. As an advantage, at a fixed time, the data can
While,
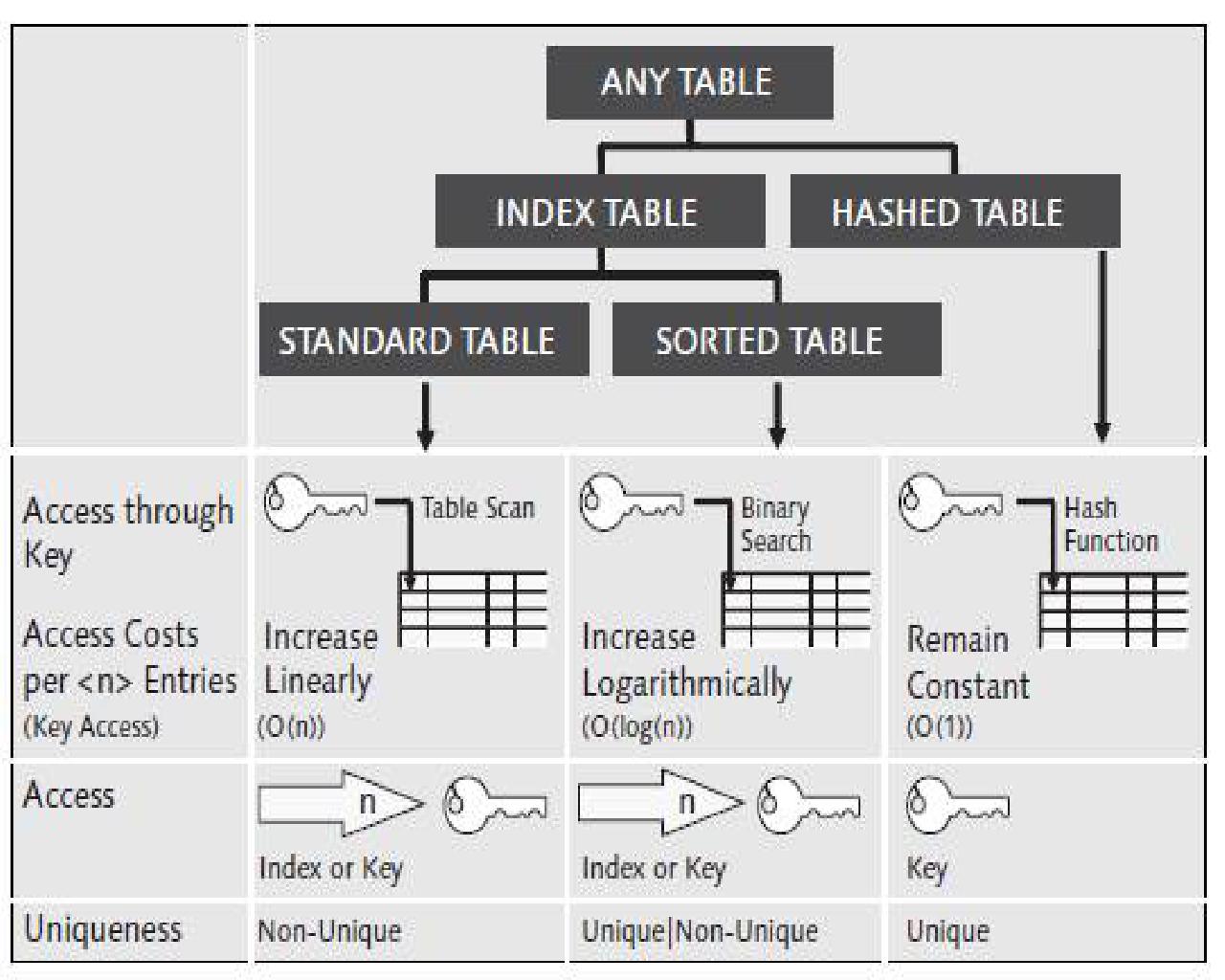
Collisions, that is, two entrances with the same hash are more frequent than you might think; see the Birthday Paradox. To avoid collisions, it is necessary
When collisions occur, a strategy is
instead of the hash number address a single entry, use
Chaining: address a bucket, a bucket of
multiple entries, a list, or
use “Open Hashing. put the entry in another free position, for example,
Double Hashing).Up to of the table being filled, on average collisions occur. That is, finding an entry takes operations. To compare, with entries, it would take on average
However, after this factor collisions occur so often that the use of another data structure, for example a binary tree, is recommended.
A spreading or Merkle tree
(invented in 1979 by Ralph Merkle) groups data into blocks
by a tree (binary), whose vertices (= nodes) are hashes and
whose sheets (= end nodes) contain the data blocks, in order to
be able to quickly check (in linear time) each data block by
computing the root hash.
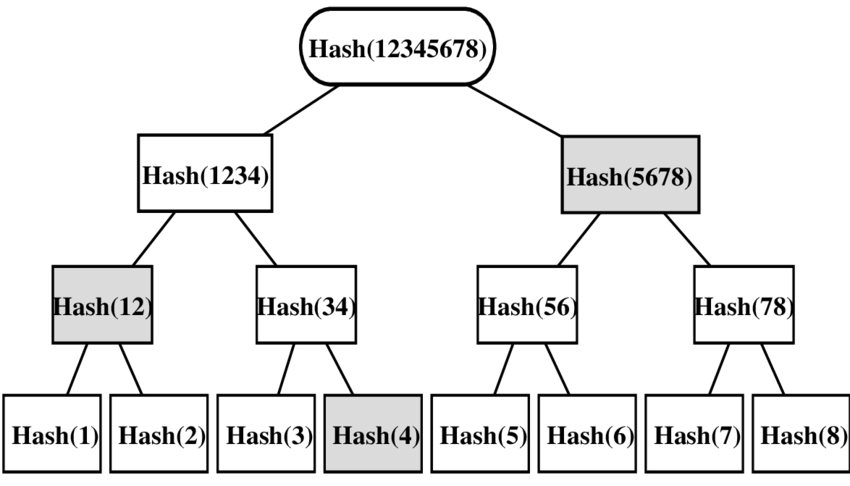
In a (= sheets )deep scattering tree the data block of each sheet is verifiable
The main use of Merkle trees is to ensure that blocks of data received from other pairs in a point-to-point network (P2P) are received intact and unchanged.
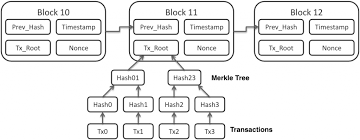
A Merkle tree is a (usually binary) hashes tree whose
leaves are data blocks from a file (or set of files). Each node above
the leaves on the tree is the hash of its two children. For example, in
the image,
Hash(34) is the hash of the concatenation of the hashes
Hash(3) and Hash(4), that is,
,Hash(1234) is the hash of the concatenation of the
hashes Hash(12) and Hash(34), that is,
,
andHash(12345678) is the hash of the
concatenation of the hashes Hash(1234) and
Hash(5678), that is,
.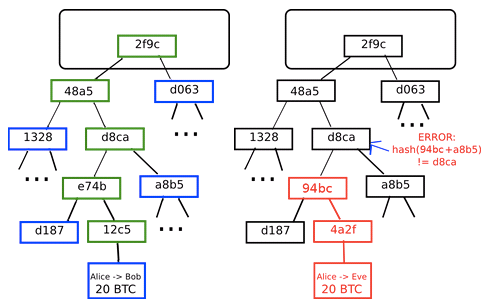
Normally a
cryptographic shuffling function' is used, for example,SHA-1. However, if the Merkle tree only needs to protect against unintentional damage, "checkums" are not necessarily cryptographic, such asCRC`s
are used.
At the top of the Merkle tree resides the root-dispersion or
master-dispersion. For example, on a P2P network,
root dispersion is received from a trusted source, e.g. from a
recognized website. The Merkle tree itself is received from any point on
the P2P network (not particularly reliable). This (not
particularly reliable) Merkle tree is compared by calculating the leaf
hashes with the reliable root dispersion to check the integrity of the
Merkle tree.
The main advantage of a tree (deep
with
leaves, that is, blocks of data), rather than a dispersion
list, is that the integrity of each leaf can be verified by calculating
(rather than
)
hashes (and its comparison with the root hash).
For example, in Figure 3.1, the integrity check requires only
Hash(4)
Hash(12), and Hash(5678), andHash(3)
Hash(34), Hash(1234), and
Hash(12345678)Hash(12345678)
and the hash obtained from the trusted source.A hash function transforms any data (such as a file), in
other words, a variable-length string, into a
fixed-length string (which is usually 16 or
32 bytes long); as a slogan, it transforms a large amount
of data into a small amount of information. Their
output, a hash, can be thought of as an ID-card of their input
(such as a file); to this end, the hash function should
So if, for example, the output has 256 bits, then
ideally each value should have the same probability
.
That is, the output identifies the input practically uniquely
(with a collision chance of ideally
);
It is cryptographic (or one-way)
Recommended are, among others, the more recent versions
SHA-256 and SHA-3 of the
Secure Hash Algorithm.
How do a checksum and cryptographic hash function differ? Only for a cryptographic hash function it is unfeasible to create collisions.
What are typical uses for checksums? (Accidental) error detection and correction, for example, noise on reading a Compact Disc or in network traffic, and many more.
What are typical uses of cryptographic hash functions? (Intentional) alteration correction in storage or network traffic, and many more.
Name common cryptographic hash functions. The MD and the SHA family.
Which hash function is not cryptographic ? SHA-1, MD4, CRC, WHIRLPOOL
Which cipher is a stream cipher? RSA, Enigma, AES, DES
Read the section on symmetric cryptography in the article Simmons et al. (2016).
Read (at least the beginnings of) Chapter 9 on hash
functions in Menezes, Oorschot, and Vanstone (1997), and (at least the beginnings of)
that in the most recent work Aumasson (2017), Chapter 6.
Observe the diffusion created by a cryptographic hash function in Lynn-Miller (2007).
On completion of this chapter, you will have learned …
The big practical problem of single-key cryptography is key distribution, more exactly:
In 1976, Whitfield Diffie and Martin Hellman conceived that the key distribution problem could be solved by an algorithm that satisfied:
(computationally) easy creation of a matched pair of keys for encryption and decryption,
(computationally) easy encryption and decryption,
(computationally) infeasible recovery of one of the keys despite knowledge of:
(computationally) infeasible recovery of the plaintext for almost all keys and messages .
Observation: This was the first public appearance of two-key cryptography. However, the British Government Communications Headquarters (GCHQ) knew it around a decade earlier.
If a user, say Alice, of such an algorithm keeps her decryption key secret but makes her encryption key public, for example, in a public directory, then:
The security of two-key cryptographic algorithms relies on the computational difficulty of a mathematical problem, for example, factoring a number that is the product of two large primes; ideally, computing the secret key is equivalent to solving the hard problem, so that the algorithm is at least as secure as the underlying mathematical problem is difficult. This has not been proved for any of the standard algorithms, although it is believed to hold for each of them.
In comparison with symmetric cryptography, asymmetric encryption avoids the risk of compromising the key to decipher that is involved in exchanging the key with the cipherer. This secure communication with anyone via an insecure channel is a great advantage compared to symmetric cryptography. Let us recall the classic methods to exchange a symmetric key, before looking at its asymmetric counterpart: While asymmetric cryptography made it possible to exchange a secret key overtly, this convenience comes at the risk of the unknown identity of the key holder, prone to a man-in-the-middle attack which Public Key Infrastructure work around by the use of certificates, digital signatures by third parties of public keys.
A symmetric key must be passed secretly. Possible methods are:
Derivation from a base key using a Key Derivation Function (KDF), a cryptographic hash function which derives a secret key from secret — and possibly other public — information, for instance, a unique number,
Creating a key from key parts held by different persons, for example, as an analogue to the one-time pad: If is the secret (binary number, then for the partial secrets , , … Reconstruction of is only possible if all , , … are combined
transmission via a different channel, for example:
Diffie and Hellman’s achievement was to separate secrecy from authentication: Ciphertexts created with the secret key can be deciphered by everyone who uses the corresponding public key; but the secret-key holder has no information about the owner of the public key!
Thus the public keys in the directory must be authenticated.
Otherwise A could be tricked into communicating with
C when he thinks he is communicating with B by
substituting C key for B in A’s
copy of the directory; the man-in-the-middle attack
(MIM):
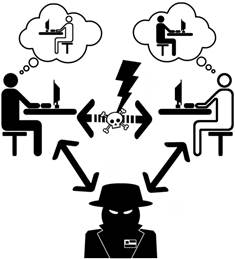
Man-in-the-middle attack: an attacker intercepts the messages between the correspondents and assumes towards each of them either correspondent’s identity.
In an MITM, the attacker places himself between the
correspondents, assuming towards each one of them the identity of the
other to intercept their messages.
So both Alice and Bob are convinced to use each other’s public key, but they are actually Eve’s!
In practical terms, this problem occurs for example in the 1982 ‘ARP’
Address Resolution Protocol (in RFC 826) which standardizes the address
resolution (conversion) of the Internet layer into link layer addresses.
That is, ARP maps a network address (for example, an
IPv4 address) to a physical address as an
Ethernet address (or MAC address). (On
Internet Protocol Version 6 (IPv6) networks, ARP has been replaced by
NDP, the Neighbor Discovery Protocol).
The ARP poisoning attack proceeds as follows:
Maria Bonita wants to intercept Alice’s messages to Bob, all three being part of the same physical network.
Maria Bonita sends a arp who-has packet to Alice which
contains as the source IP address that of Bob whose identity we want to
usurp (ARP spoofing) and the physical MAC
address of Maria Bonita’s network card.
MAC
address of Maria Bonita with Bob’s IP address.IP level, it
will be Maria Bonita who will receive Alice’s packages!Let us recall that there are two keys, a public key and a private key. Usually:
Thus, a text can be transferred from the encipherer (Alice) to one person only, the decipherer (Bob).
The roles of the public and private keys can be reversed:
Thus, the encipherer can prove to all decipherers (those who have the public key) their ownership of the private key; the digital signature.
The (mathematical) algorithm behind the encryption either by the
public key (for hiding the content of digital messages) or by the
private key (for adding digital signatures) is in theory almost the
same: only the roles of the arguments of the one-way function are
exchanged (for example, in the RSA algorithm). In practice,
however, usually:
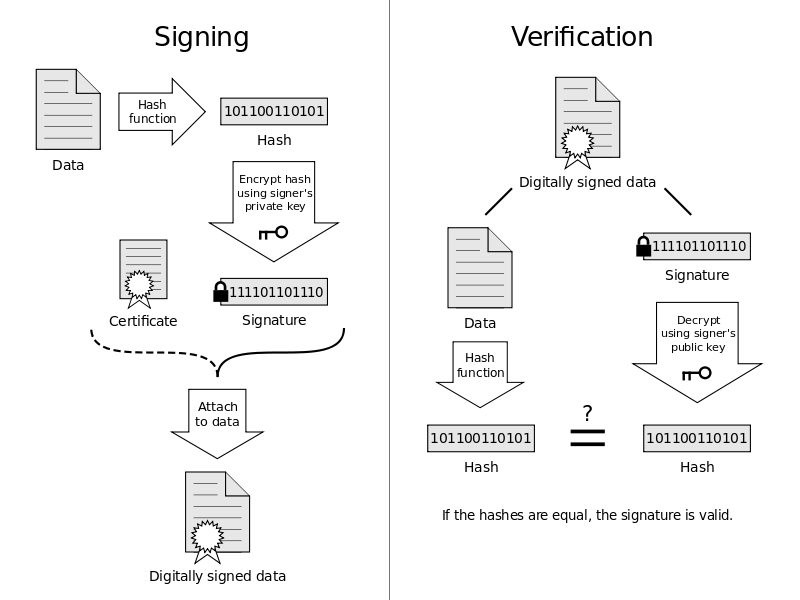
That is, while
A sub-key of a master key is a key (whose cryptographic checksum is) signed by the master key. The owner often creates subkeys in order to use the main key (public and private) only
to sign
to revoke a key (that is, sign a revocation),
to change the expiration date of a personal key.
The subkeys are used for all other daily purposes (signing and deciphering).
This way, if a sub key is eventually compromised (which is more likely that that of a main key due to its everyday use), then the main key will not be compromised. In this case,
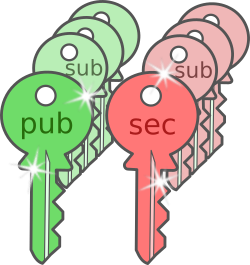
We saw how subkeys work in practice in the common
command-line program GPG discussed in Section 13.4. A good reference is https://wiki.debian.org/Subkeys.
For more security, you create (for example, in GPG)
first a (public and private) main key and
then several sub keys with expiry date, for everyday use:
Before their expiry, the keys are either extended, or revoked to create others.

As for using different keys to sign and encrypt,
it’s necessary for some algorithms, for example,
it is safer (but more inconvenient, which can lead to the user’s sloppiness and then in practice it is less safe!) to have different keys to decipher and to sign,
because
because, for example in the RSA algorithm, the
signature and the decipherment (by the private key) are equal (in
theory, though in practice implemented differently) algorithms!
Therefore, signing (by the private key) a document encrypted by the
corresponding public key is equivalent to deciphering it! However, this
possibility is theoretical, but it does not practice: All
implementations of the RSA protect the user by the fact
that always and exclusively
Only the main key is immutably linked to the identity of the owner, and all others replaceable: While the
main key is kept in a safe at home and only sees the light when keys need to be signed (be it from the owner or from someone else [for example, to establish the web of trust]).
In practice,
is stored on a flash drive or memory card,
and to be more durable, it is even printed, for example:
By the paperkey program that extracts the secret
part (of the file) of the private key (that is, it omits all public
information like
and encodes this part in hexadecimal notation (stored in a text
file). (So if the key has, for example,
bits, the file generated by paperkey has
bits). This command
gpg --export-secret-key 0xAE46173C6C25A1A1! > ~/private.sec
paperkey --secret-key ~/private.sec > ~/private.paperkey!) the main secret key
(0xAE46173C6C25A1A1) of the private keys, andpaperkey into a text
file.By the qrencoder program (for keys whose file has
characters) which encodes it into a QR code.
the sub keys are stored in a smartcard that is accessed by a USB reader with its own keyboard. Compared to using a digital file, it has the advantage that
reading the keys on a smart card is much more difficult than a file (stored on a USB stick or hard drive)
leaves fewer traces:

(Perfect) Forward Secrecy means that, after the
correspondents exchanged their (permanent) public keys and established
mutual trust,
MITM attack (see Section 4.2),This way, even if the correspondence was eavesdropped and recorded, it cannot be deciphered later; in particular, it cannot be deciphered by obtaining a correspondent’s private key.
For example, the TLS protocol, which encrypts
communication of much of the Internet, has since version 1.2 support for
Perfect Forward Secrecy: In the handshake between client and server in
Section 13.3 : after the client has received (and
trusted) the server certificate, the server and the client exchange a
ephemeral public key which serves to encrypt the communication
of only this correspondence. This ephemeral key is signed by the public
(permanent) key of the server. (The creation of this asymmetric key in
Perfect Forward Secrecy makes the creation of a symmetric
preliminary key by the client in the penultimate step in the
handshake in the TLS protocol superfluous.)
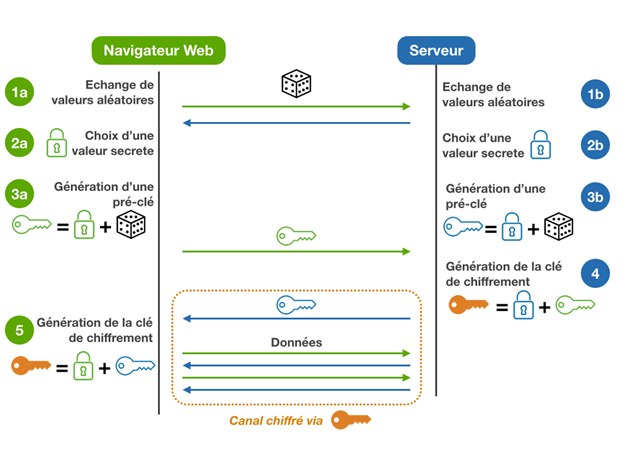
Every granted signature shall first be thought through solemnly. The same goes for digital signatures:
A signature proves that the owner of the private key, say Alice, acknowledged the content. In e-mail communication, it avoids the risk that an attacker
However, if the communication contains something Alice doesn’t want to be seen by others (for example, to be read out loud by a prosecutor in court), better not prove her acknowledgement! Since this message may eavesdropped, her correspondent may change his mind about the privacy of their conversation, or his account is hacked, …
To give an analogy to our analog reality, an automatic digital signature by Alice compares to the recording of every private conversation of Alice.
In fact, usually Alice wants to prove only to Bob that she’s the sender, but not to third parties! For this, in a group signature, an ephemeral key to sign is created and shared (that is, the public and private key) between Alice and Bob. This way, Alice and Bob are sure that the message was sent by the other correspondent, but a third party only that it was sent among the group members.
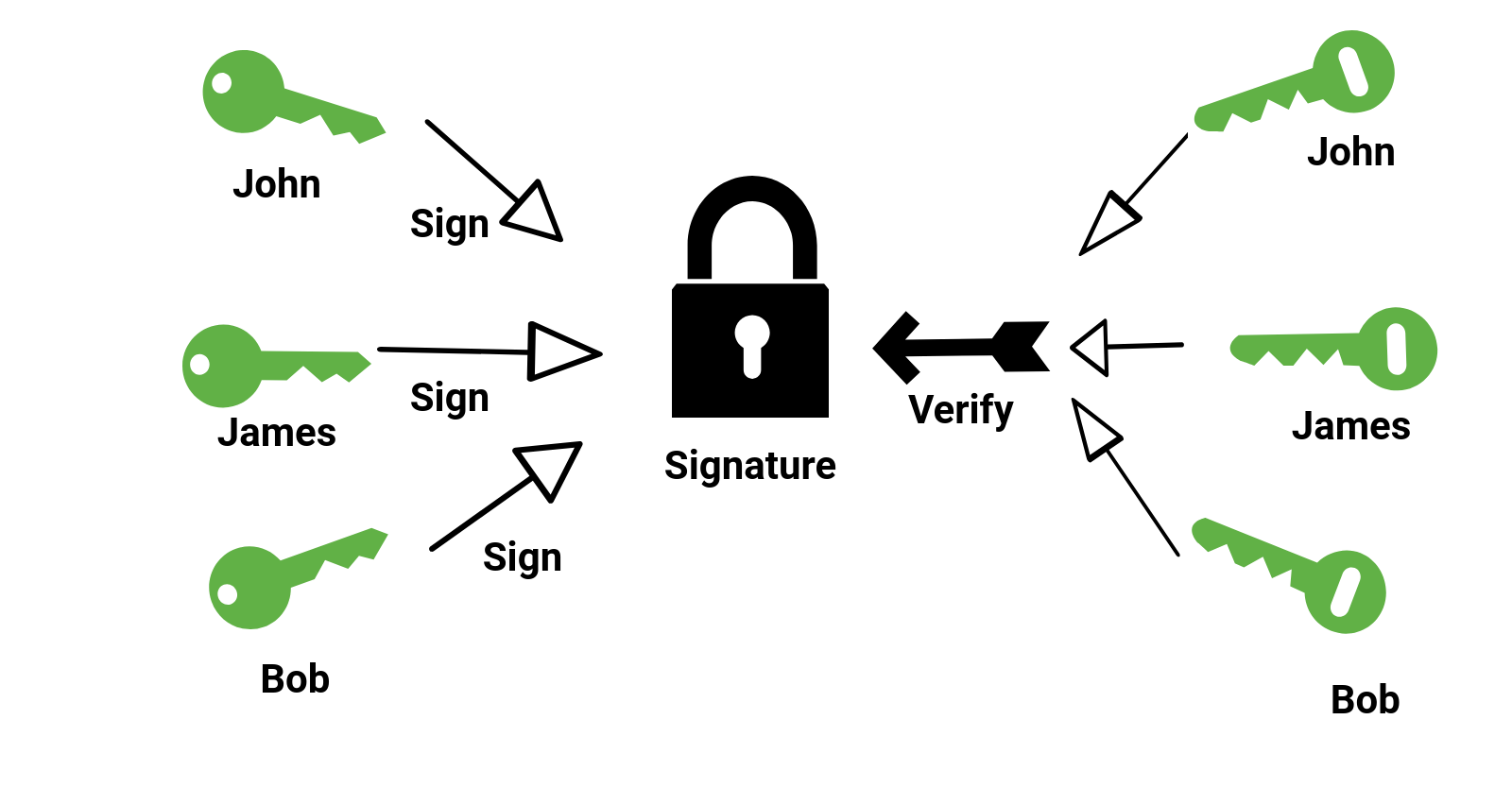
A Public Key Infrastructure (PKI) of a network establishes trust among its spatially separated users by first authenticating them, then authorizing their public keys by signing them (referred to as digital certificates) and finally distributing them. In institutions and corporations, a PKI is often implemented as “a trust hierarchy” of Certification Authorities, whereas in looser communities it can be decentralized and trust mutually established by the users themselves.
A Public Key Infrastructure (PKI): establishes trust among its spatially separated users of a network by first authenticating them, then authorizing their public keys by signing them (referred to as digital certificates) and finally distributing them.
A PKI includes:
(Digital) Certificates: public keys which are signed to authenticate their users. Other then the name and key, they contain additional personal data, such as an e-mail address, and usually an expiry date.
Certificate Revocation List (CRL): A list of certificates that have been revoked before their validity expires, for example, because
Directory Service: a searchable database of the emitted certificates; for example, in a trust hierarchy an LDAP server (Lightweight Directory Access Protocol; a standard used by large companies to administer access of users to files, printers, servers, and application data), and in the web of trust a server that hosts a database searchable by a web form.
The identity of the key owner is confirmed by third parties, that is, other identities with private keys that confirm by their digital signatures that it is Alice who owns the private key.
However, the problem of the public key identity arises again: How can we ensure the identities of the private key owners? There are two solutions:
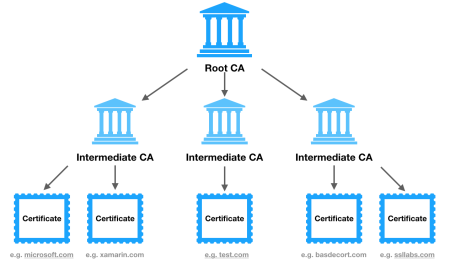
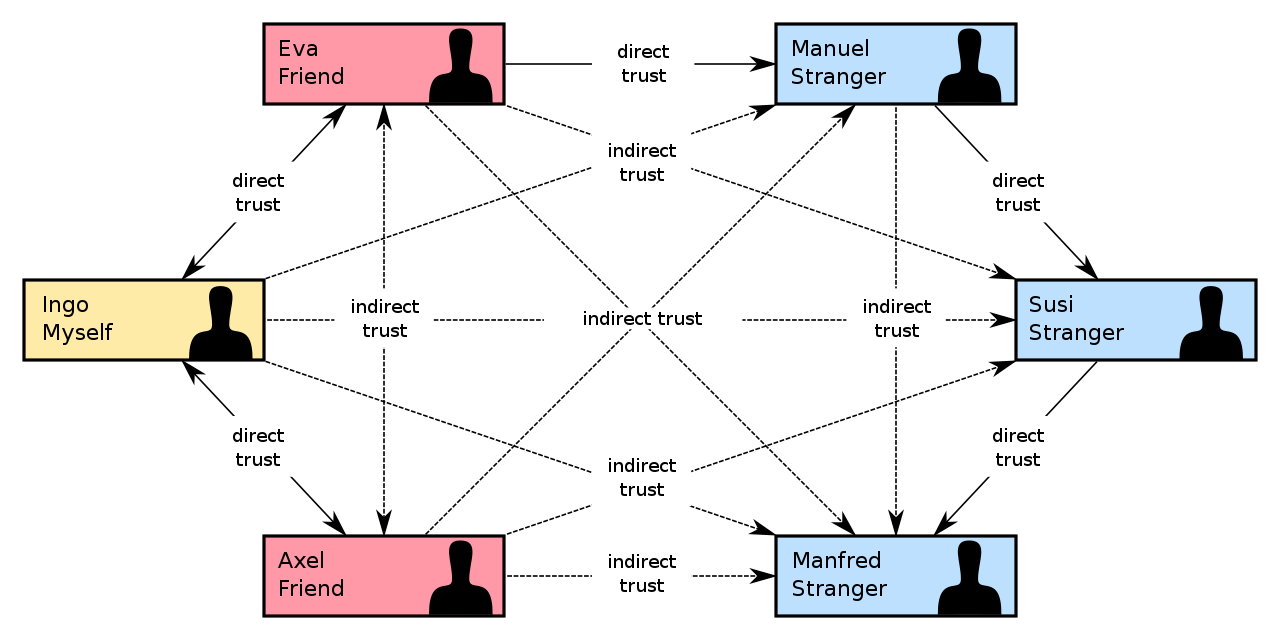
For short: while in the Web-of-Trust the connections built by trust form a graph, in the approach by hierarchical authorities they form a tree.
In the approach via hierarchical authorities, private key owners are distinguished by hierarchical levels. At the highest level lie the root authorities on which one trusts unconditionally.
hierarchical authorities: Key owners that confirm others’ identities by digital signatures and are organized in a hierarchy, where trust passes from a higher to a lower level; total trust is placed in those at the highest level, the root authorities.
For example,
VeriSign, GeoTrust, Commode, … are major US certifying companies;
as a recent addition, the (US intermediary) non-profit authority
Let us encrypt;
a look at the /etc/ssl/certs folder in the Linux
distribution openSUSE reveals that there is, for
example,
TeleSec of
Deutsche Telekom AG, the former national telecommunications
operator), Firmaprofesional, ACCVRAIZ1
— Agencia de Tecnología y Certificación Electrónica, and
ACC RAIZ FNMT — Fábrica Nacional de Moneda y Timbre),
andIn the web of trust, private key owners cannot be distinguished from each other.
web of trust: Private key owners confirm other’s identities by successively passing trust to each other among equals.
The absence of root authorities, unconditionally trusted entities, is compensated for by the
trust initially established by
having obtained the public key personally (for example, at key-sign parties, meetings where participants exchange and sign their public keys mutually), or
by
SMS, instant messenger, …);then the trust is successively (transitively) passed from one to the other: If Alice trusts Bob, and Bob trusts Charles, then Alice trusts Charles.
On the Internet,
X.509, principally used
to encrypt the communication between a user and a (commercial) Website
(but also between users in corporate environments, such as,
S/MIME e-mail encryption), andOpenPGP scheme (as implemented by the
GnuPG program), with its main use of encrypting e-mails.
This scheme radically rejects any hierarchy: the user can publish a
public key with an e-mail address on a public key server such as that of
the MIT without even confirming (by an activation e-mail) that he has
access to the account of this e-mail address.The IETF (Internet Engineering Task Force) proposed (in RFC 63941: DANE use cases and RFC 66982: DANE protocol) the DANE protocol that aims to cryptographically harden the TLS, DTLS, SMTP, and S/MIME protocols using DNSSEC. By DNSsec, a DNS resolver can authenticate a DNS resolution, that is, whether it is identical to that on the authoritative DNS server, by checking its signature (of the authoritative DNS server). Instead of relying, like these protocols, entirely on certificate authorities (CAs), domain holders
Using CAs, there is no restriction on which CAs can issue certificates for which domains. If an attacker can gain control of a single CA among the many CAs that the client trusts, then she can emit fake certificates for every domain. DANE allows clients to ask the DNS servers, which certificate are trustworthy so that the domain holder can restrict the scope of a CA. When the user is passed a domain name certificate (as part of the initial TLS handshake), the client can check the certificate against a TLSA resource-record (TLSA-RR) published in the DNS for the service name which is authenticated by the authoritative DNS server.
The most common standard for a PKI is the hierarchy of
X.509 certificate authorities. X.509 was first published in
1998 and is defined by the International Telecommunications Union’s
Standardization sector (ITU-T), X.509 establishes in particular a
standard format of electronic certificate and an algorithm for the
validation of certification path. The IETF developed the most important
profile, PKIX Certificate and CRL Profile, or “PKIX” for short, as part
of RFC 3280, currently RFC 5280. It is supported by all common web
browsers, such as Chrome and Firefox, which come with a list of
trustworthy X.509 certificate authorities.
In more detail, the TLSA-RR contains the entry Certificate Usage,
whose value (from 0 to 3, the lower, the more
restrictive) restricts the authority allowed to validate the certificate
for the user:
The DANE check therefore serves to confirm certificates issued by public certification authorities. With DANE values (2 and 3), the domain holder has the option of creating his own, even self-signed certificates for his TLS-secured services, without having to involve a certification authority known to the client. By choosing between “Trust Anchor” (TA) and “End Entity” (EE), the domain owner can decide for himself whether to anchor DANE security to a CA or server certificate.
hybrid encryption: a two-key algorithm is used to authenticate the correspondents by digitally signing the messages or to exchange a key for single-key cryptography for efficient communication thereafter,
The most common key exchange method is to create a shared secret between the two parties by the Diffie-Hellman protocol and then hash it to create the encryption key. To avoid a man-in-the-middle attack, the exchange is authenticated by a certificate, that is, by signing the messages with a long term private key to which the other party holds a public key to verify. Since single-key cryptographic algorithms are more efficient than two-key cryptographic algorithms by a considerable factor, the main use of two-key encryption is thus so-called hybrid encryption where the two-key algorithm is used
For example, in the TLS (Transport Layer Security;
former SSL) protocol, which encrypts secure sites on the World Wide Web,
a cryptographic package such as
TLS_RSA_WITH_3DES_EDE_CBC_SHA (identification code
0x00 0x0a) uses
RSA to authenticate and exchange the keys,3DES in CBC mode to encrypt the
connection, andSHA as a cryptographic hash.X.509 (as used by S/MIME) and
OpenPGPSingle-key (or symmetric) cryptography suffers from the key distribution problem: to pass the same secret key to all, often distant, correspondents. Two-key (or asymmetric) cryptography solves this problem seemingly at once, by enabling the use of different keys to encrypt and decrypt. However, the identity of the key owner must be confirmed; if not personally, then by third parties, that is, identities with private keys that confirm by their digital signatures that it is Alice who owns the private key. However, the problem of the public key identity arises again: How can we ensure the identities of these private key owners? There are two solutions: In the approach via hierarchical authorities, private key owners are distinguished by hierarchical levels. At the highest level lie the root authorities on which one trusts unconditionally. In the web of trust, trust is transferred from one to the other, that is, trust is transitive: If Alice trusts Bob, and Bob trusts Charles, then Alice trusts Charles.
Read the section on asymmetric cryptography in the article Simmons et al. (2016). Read in Menezes, Oorschot, and Vanstone (1997) Sections 3.1 and 3.3.
Read the parts of the book Schneier (2007) on understanding and implementing modern asymmetric cryptographic algorithms.
On completion of this chapter, you will have learned what a trapdoor function is, and:
The security of two-key cryptographic algorithms relies on the computational difficulty of a mathematical problem, for example, factoring a number that is the product of two large primes; ideally, computing the secret key is equivalent to solving the hard problem, so that the algorithm is at least as secure as the underlying mathematical problem is difficult. This has not been proved for any of the standard algorithms, although it is believed to hold for each of them.
To see the usefulness of (modular) arithmetic in cryptography, recall that asymmetric cryptography is based on a trapdoor function, which
The ease of calculating the function corresponds to the ease of
encryption, while the difficulty of calculating the inverse corresponds
to the difficulty of decryption, that is, inverting the encryption. For
example, RSA uses
While both, the function itself and even its inverse, are easily
computed using the usual multiplication of numbers, instead
cryptographic algorithms (such as RSA) use modular
arithmetic to entangle the computation of the inverse function
without knowledge of the key (which in RSA is root
extraction).
We already know modular or circular arithmetic from the arithmetic of the clock, where is considered equal to : Because the indicator restarts counting from after each turn, for example, hours after hours is o’clock: Over these finite circular domains, called finite rings and defined in Section 5.3, (the graphs of) these functions become irregular and practically incomputable, at least without knowledge of a shortcut, the key.
In what follows, we
The difficulty of calculating the inverse corresponds to the difficulty of decryption, that is, inverting the encryption. In an asymmetric cryptographic algorithm,
are based on an invertible function such that
For example, the inverses of the trap-door functions
RSA algorithm), andDiffie-Hellman algorithm)are given by
They are
Observation. Both functions are algebraic, that is, they are expressed by a formula of sums, products, and powers. Analytical functions, that is, infinite convergent sums, for example, sine, cosine, …, are inconvenient by the rounding errors.
The domain of these functions is not the set of integers (or that of the real numbers that includes them), because both functions, exponentiation and raising to a power, are continuous over :
If the domain of these functions were , then their inverses could be approximated over , for example, by iterated bisection where the inverse point is besieged in intervals that are halved at every iteration: Given , find an such that is equivalent to finding a zero of the function
(Start) Choose an interval such that
(Recalibration) Calculate the midpoint of the interval :
Otherwise:
and recalibrate the newly obtained interval respectively .
By the Intermediate Value Theorem, the zero is guaranteed to be in the interval, which at each step decreases and converges to the intersection.
Finding the zero of the polynomial by bisection with starting points and , yields in steps the successive approximations
To avoid the iterative approximation of the zero of a function and thus complicate the computation of the inverse function (besides facilitating the computation of the proper function), the domain of a trapdoor function is a finite ring denoted by for a natural number .
finite ring: A finite set that contains and and over which a sum is explained that obeys the laws of associativity and commutativity.
In such a finite ring necessarily, every addition (and thus every multiplication and every raising to a power) has result . So the addition of is different from that on (or ). For example, for , We will introduce these finite rings first by the examples and , the rings given by the clock hours respectively weekdays), then for every .
When we look at the graphs of the functions, which are so regular on , we note that over the finite ring , either graph, that of
is initially as regular over as over , but starting
begins to behave erratically. (Except for the symmetry of the parabola on the central axis due to ).
Task. Experiment with the function plotter Grau (2018d) to view the erratic behavior of other function graphs over finite domains.
We apply modular arithmetic in everyday life when we add times in the daily, weekly and yearly cycle of clock hours, weekdays and months. It is this circularity that explains the naming “ring”.
The prototypical example of modular arithmetic is the arithmetic of the clock in which the pointer comes back to start after hours; formally, which implies, for example, That is, hours after hours is o’clock, and hours before o’clock is o’clock. We can go further: ; that is, if it is o’clock now, then in hours (one day later) as well.

Another example of modular arithmetic in everyday life are the days of the week: after days, the days of the week start over: If we enumerate ‘Saturday’, ‘Sunday’, ‘Monday’, ‘Tuesday’, ‘Wednesday’, ‘Thursday’ and ‘Friday’ by , , , , , , , then which implies, for example, Indeed, days after Wednesday is Sunday, and days before Sunday is Friday. We can go further: ; that is if now it is Thursday, then in days (two weeks later) as well.

Another example of modular arithmetic in everyday life are the months of the year: after months, the months of the year start over. If we number ‘January’, ‘February’, … for , , … then, as in the clock, which implies, for example, That is, a quarter after October the year starts over, and months before January is November. We can go further: ; that is, if it’s ‘May’ now, then in years as well.
Formally, we derive the equation Equation 5.1 from the equalities and In general, for every and in , or, equivalently, for all and in ,
Definition. Let and be positive integers. That divided by has remainder means that there is such an integer that
Example. For and , we compute . That is, the remainder of divided by is .
In other words, for every and in , if and only if and leave the same remainder divided by .
There is nothing special about the number (of clock hours). For example, analogous equalities would hold if the clock indicated hours (as many as a day on the planet Neptune has):

Definition. Let be a natural number. The integers and are congruent modulo , formally, if , that is, if their difference is divisible by . In other words, if and leave the same remainder divided by .
The number is called modulus.
Or, phrased differently, if and leave the same remainder divided by .
Congruence: Two integer and are congruent modulo if they leave the same remainder after division by .
Let us finally define these finite domains (the ring of integers modulo ) for a natural, usually prime, number , on which the trap-door functions in asymmetric cryptography live; those that make a cryptanalyst’s life so difficult when trying to compute their inverse (in contrast to the domains or ).
Given an integer , we want to define the ring (loosely, a set with an addition and multiplication governed by certain laws) such that More exactly, such a ring
If this equality for is to hold over , then the addition over has to be defined differently from that over . We put
That is, to add and multiply in ,
For example, for we get the addition and multiplication tables
| + | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
and
| * | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 0 | 2 |
| 3 | 0 | 3 | 2 | 1 |
Exercise. Show that an integer is divisible by (respectively ) if, and only if, the sum of its decimal digits is divisible by (respectively ).
In Python, the modular operator is denoted by the
percentage symbol %. For example, in the interactive shell,
we get:
>>> 15 % 12
3
>>> 210 % 12
6The base of and the exponent of determine whether the function is invertible or not.
The exponential function invertible if and only if it is onto, that is, every number, except is a value of the function. For example, for , the values are contained in :
Theorem on the existence of a primitive root. A generator of exists if, and only if,
A function (between a finite domain and counter-domain) is invertible if and only if it is injective, that is, sends different arguments to different values.
Task. Experiment with the function plotter Grau (2018d) to find examples of functions that are injective or not, that is, whose graph has two points at the same level.
If the exponent is even, for an integer , then raising to the power satisfies , that is, sends the arguments and to the same value. Thus, it is not injective. For example, for and , we observe this symmetry in Figure 5.3 along the central axis (but note that its restriction onto is injective).
Theorem. The raising to a power is injective over
RSA ) if and only if
has no common divisor with neither
nor
.Example. For example, for , the exponent gives the invertible function on .
What is the remainder of divided by ?
Because , it is .
Why is a number divisible by if and only if the sum of its decimal digits is divisible by ? Because , we have . Therefore, say . We have if and only if .
While the finite domains for a natural number complicate the computation of the inverse function of the trapdoor function, they actually facilitate the computation of the function itself given by the raising to a power:
RSA algorithm,
,
andGiven a base and an exponent in to calculate
expand the exponent in binary base, that is,
compute
Because , that is, each power is the square of the previous one (bounded by ), each power is, in turn, is easily computable.
raise to the power: Only powers equal to matter, the others can be omitted.
This algorithm takes module multiplications.
To calculate module , expand and calculate yielding:
To calculate module , expand and calculate yielding
Asymmetric cryptography relies on a trapdoor function, which
RSA ), butRSA ) must be practically incomputable without
knowledge of a shortcut, the key!This difficulty of calculating the inverse corresponds to the difficulty of decryption, that is, inverting the encryption. To complicate the computation of the inverse function (besides facilitating the computation of the proper function) is done using modular (or circular) arithmetic*, that we already know from the arithmetic of the clock, where is considered equal to .
Read the section on asymmetric cryptography in the article Simmons et al. (2016). Read in Menezes, Oorschot, and Vanstone (1997), Sections 2.4, 2.5 and 2.6 on the basic notions of number theory behind public key cryptography. Use Grau (2018d) to get an intuition for the graphs over finite domains.
See the book Sweigart (2013a) for implementing some simpler
(asymmetric) algorithms in Python, a readable
beginner-friendly programming language.
Read the parts of the book Schneier (2007) on understanding and implementing modern asymmetric cryptographic algorithms.
On completion of this chapter, you will have learned the Diffie-Hellman key exchange using the (Discrete) Logarithm.
In 1976, Whitfield Diffie and Martin Hellman conceived that the key distribution problem could be solved by an algorithm that satisfied:
(computationally) easy creation of a matched pair of keys for encryption and decryption,
(computationally) easy encryption and decryption,
(computationally) infeasible recovery of one of the keys despite knowledge of:
(computationally) infeasible recovery of the plaintext for almost all keys and messages .
Observation: This was the first public appearance of two-key cryptography. However, the British Government Communications Headquarters (GCHQ) knew it around a decade earlier.
RSA about three years before it was independently
developed by Rivest, Shamir, and Adleman, andThe first published protocol to overtly agree on a mutual secret key is the Diffie-Hellman key exchange protocol published in Diffie and Hellman (1976).
This is not yet two-key cryptography, because the single secret key
is known to both correspondents (in the following called Alice
and Bob). The asymmetric cryptographic algorithms that build on this
protocol (for example, ElGamal and ECC),
generate a unique key for every message.
Diffie-Hellman Key exchange: overt agreement on a common secret key whose security relies on the infeasibility of computing the logarithm modulo a large number.
Notation. Let us denote, in every asymmetric encryption algorithm,
For both correspondent, say Alice and Bob, to overtly agree on a secret key, they first combine
Then
CrypTool 1 offers in the menu entry
Individual Procedures -> Protocols a dialogue to
experiment with key values in the Diffie-Hellman.
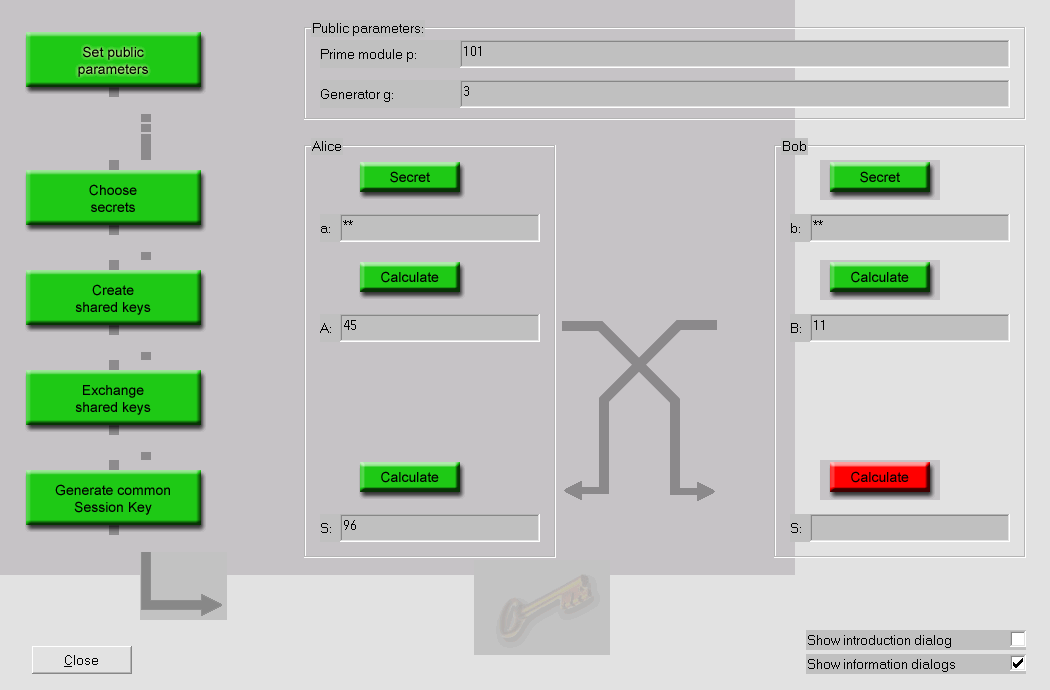
Observation. This protocol shows how to overtly build a
shared secret key. This key can then be used to encrypt all further
communication, for example, by an asymmetric algorithm such as
AES. However, the protocol shows
ElGamal (1985)
showed first how to build an encryption and signature algorithm on top
of the Diffie-Hellman protocol. While its encryption algorithm is rarely
employed (albeit, for example, the standard cryptography command-line
tool GnuPG offers it as first alternative to
RSA), its signature algorithm forms the basis of the
Digital Signature Algorithm (DSA), which is used in the US government’s
Digital Signature Standard (DSS), issued in 1994 by the National
Institute of Standards and Technology (NIST).
Elliptic Curve DSA (ECDSA) is a variant of the Digital Signature Algorithm (DSA) which uses points on finite (elliptic) curves instead of integers. The general number field sieve computes keys on DSA in subexponential time (whereas the ideal would be exponential time) . Elliptic curve groups are (yet) not vulnerable to a general number field sieve attack, so they can be (supposedly) securely implemented with smaller key sizes.
The security of the Diffie-Hellman key exchange is based on the difficulty of computing the logarithm modulo . An eavesdropper would obtain the secret key from and , if he could compute the logarithm as inverse of the exponentiation , that is While a power is easily computable (even more so using the fast power algorithm in Section 5.6), even more so in modular arithmetic, its inverse, the logarithm, the exponent for a given power, is practically incomputable for and appropriately chosen, that is:
the prime number
the powers , , … of the base generate a large set (that is, its cardinality is a multiple of ).
Let us look for such appropriate numbers:
Euclid’s Theorem. There are infinitely many prime numbers.
Demonstration: Otherwise, there are only finitely many prime numbers, say , …, are all of them. Consider . Since is greater than , …, , it cannot be prime. Let be a prime number that divides . Because , …, are prime, divides at least one of , …, . However, by its definition, has remainder divided by every prime , …, . The last two statements are in contradiction! Therefore, there must be an infinite number of primes.
Euclid’s Theorem. There are infinitely many prime numbers.
Euclid’s Theorem guarantees that there are arbitrarily many big prime numbers (in particular, bits).
Thank Heavens, for almost every prime number there is a prime number large ( bits) that divides .
The Theorem on the existence of a Primitive Root ensures that (since the modulus is prime) there is always a number in such that That is, every number , , , …, is a suitable power of . In particular, the cardinality of , , , …, is a multiple of any prime that divides . In practice, the numbers and are taken from a reliable source, such as a standards committee.
Since initially (for ) the values over equal to the values over , the secret numbers and should be large enough, that is, . To ensure this, in practice these numbers are artificially increased, that is, the message is padded.
At present, the fastest algorithm to calculate the logarithm from , is an adaption of the general number field sieve, see Gordon (1993), that achieves subexponential runtime. That is, roughly, the number of operations to calculate the logarithm of an integer of bits is exponential in
The Diffie-Hellman Key exchange protocol shows how to build overtly a
mutual secret key based on the difficulty of computing the logarithm
modulo
. This key can then be used to encrypt all further communication, for
example, by an asymmetric algorithm such as AES.
However, it shows
ElGamal (1985) showed first how to build an encryption and signature algorithm on top of the Diffie-Hellman protocol; in particular, it gave rise to the Digital Signature Algorithm, DSA.
Read in Menezes, Oorschot, and Vanstone (1997) Sections 3.1, 3.3 and try to understand as much as possible in 3.2 and 3.6 on the number theoretic problems behind public key cryptography.
Use CrypTool 1 to experiment with the
Diffie-Hellman protocol.
See the book Sweigart (2013a) for implementing some simpler
(asymmetric) algorithms in Python, a readable
beginner-friendly programming language.
Read the parts of the book Schneier (2007) on understanding and implementing modern asymmetric cryptographic algorithms.
On completion of this chapter, you will have learned …
what a trapdoor function is, and:
We study multiplication in the finite rings . We take a particular interest in what numbers we can divide into them. It will be the Euclid Algorithm that computes the answer for us.
The private key
RSA algorithm, orElGamal algorithm
(based on Diffie-Hellman key exchange),defines a function that is the inverse of the function defined by the public key. This inverse is computed via the greatest common divisor between the two numbers. This, in turn, is computed by Euclid’s Algorithm, an iterated division with rest.
We then introduce
Definition. A common divisor of two whole numbers and is a natural number that divides both and . The greatest common divisor of two whole numbers and is the greatest natural number that divides both and . Denote by the greatest common divisor of and ,
Example. The greatest common divisor of and is .
Iterated Division with rest yields an efficient algorithm to calculate the largest common divisor, Euclid’s Algorithm.
Definition. The integers and are relatively prime if , that is, if no integer divides and .
For all integer numbers and , integer numbers and for are relatively prime.
Division with rest helps us build an efficient algorithm to calculate the largest common divisor. Let us look back on Division with Rest:
Definition. Be and positive integer numbers. That divided by has quotient and rest means
Example. For and , we get . That is, the remainder of divided by is .
A linear combination (or sum of multiples) of two whole numbers and is a sum for whole numbers and .
Example. For and , a sum of multiples of them is
In particular, looking at the division with remainder in Equation 7.1, for an entire number , we observe:
That is, divides and if, and only if, divides and . That is, the common dividers of and are the same as those of and . In particular, By dividing the numbers and (which is ), we obtain e Iterating, and thus diminishing the remainder, we arrive at and with , that is
That is, the highest common divisor is the penultimate remainder (or the last one other than ).
Example. To calculate , we get
thus .
CrypTool 1, in the entry
Indiv. Procedures -> Number Theory Interactive -> Learning Tool for Number Theory,
Section 1.3, page 15, shows an animation of this
algorithm:
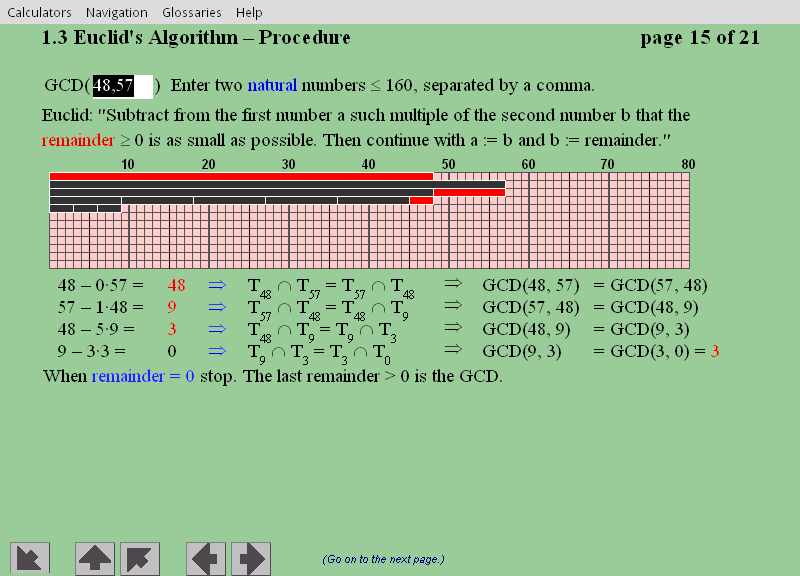
Theorem. (Euclidean algorithm) Let and be positive whole numbers with . The following algorithm calculates in a finite number of steps:
(start) Put and , and .
(division) Divide by with rest to get Then
Demonstration: We need to demonstrate that the algorithm ends with the highest common divisor of and :
Like , finally for large enough, and the algorithm ends.
For Equation 7.1, we have As ultimately for big enough, we have That is, .
Observation: All it takes is divisions with rest for the algorithm to finish.
Demonstration: We demonstrate We have
In the latter case, it follows and then For () we get iteratively that just divisions with rest for the algorithm finish.
In fact, it turns out that a factor of is enough with rest, and on average is enough .
For the computation of the exponent of the decryption function, we need more information than the largest common divisor (calculated by the Euclid Algorithm). In fact, one observes (Euclid’s Extended Algorithm) that in each step of the Euclid’s Algorithm the largest common divisor of and is a linear combination (or sum of multiples) of and , that is, The inverse of modulo is one of these multiples:
Example. For and , a sum of multiples of them is
Theorem. (Euclid’s Extended Algorithm) For any positive integers and , their highest common divisor is a linear combination of and ; that is, there are integers and such that
CrypTool 1, in the
Indiv. Procedures -> Number Theory Interactive -> Learning Tool for Number Theory,
Section 1.3, page 17, shows an animation of this
algorithm:
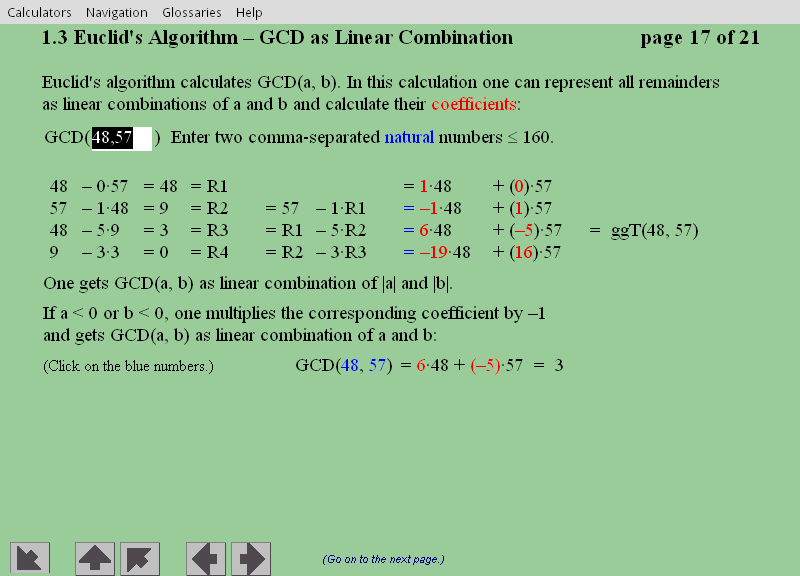
Example. We have and, indeed,
Demonstration: As , , and , it follows that is a linear combination of and . In general, since and are linear combinations of and , first is a linear combination of and , and so is a linear combination of and . In particular, if then is a linear combination of and .
CrypTool 1, in the menu entry
Indiv. Procedures -> Number Theory Interactive -> Learning Tool for Number Theory,
Section 1.3, page 17, shows an animation of this
algorithm:

Example. Let’s review the calculation of the largest common divisor of and . Euclid’s algorithm did:
,
which provides the linear combinations
.
Indeed,
PythonTo implement the Euclid algorithm, we will use multiple assignment in
Python:
>>> spam, eggs = 42, 'Hello'
>>> spam
42
>>> eggs
HelloThe names of the variables and their values are listed to the left of respectively.
Here is a function that implements the Euclid algorithm in
Python; it returns the largest common divisor
of two whole
and
.
def gcd(a, b):
while a != 0:
a, b = b % a, a
return bFor example, in the interactive shell:
>>> gcd(24, 30)
6
>>> gcd(409119243, 87780243)
6837The // operator will figure in the implementation of the
extended Euclid algorithm; it divides two numbers and rounds down. That
is, it returns the greater integer equal to or less than the result of
the division. For example, in the interactive shell:
>>> 41 // 7
5
>>> 41 / 7
5.857142857142857
>>> 10 // 5
2
>>> 10 / 5
2.0We chose the following implementation of the extended Euclid algorithm:
def egcd(a, b):
x,y, u,v = 0,1, 1,0
while a != 0:
q, r = b//a, b%a
m, n = x-u*q, y-v*q
b,a, x,y, u,v = a,r, u,v, m,n
gcd = b
return gcd, x, yThe private key is calculated by the multiplicative reverse
in the modular arithmetic from the public key, both in the
RSA algorithm and the ElGamal algorithm.
We have just learned how to calculate the largest common divisor by the Euclid Extended Algorithm; we now learn how it is used to calculate this multiplicative reverse.
While in we can divide by any number (except ), in only by ! The numbers you can divide by are called invertible or units. The amount of invertible numbers in depends on the module. Roughly speaking, the fewer prime factors in , the more units in .
Definition. The element in is a unit (or invertible) if there is in such that . The element is the inverse of and denoted by . The set of units (where we can multiply and divide) is denoted by Euler’s totiente function # is that is, given , it counts how many units has.
Examples:
On the clock, that is, for the multiplication of one hour by corresponds to iterate times the path taken by the indicator in (from .) We note that for and there is a iteration of the path that leads the indicator to (more exactly made , , and times), while for all other numbers this iteration leads the indicator to . These possibilities are mutually exclusive, and we conclude That’s .
On days of the week, that is, for , we get That is, the number of units is as large as possible, that is, , all numbers except .
For , the multiplication table
| * | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 0 | 2 |
| 3 | 0 | 3 | 2 | 1 |
shows because and in . In contrast, in , in particular is not a unit. (But a zero divisor; in fact, each element in is either a unit, or a zero divider). Thus .
For , the multiplication table
| * | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
reveals the units .
Proposition. Let and in , that is, in . The number is a unit in if, and only if, .
Demonstration: We observe that each common divisor of and divides each sum of multiple of and ; in particular, if , then the largest common divisor of and is .
By the Extended Euclid Algorithm, there is and in such that So, from the above observation, if, and only if, there is in such that That is, is a unit in whose inverse is .
Observation. We concluded that for in with , we obtained by the Extended Euclid Algorithm and in such that The reverse of in is given by the remainder of divided by .
In Python, we can then calculate the inverse of
in
by
def ModInverse(a, m):
if gcd(a, m) != 1:
return None # no mod. inverse exists if a and m not rel. prime
else
gcd, x, y = egcd(a,m)
return x % mWhat mathematical function is used to encrypt in
RSA? Raising to a power modulo a composed
integer.*
What mathematical function is used to decrypt in
RSA? Taking a root modulo a composed
integer.
What is a principal use of RSA on the Internet
today? The verification of certificates.
Asymmetric cryptography relies on a trapdoor function, which
RSA ), butRSA ) must be practically incomputable without
knowledge of a shortcut, the key!This difficulty of calculating the inverse corresponds to the difficulty of decryption, that is, inverting the encryption. To complicate the computation of the inverse function (besides facilitating the computation of the proper function) is done using modular (or circular) arithmetic*, that we already from the arithmetic of the clock, where is considered equal to .
Read the section on asymmetric cryptography in the article Simmons et al. (2016). Read in Menezes, Oorschot, and Vanstone (1997), Sections 3.1, 3.3 and try to understand as much as possible in 3.2 and 3.6 on the number theoretic problems behind public key cryptography
Use CrypTool 1 to experiment with Euclid’s
algorithm.
See the book Sweigart (2013a) for implementing some simpler
(asymmetric) algorithms in Python, a readable
beginner-friendly programming language.
Read the parts of the book Schneier (2007) on understanding and implementing modern asymmetric cryptographic algorithms.
On completion of this chapter, you will have learned …
what a trapdoor function is, and:
the most common asymmetric cryptographic algorithms and their underlying trapdoor functions:
RSA Algorithm using the (discrete) Power
Function.The best-known public-key algorithm is the Rivest-Shamir-Adleman (RSA) cryptoalgorithm from Rivest, Shamir, and Adleman (1978). A user secretly chooses a pair of prime numbers and so large that factoring the product is beyond estimated computing powers for the lifetime of the cipher. The number will be the modulus, that is, our trapdoor function will live on .
RSA: algorithm that encrypts by raising to a power and whose security relies on the computational infeasibility of factoring a product of prime numbers.
is public, but
and
are not. If the factors
and
of
were known, then the secret key can be easily computed. For
RSA to be secure, the factoring must be computationally
infeasible; nowadays 2048 bits. The difficulty of factoring
roughly doubles for each additional three digits in
.
Having chosen and , the user selects any integer e less than n and relatively prime to and , that is, so that is the only factor in common between e and the product . This assures that there is another number d for which the product ed will leave a remainder of when divided by the least common multiple of and . With knowledge of and , the number d can easily be calculated using the Euclidean algorithm. If one does not know and , it is equally difficult to find either or given the other as to factor , which is the basis for the cryptosecurity of the RSA algorithm.
The RSA algorithm creates
Compared to the Diffie-Hellman protocol, it has the
advantage that it is completely asymmetric: there is no need to share a
mutual secret key (and therefore the secret key is kept in a single
place only, but not two). Instead a single correspondent has access to
the secret key. However, in this case the communication is encrypted
only towards the owner of the secret key. To encrypt in both
directions,
RSA
key,The keys for encrypting, and decryption, , will be constructed via Euler’s Formula, which in turn is based on Fermat’s Little Theorem.
Fermat’s Little Theorem. If is a prime number, then for any integer ,
In particular, for every integer ,
For example, if , that is, and are such that (so to speak, ) then that is, That is, the computation of the -th root is equal to that of the -th power , a great computational shortcut! The existence of such a shortcut given is assured by Euler’s formula:
Theorem. (Euler’s formula) Let and be different prime numbers. If is divisible by neither nor , then
Proof: By Fermat’s Little Theorem, and that is, and divide . Since and are different prime numbers, divides , that is, .
Corollary. (Taking roots modulo N) Let and be different prime numbers, and . For every exponent such that we have
Demonstration: If or divides , then . Otherwise, we can apply Euler’s Formula: Because , that is, there is such that , by Euler’s Formula,
Observation (crucial for the RSA algorithm). If
, then by Euler’s Formula
, that is, taking to the power is the identity function,
In particular, if
is the product of two whole numbers
and
, that is,
then
That is,
. Calculating a power is much easier than a root!
Example. If and then If and , then . For example, for base , we check and That is,
(Recall that an upper case letter denotes a public number (and vice-versa), whereas a lower case letter denotes a secret number.) For Alice to secretly send the message to Bob through an insecure channel:
Bob, to generate the key, chooses
Bob, to transmit the key, sends to Alice
Alice, to cipher,
Bob, to decipher,
Computing
by knowing both prime factors of
is Bob’s shortcut. CrypTool 1 offers in the menu
Individual Procedures -> RSA Cryptosystem the entry
RSA Demonstration to experiment with different values of
the key and message in RSA.
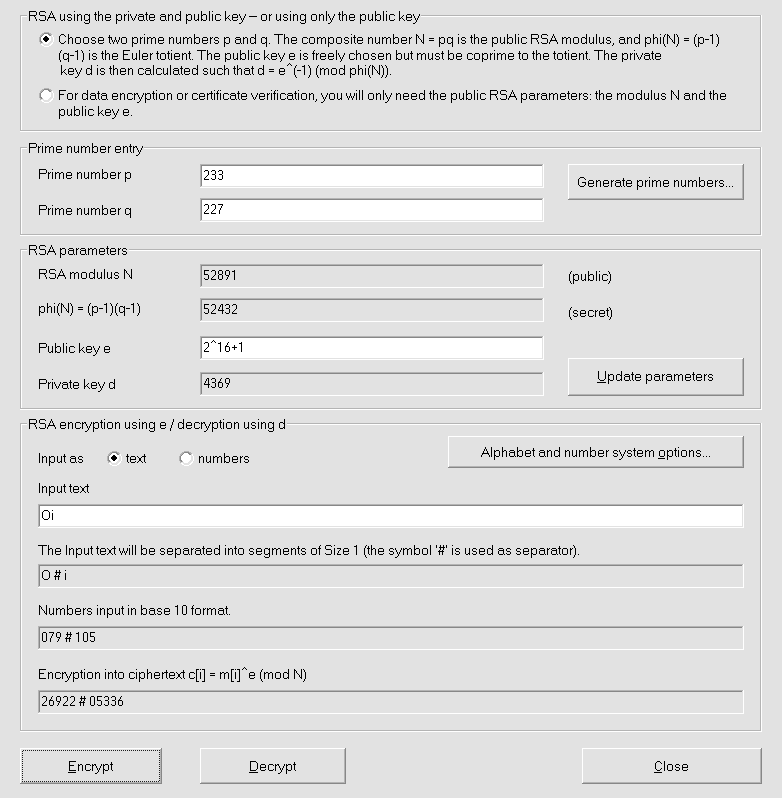
In sum, raising to the power encrypts where the exponent is the public key. Correspondingly, its inverse, taking the -th root , decrypts. It is practically incomputable. However, modulo , by Euler’s formula, there is such that for a number that Euclid’s Algorithm calculates from as well as and . Therefore, the secret key is , or, sufficiently, the knowledge of the prime factors and of .
Since
are all public, the computational security of
RSA is solely based on the difficulty of finding a root
modulo a large number
An eavesdropper would obtain the secret message from , and only if he could compute
The shortcut is the knowledge of the two prime factors and of that makes it possible to calculate
so that, by the Euler Formula, .
Euclid’s Theorem guarantees that there are arbitrarily large prime numbers (in particular, bits). While taking powers is computationally easy, taking roots is computationally hard for suitable choices of and , that is, for large enough prime numbers and (while the choice of the exponent is free; for example, ):
The fastest algorithm to calculate the prime factors
and
from
is the general number sieve, see A. K. Lenstra et al. (1993).
The number of operations to factor an integer number of
bits is roughly
Therefore, according to Barker (2016), the National Institute for
Standards and Technology (NIST)
In practice, the plaintext number needs to be padded, that is, the number randomly increased. Otherwise, when the plaintext number and the exponent are both small (for example, ), then possibly the enciphered message satisfies . In this case, the equality So is easily computable, for example, by the Bisection method already presented, (or, numerically more efficient, by Newton’s method).
A simple hypothetical attack is that by Wiener when
If the conditions of the theorem are met, then the secret can be computed by a linear time algorithm as the denominator of a continuous fraction.
Observation. If (but not ) is too small, then an attack is much more difficult; see Boneh et al. (1999).
RSA is still a standard of many asymmetric cryptographic
methods. One principal use of RSA nowadays lies in the
verification of (older) certificates emitted by certificate authorities.
See Section 13.
Other uses are that by GPG for asymmetric cryptography,
such as the OpenPGP protocol to encrypt e-mail messages,
which creates RSA keys by default:
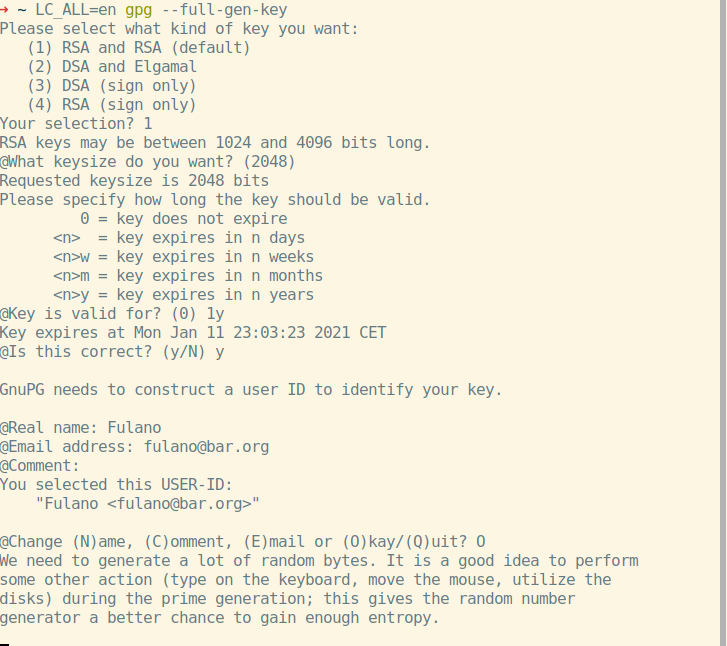
The command line program GPG creates keys and makes it
possible to (de)encrypt and sign/authenticate with them. Other
(graphical) applications, for example, the Enigmail
extension for the free e-mail client Thunderbird, use it
for all these cryptographic operations.
RSA?
Raising to a power modulo a composed integer.RSA?
Taking a root modulo a composed integer.RSA on the Internet today?
The verification of certificates.Let us recall that in public-key cryptography there are two keys, a public key and a private key. Usually:
Thus, a text can be transferred from the encipherer (Alice) to one person only, the decipherer (Bob). The roles of the public and private keys can be reversed:
Thus, the encipherer can prove to all decipherers (those who have the public key) his ownership of the private key; the digital signature.
digital signature: encryption of a message by the private key followed by decryption by the public key to check whether the original message was encrypted by the private key.
The theory (meaning the mathematics) behind the encryption by the
public key (digital messages) or private key (digital signature) is
almost the same; only the roles of the trap function arguments are
reversed. (For example, in the RSA algorithm, this exchange
of variables is indeed all that happens). In practice, however, usually
encrypted by the private key are:

That is, while
In the RSA Signature Algorithm, to sign (instead of encrypt), the only difference is that the exponents and exchange their roles. That is, the signed message is (instead of ). For Samantha to sign the message and Victor to verify it,
Samantha, to generate a signet, chooses
Samantha, to transmit the signet, sends to Victor
Samantha, to sign,
Victor, to verify, calculates (which holds by Euler’s Formula).
Observation. Signing and the deciphering are both given by for the private key . So, signing an encrypted document (for the public key that corresponds to ) is equivalent to deciphering it! Therefore, in practice,
different key pairs are used
a cryptographic hash of the document is signed, a small number that identifies the document.
CrypTool 1 offers in the menu
Individual Procedures -> RSA Cryptosystem the entry
Signature Generation to experiment with different values of
the signature and the message.
We note that instead of the original message, it signs:
a cryptographic hash (for example, by the algorithm
MD5) of the original message, and
with additional information, such as
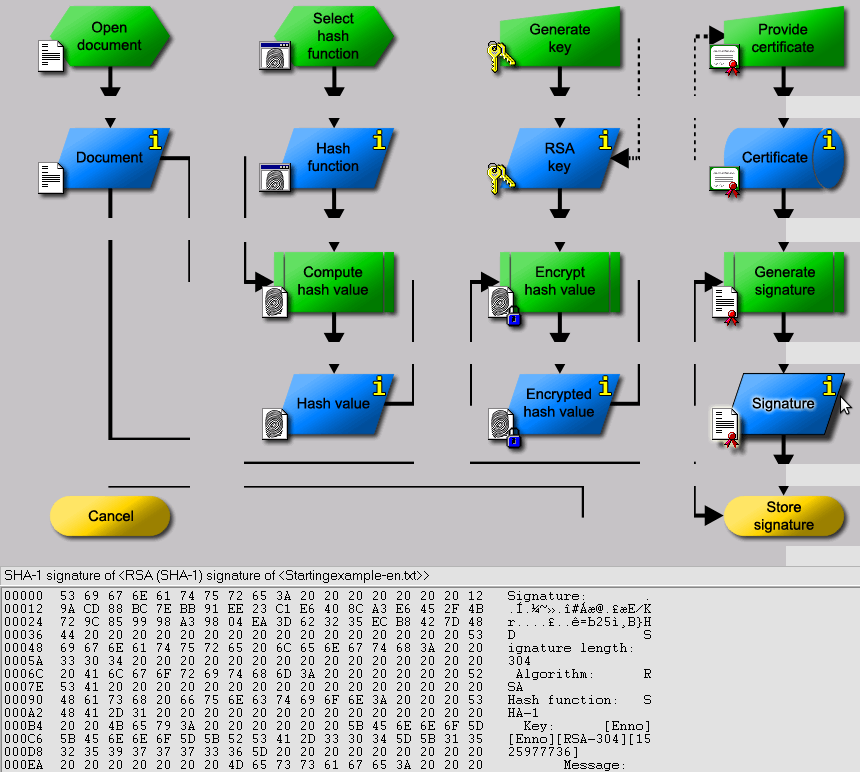
ElGamal (1985)
showed first how to build an encryption and signature algorithm on top
of the Diffie-Hellman protocol. While its encryption algorithm is rarely
employed (albeit, for example, the standard cryptography command-line
tool GnuPG offers it as a first alternative to
RSA), its signature algorithm forms the basis of the
Digital Signature Algorithm (DSA), which is used in the US government’s
Digital Signature Standard (DSS), issued in 1994 by the National
Institute of Standards and Technology (NIST). Elliptic Curve DSA (ECDSA)
is a variant of the Digital Signature Algorithm (DSA) which uses points
on finite (elliptic) curves instead of integers.
Single-key (or symmetric) cryptography suffers from the key distribution problem: to pass the same secret key to all, often distant, correspondents. Two-key (or asymmetric) cryptography solves this problem seemingly at once, by enabling the use of different keys to encrypt and decrypt. However, the identity of the key owner must be confirmed; if not personally, then by third parties, that is, identities with private keys that confirm by their digital signatures that it is Alice who owns the private key. However, the problem of the public key identity arises again: How can we ensure the identities of these private key owners? There are two solutions: In the approach via hierarchical authorities, private key owners are distinguished by hierarchical levels. At the highest level lie the root authorities on which one trusts unconditionally. In the web of trust, trust is transferred from one to the other, that is, trust is transitive: If Alice trusts Bob, and Bob trusts Charles, then Alice trusts Charles.
Asymmetric cryptography relies on a trapdoor function, which
RSA ), butRSA ) must be practically incomputable without
knowledge of a shortcut, the key!This difficulty of calculating the inverse corresponds to the difficulty of decryption, that is, inverting the encryption. To complicate the computation of the inverse function (besides facilitating the computation of the proper function) is done using modular (or circular) arithmetic*, that we already from the arithmetic of the clock, where is considered equal to .
The Diffie-Hellman Key exchange protocol shows how to build overtly a
mutual secret key based on the difficulty of computing the logarithm
modulo
. This key can then be used to encrypt all further communication, for
example, by an asymmetric algorithm such as AES.
However, it shows
ElGamal (1985) showed first how to build an encryption and signature algorithm on top of the Diffie-Hellman protocol; in particular, it gave rise to the Digital Signature Algorithm, DSA.
The best-known public-key algorithm is the Rivest-Shamir-Adleman
(RSA) cryptoalgorithm. A user secretly chooses a pair of
prime numbers
and
so large that factoring the product
is beyond estimated computing powers during the lifetime of the cipher;
The number
will be the modulus, that is, our trapdoor function will be defined on
.
is public, but
and
are not. If the factors
and
of
were known, then the secret key can be easily computed. For
to be secure, the factoring must be computationally infeasible; nowadays
2048 bits. The difficulty of factoring roughly doubles for
each additional three digits in
.
To sign (instead of encrypt), the only difference is that the exponents and exchange their roles. That is, the signed message is (instead of ):
The trapdoor function of of RSA is raising to a power,
for a message
, and its computational security relies upon the difficulty of finding a
root modulo a large number
The shortcut is the knowledge
of the two prime factors
and
of
that makes it possible to calculate the inverse multiplicative
of
, that is,
such that
Then
computing a power is a lot faster than
a root.
What is the inverse of the trapdoor function used in RSA?
What is the fastest known algorithm to attack
RSA?
What is the minimum key size of RSA to be currently considered secure, for example, by the NIST?
Read the section on asymmetric cryptography in the article Simmons et al. (2016). Read in Menezes, Oorschot, and Vanstone (1997),
Use Grau (2018d) to get an intuition for the graphs over finite domains.
Read Chapter 10 on RSA.
Use CrypTool 1 to experiment with RSA.
See the book Sweigart (2013a) for implementing some simpler
(asymmetric) algorithms in Python, a readable
beginner-friendly programming language.
Read the parts of the book Schneier (2007) on understanding and implementing modern asymmetric cryptographic algorithms.
Let us recall Euclid’s Theorem which asserts that there are prime
numbers arbitrarily large (for example, with
binary digits for the RSA):
Euclides’ theorem. There are infinitely many prime numbers.
Demonstration: Let’s suppose otherwise, that there’s only a finite number of prime numbers. Consider Since is greater than , …, , it is not prime. So let be a prime number that divides . Therefore, must be one of , …, . But, by its definition, leaves rest for any , …, .
Contradiction! So there’s no greatest prime number. q.e.d.
Marin Mersenne (Oizé, 1588 — Paris, 1648) was a French Franciscan friar who tried to find, without success, a formula to give all prime numbers. Motivated by a letter from Fermat in which he suggested that all the numbers , Fermat’s Numbers be primes, Mersenne studied the numbers of the form In 1644 he published the work Cogita physico-mathematica which states that these numbers are primes for (and mistakenly included and ). (Only a computer could show in that is composed.)
Mersenne’s prime numbers, in the form of to prime, are known to be
, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , e
The prime number has digits. It was found on December 8,2018 and is to this day the biggest known prime number.
“CrypTool 1”, in the menu entry “Indiv. Procedures -> Number Theory Interactive -> Compute Mersenne Numbers’ allows you to calculate some of Mersenne’s prime numbers.
A quick test if the natural number is compound is the Small Fermat Theorem (formulated as its contraposition): If there is a natural number such that then is compound.
But the reverse implication doesn’t hold: There are numbers (which are called Carmichael numbers) that are compound but for every natural number , The lowest such number is (which is divisible by ).
The simplest algorithm to verify whether a number is prime or not is the Eratosthenes sieve (285 – 194 B.C.).

To illustrate this, let’s determine the prime numbers between and .
Initially, we’ll determine the largest number by what we’ll divide to see if the number is composed; is the square root of the upper coordinate rounded down. In this case, the root, rounded down, is .
The next number on the list is prime. Repeat the procedure:
As initially determined, is the last number we divide by. The final list , , , , , , , , , contains only prime numbers.
Here’s an implementation in Python:
def primeSieve(sieveSize):
# Returns a list of prime numbers calculated using
# the Sieve of Eratosthenes algorithm.
sieve = [True] * sieveSize
sieve[0] = False # zero and one are not prime numbers
sieve[1] = False
# create the sieve
for i in range(2, int(math.sqrt(sieveSize)) + 1):
pointer = i * 2
while pointer < sieveSize:
sieve[pointer] = False
pointer += i
# compile the list of primes
primes = []
for i in range(sieveSize):
if sieve[i] == True:
primes.append(i)
return primesThe test of AKS determines in
polynomial time whether
is compound or prime (more exactly, in time
where
= the number of digits
[binary] of
).
In practice, the Miller-Rabin test is usually enough to
guarantee much more witnesses (=
numbers that prove whether
is composed or not) than Fermat’s Little Theorem.
In fact, when we compare the duration between the two algorithms to
check if a number is prime on a computer with a 2GHz
Intel Pentium-4 processor, we get
| prime number | Miller-Rabin | AKS |
|---|---|---|
The CrypTool 1 offers in the
Individual Procedures -> RSA Menu an entry to experiment
with different algorithms to detect prime numbers.
Miller-RabinThe simplistic tests, to know if a number is prime or not, are inefficient because they calculate the factors. Instead of them, to know only if it is prime or not, there is the Miller-Rabin Test. After your demonstration, we’ll give you your opposition; it’s in this formulation that it’s applied.
The Miller-Rabin Test. Be a prime number, be for numbers and (with odd). So, for any whole number indivisible for is worth
Demonstration: By the Little Theorem of Fermat By iteratively extracting the square root, we obtain
If for an odd number, a possibly prime number, we write , then by Fermat’s Test is not prime if there is a whole such that . The Miller-Rabin Test explains the condition :
The Miller-Rabin Test. (Contraposition) It’s odd and for numbers and (with odd). An integer relatively prime to is a Miller-Rabin Witness (for divisibility) of , if
Question: What are the chances that we declare by the Miller-Rabin Test accidentally a prime number, that is, a number that is actually compound?
Theorem. (About the frequency of witnesses) Be odd and compound. So at least of the numbers in , …, are Miller-Rabin Witnesses for .
So, already after attempts , , …, without witness we know with a chance , that the number is prime!
Let’s implement
# Primality Testing with the Rabin-Miller Algorithm
# http://inventwithpython.com/hacking (BSD Licensed)
random import
def rabinMiller(num):
# Returns True if num is a prime number.
s = num - 1
t = 0
while s % 2 == 0:
# keep halving s while it is even (and use t
# to count how many times we halve s)
s = s // 2
t += 1
for trials in range(5): # try to falsify num's primality 5 teams
a = random.randrange(2, num - 1)
v = pow(a, s, num)
if v != 1: # this test does not apply if v is 1.
i = 0
while v != (num - 1):
if i == t - 1:
return False
else:
i = i + 1
v = (v ** 2) % in a
return Truedef isPrime(num):
# Return True if num is a prime number. This function does a
# quicker prime number check before calling rabinMiller().
if (num < 2):
return False # 0, 1, and negative numbers are not prime
# About 1/3 of the time we can quickly determine if num is not
# prime by dividing by the first few dozen prime numbers.
# This is quicker # than rabinMiller(), but unlike rabinMiller()
# is not guaranteed to prove that a number is prime.
lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107,
109, 113, 127, 131, 137, 149, 151, 157, 163, 167, 173, 179, 181,
191, 193, 197, 199, 211, 223, 227, 233, 239, 241, 251, 257, 263,
269, 271, 277, 281, 283, 293, 307, 311, 313, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 431, 433,
439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509,
523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607,
613, 617, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691,
701, 709, 719, 727, 739, 743, 751, 757, 761, 769, 773, 787, 797,
809, 811, 821, 823, 827, 829, 853, 857, 859, 863, 877, 881, 883,
887, 907, 911, 919, 929, 937, 941, 947, 967, 971, 977, 983, 991,
997]
if in a lowPrimes:
return True
# See if any of the low prime numbers can divide into one
for prime in lowPrimes:
if (num % prime == 0):
return False
# If all else fails, call rabinMiller() to check if num is a prime.
return rabinMiller(num)def generateLargePrime(keysize = 1024):
# Return a random prime number of keysize bits in size.
while True:
num = random.randrange(2**(keysize-1), 2**(keysize))
if isPrime(num):
return numLet’s observe for modules that are not primes, that is, a product of primes factors, that the difficulty increases linearly in the number of factors, unlike it increases exponentially in the number of bits of each factor:
If the module is the product of two factors and without common factor, then the modular logarithm can be computed, by the Chinese Theorem of the Remains, by the logarithms More exactly, there are integers and , computed (in linear time in the number of and bits) by the Euclid Algorithm (extended), such that and
If the modulus is a power of a prime , then Bach (1984) shows how the modular logarithm module for a base can be computed in polynomial time from the module logarithm. Let’s expose the steps to a prime number :
We conclude that, given
the value of of is computed in polynomial time.
Observation. To facilitate computing, instead of projection given in for , it’s faster to use that given in by . However, its restriction is not identity. So you need to use it instead of the scaled logarithm in order to obtain
Let’s explain Equation 9.1 which defines the logarithm : let us remember the definition of the exponential on for compound interest which leads to the definition of the inverse function where .
Now, at , we have , , , , …, , that is, , which may motivate the idea of considering as small. So, the good analog about is In fact, over , is a well defined value in , because if divides , then no denominator of the fraction cut is divisible by and all indivisible numbers by are invertible by . Likewise, over , is a well defined value at , because if divides , then no cut denominator is divisible by and all indivisible numbers by are invertible by .
Of particular interest is the base of the natural logarithm at , that is, the argument such that . For example, for and , we calculate
Asymmetric cryptography relies on a trapdoor function, which
RSA ), butRSA ) must be practically incomputable without
knowledge of a shortcut, the key!This difficulty of calculating the inverse corresponds to the difficulty of decryption, that is, inverting the encryption. To complicate the computation of the inverse function (besides facilitating the computation of the proper function) is done using modular (or circular) arithmetic*, that we already from the arithmetic of the clock, where is considered equal to .
Use CrypTool 1 to experiment with various prime
detection algorithms.
On completion of this chapter, you will have learned …
Denote . Among all curves, the clou of the elliptic curves (given by an equation ) is that one can add points on them: if a line passes for and . By restricting the solutions to points in for a large prime number and fixing a point on the curve,
Diffie-Hellman over Elliptic Curves: (an analog of) the Diffie-Hellman protocol, in which iterated multiplication of a number modulo is replaced by iterated addition of a point on a finite elliptic curve.
The Diffie-Hellman protocol (over
)
has an analog over Elliptic Curves:
The advantage of using
is that depending on the number of bits of (regarding the fastest presently known algorithms):
For example, the security obtained by a 2048 bits key
for the multiplicative logarithm equals approximately that of a
224 bits key for the logarithm over an elliptic curve. To a
length of 512 bits of a key for an elliptic curve,
corresponds a length of 15360 bits of an RSA
key.
In the next sections, we:
We realized that we already use the modular arithmetic in everyday life, for example for the modulus , the arithmetic of the clock, and for , the days of the week. More generally, we defined, for any integer the finite ring (= a finite set where we can add and multiply), roughly,
If is prime, then it can be shown that is a field denoted by : for every in , except , there is always in , the inverse multiplicative of defined by satisfying . In other words, in a field we can divide by every number except . (The most common examples are the infinite fields and .)
for : A ring of polynomials with coefficients in of degree
In cryptography, elliptic curves are defined over fields whose cardinality is a power of a prime number (and not just till now); for example, for a large number . The case is particularly suitable for computing (cryptographic). The fields of the form are called binary.
In Section 2.4, we already made acquaintance with the Rijndael field, which was defined by polynomials of degree with binary coefficient. More generally, the field to is defined by polynomials of degree over ,
The addition of two polynomials is the addition of polynomials, that is, the coefficient to coefficient addition in , and
to multiply two polynomials,
For example, for
with
and
, we get the field
used in AES . As a set
that is, the finite sums
for
,
,
…,
in
.
An elliptic curve over a finite field (in which ) is an equation for coefficients and such that the curve is not singular, that is, its discriminant is nonzero, .
Note.
The equation is the form of Weierstraß, but there are several others that have proved to be computationally more efficient, such as that of Montgomery
If the characteristic is , that is, with , then the equation is .
After choosing a domain (for example, , , , or for a prime number ) the points that solve this equation, , form a curve in the plane. This plane,
In addition to the points in the plane, there is also the point at infinity (or ideal point) that is denoted . Thus, the points of the elliptic curve are given by where the notion of point depends on the domain: On a finite field , the number of points is limited by where , that is, asymptotically equal to . It can be computed by Schoof’s algorithm Schoof (1995) in about operations for the number of binary digits of .
Just as the coefficients and , this plane can be a rational, real, complex or finite plan, that is, a finite field for a power of a prime number .
For the domain , the curves take the following forms in the real plane for different and parameters:
While on finite fields, we obtain a discrete set of points (symmetrical around the middle horizontal axis).
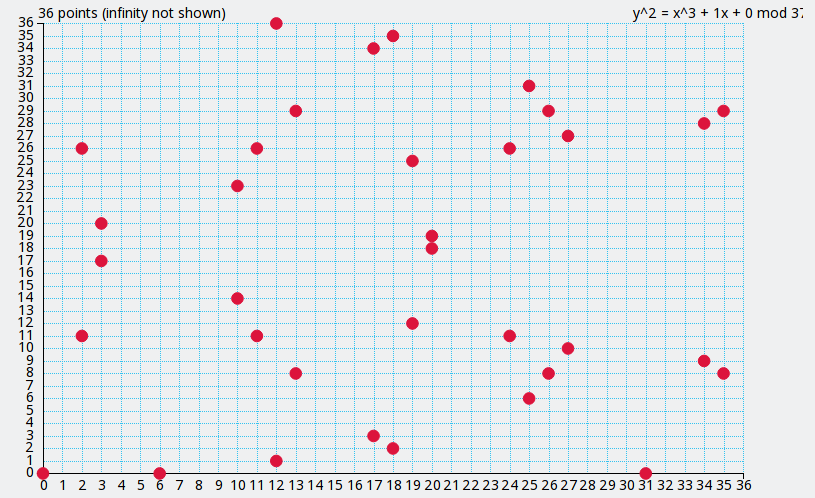
For the cryptographic algorithm on this curve to be safe, that is, the computation of the logarithm on it takes time, there are restrictions on the choices of and the elliptic curve (that is, on its defining coefficients and ). For example,
that the coefficients and are such that
The probability that a randomly generated curve (that is, one whose coefficients and in the equation are randomly generated) is vulnerable to one of these attacks is negligible.
Ideally, these choices are publicly justified.
A safe choice is for example: The Curve25519 given by
over
with
where
(which explains its name); its number of points is
. (This curve became popular as an unbiased alternative to the
recommended, and soon distrusted, curves by the National Institute for
Standards and Technology, NIST).
nistk163,
nistk283, nistk571 and nistb163,
nistb283, nistb571 defined over the binary
field with 163, 283 and 571
bits.Brainpool P256r as specified
in the RFC7027 used to encrypt the data on the German
microchip ID card.To ensure that the coefficients are not chosen to intentionally compromise cryptographic security, they are often obtained at random, that is,
SHA-256.How is the sum of two points on an elliptic curve defined? Geometrically the sum of three points , and on an elliptic curve in the Euclidean plane (that is, in ) is defined by the equality if a line passes and . However, over finite fields, this geometric intuition no longer applies, and we need an algebraic definition (which is also the form that the computer expects).
If we look at the real points of the curve , that is, at all the points in such that , the addition has a geometric meaning: We have if , and are on the same line. More exactly:
The reflection of along the -axis is the point .
CrypTool 1 demonstrates this geometric addition in an
animation accessible from the
Point Addition on Elliptic Curves entry in the menu
Procedures -> Number Theory - Interactive.
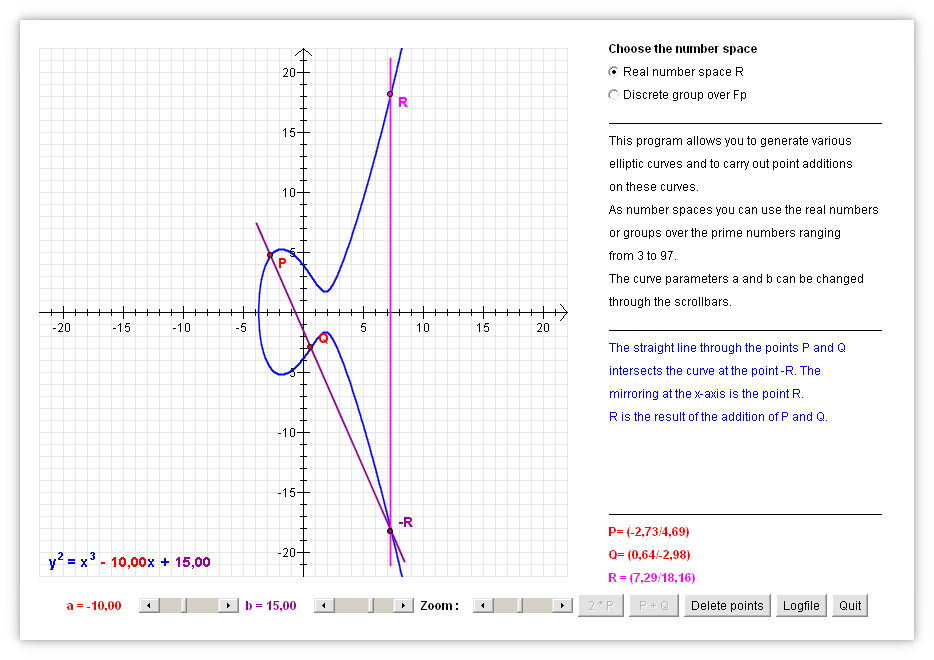
This geometric description of the addition leads us to the following algebraic description: Expressed by Cartesian coordinates, the addition of two points of an elliptic curve is given by an algebraic formula, that is, it involves only the basic operations of addition, multiplication (and raising to a power). (Thus, we can replace the unknowns by values in any domain, be it , , or .)
Proposition: Denote by If the curve is given by and the points , and are non-zero, then where is the degree of inclination of the line that passes through and given by
Demonstration: For a cubic curve not in the normal Weierstrass shape, we can still define a group structure by designating one of its nine inflection points as the identity. On the projective plane, each line will cross a cubic at three points when considering multiplicity. For a point, is defined as the third exclusive point in the line passing and . So for all and , + is defined as where is the third exclusive point in the line containing and .
Be a field on which the curve is defined (that is, the coefficients of the equation or defining equations of the curve are in ) and denotes the curve as . So, the rational points are the points whose coordinates are in , including the point at infinity. The -rational points set is indicated by ( ). It also forms a group, because the properties of the polynomial equations show that if is in ( ), then is also in ( ), and if two of , and are in ( ), then it is the third. Also, if is a subfield of , then ( ) is a subgroup of ( ). Given the curve on the field (such that ), and the points = (, ) and = (, ) on the curve.
If , then the Cartesian equation of the line intersecting and with the slope For the values , and the equation of the line is equal to the curve or, equivalently, The roots of this equation are exactly , and ; thence
Therefore, the coefficient of gives the value ; the value of follows by replacing in the Cartesian equation of the line. We conclude that the coordinates (, ) = = -( + ) are
If = , then
Observation. For certain specific curves, these formulas can be simplified: For example, in an Edwards’ Curve of the shape for (with neutral element the point ), the sum of the points and is given by the formula (and the inverse of a point is ). If is not a square in , then there are no exceptional points: The denominators and are always different from zero.
If, instead of , we look at the points with entries in a finite field from the curve , that is, all points in such that , the addition is uniquely defined by the formula .
CrypTool 1 demonstrates this addition in the entry
Point Addition on Elliptic Curves of the menu
Indiv. Procedures -> Number Theory - Interactive.
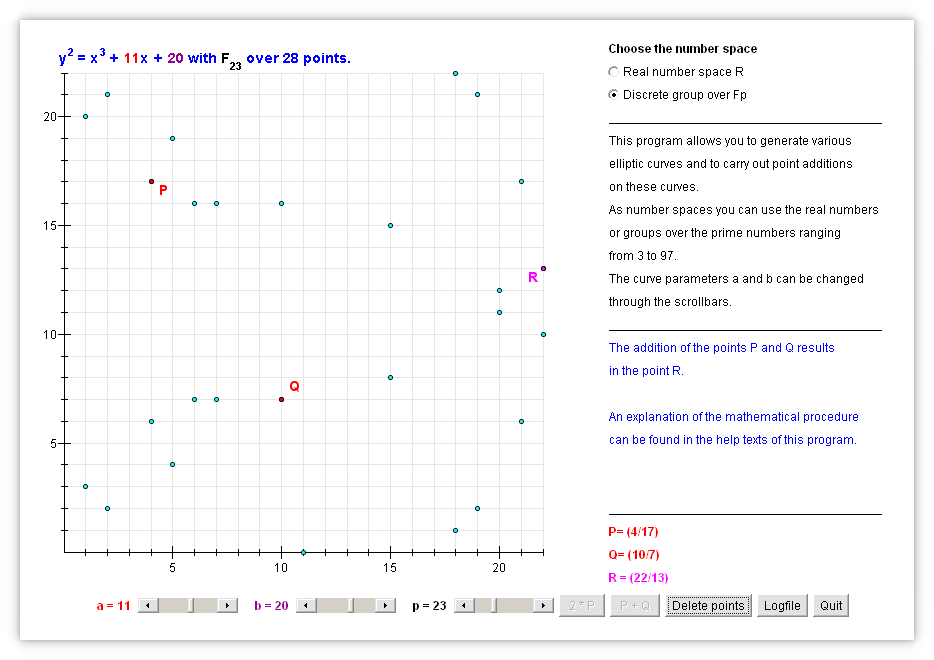
The addition leads to scaling by iterated addition. That is,
As the group of points on a finite field is finite (of cardinality approximately ), necessarily for any point the set is finite. That is, there is and in such that , that is, there is a whole such that .
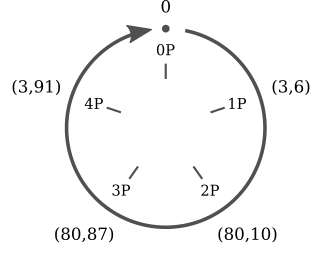
Grau (2018a) shows for an elliptic curve over a finite field the addition table between the points, and for each point the finite cyclic group generated by it. The cardinality is the smallest such that and is called the order of the point .
Elliptic Curve Cryptography uses Diffie-Hellman Key Exchange to
Encryption by the ECC is standardized by the
ECIES (Elliptic Curve Integrated Encryption Scheme), a
hybrid procedure (asymmetric cryptography with symmetric
cryptography).
Once the mutually secret
key (= a point on the finite elliptic curve) is agreed on, Alice and Bob
derive from it a key to a symmetric cipher like AES or
3DES . The derivation function that transforms a secret
information into the appropriate format is called a Key Derivation
Function, KDF. Such a standardized function is
ANSI-X9.63-KDF with the SHA-1 option. For
example, the TLS protocol
Let us transfer the Diffie-Hellman protocol from multiplication in a finite field to addition on a finite elliptic curve: Denote a point on the curve, and the -fold iterated addition over the finite elliptic curve (instead of and for a finite field).
one chooses first
To resist
Then one chooses
The critical cryptographic number is the order of the base point that should be big enough.
To resist
To find a base point whose order is big enough, proceed as follows:
That the point thus found has order can be shown by Langrange’s Theorem which asserts that where
For example, is a group and a subgroup.
Demonstration: For every point we have by Lagrange’s Theorem. That is, for , and for the Lagrange Theorem divides . Since is prime, either , or . Since , or , so .
Example (of a base point).
The elliptic curve Curve25519 with
over
with
where
, uses as base point
uniquely determined by
In the ECDH (Elliptic Curve Diffie-Hellman) protocol,
for Alice and Bob to overtly build a secret key, they first combine
and then
We note that for both to compute the same key , the addition must satisfy the associative and commutative law; that is, it is indispensable that be a group.
The ECDHE protocol, where the additional final
E stands for ‘Ephemeral’, is, regarding the key exchange,
the same as the ECDH protocol, but discards the keys (which
are necessarily signed by permanent keys to testify the identity) after
the session. Corbellini (2015b) is an implementation in
Python of ECDH.
How much older is RSA compared to ECC?
Around 20 years.
How does the ECC Diffie-Hellman key exchange compare
to the original Diffie-Hellman key exchange? The ECC
Diffie-Hellman key exchange uses points on an elliptic curve given by
pairs of numbers whereas the original Diffie-Hellman key exchange uses
simple numbers.
How do the key sizes between RSA and
ECC compare? Usual are 2048 bits for
RSA and 224 bits for
ECC.
How much faster is ECC compared to
RSA?
Asymmetric cryptography relies on a trapdoor function, which
RSA ), butRSA ) must be practically incomputable without
knowledge of a shortcut, the key!This difficulty of calculating the inverse corresponds to the difficulty of decryption, that is, inverting the encryption. To complicate the computation of the inverse function (besides facilitating the computation of the proper function) is done using modular (or circular) arithmetic*, that we already from the arithmetic of the clock, where is considered equal to .
Let us denote .
The most current cryptography widely in use uses elliptic curves (given by an equation ) where one can add points on them: if a line passes for and . By restricting the solutions to points in for a large prime number and fixing a point on the curve,
while it is easy to compute the exponential, that is, for , compute
in contrast, given a point
, it is difficult to compute the logarithm: that is,
how many times
has been added, the number
such that
. By virtue of this point addition, the Diffie-Hellman
protocol (over
)
has an analog over Elliptic Curves.
Instead of multiplying repeatedly ( times) the base in , that is, computing
add repeatedly ( times) a point , that is, compute
The advantage of using elliptic curves are shorter key sizes: Because, depending on the number of bits of the used modulus , regarding the fastest presently known algorithms:
For example, the security of a 2048 bit key for the
multiplicative logarithm equals approximately that of a 224
bit key for the logarithm over an elliptic curve. To a length of
512 bits of a key for an elliptic curve, corresponds a
length of 15360 bits of an RSA key.
ECC, elliptic curve cryptography, is becoming the new
standard because its cryptographic problem (the logarithm over a finite
elliptic curve) is currently computationally more difficult than that of
RSA (the factoring in prime numbers) or DH
(the logarithm over the multiplicative group of a finite field). small
keys for the ECC achieve the same level of security as
large keys for the RSA or DH. As an example,
the security of a 224 bits key from the ECC
corresponds to that of a 2048 bits key from the
RSA or DH. This factor in reducing key sizes
corresponds to a similar factor in reducing computational costs.
Regarding usability,
ECC public key can be shared by spelling it out (it
has 56 letters in hexadecimal notation,RSA or DH has to be
shared in a file (which is for convenience referred to by a
fingerprint).What key size in ECC is as secure as a
bit key in AES ?
What key size in ECC is as secure as a 256 bit key
in AES?
What certificate size in ECC is as secure as a 256
bit key in AES?
Use Grau (2018d) to get an intuition for the graphs over finite domains.
Read Chapter 12 on elliptic curves of Aumasson (2017).
Use CrypTool 1 to observe the addition of points on an
elliptic curve.
See the book Sweigart (2013a) for implementing some simpler
(asymmetric) algorithms in Python, a readable
beginner-friendly programming language.
Read the parts of the book Schneier (2007) on understanding and implementing modern asymmetric cryptographic algorithms.
On completion of this chapter, you will have learned …
… How a user can be authenticated by:
… How authentication is most securely achieved over distance.
… How the secret is never revealed by challenge and response protocols.
… How no information other than the knowledge of the secret is leaked by zero-knowledge proofs.
… How Kerberos mediates between users and servers without either one revealing her password to the other.
Authentication is the identification of a person or of data; the confirmation
This chapter treats exclusively the former type, the identification of a person, the user; particularly important on the Internet where the person is far away. In this sense identification is telling a computer or a network who the user is, usually by her user (or account) name. This is followed by authentication, the verification of the identity of a user, that is, convincing a computer that a person is who he or she claims to be.
To authenticate, the user can use as a proof information that
only she knows, such as a password or personal identification number (PIN),
only she has, such as
only she is described by (what she is) such as biometric identifiers (recognition of facial features, fingerprint, …).
Authentication should not be confused with authorization, the final confirmation of authentication that determines the user’s eligibility to access certain contents, that is, what a user is allowed to do or see.
The authentication protocol can be simple or two-factor, that is:
and one-way or mutual, that is,
A, such as the user, authenticates
herself to party B, andB, such as the server,
authenticates himself to party A.Most operating systems (such as Linux) and applications store a hash of the authentication data rather than the authentication data itself. During authentication, it is verified whether the hash of the authentication data entered matches the hash stored. Even if the hashes are known to an intruder, it is practically impossible to determine an authentication data that matches a given hash.
A password is a secret sequence of letters attached to a user identity that grants access to a system (such as a computer) after deriving it from the data of authorized users stored on the system.
password: a secret sequence of letters attached to a user identity that grants access to a system (such as a computer).
It is the most common approach for authentication: gratis, convenient and private. It should be easy to memorize but difficult to guess.
Comparing authentication by what one knows (such as a password) to
what one is (biometric data such as a fingerprint), the advantages are:
what one has (such as a smart-card), the advantages are:
The user’s limitation in memorizing sequences of symbols. The more meaningful, the more easily guessed (for example, a word of the user’s tongue), but the more patternless, the harder to remember. A compromise is a passphrase, that is, a complete sentence instead of a single word; though longer, its content is more meaningful and thus more easily remembered than a patternless sequence of symbols. To shorten it, the first letter of each word is taken. For example, “Better to light one candle than to curse the darkness.” can become “B2l1ct2ctd.”.
Another workaround is a password manager, a program that stores all passwords in a file encrypted by a master password.
However,
Can be acquired over distance; as a workaround, two-factor authentication requires a second ingredient to authenticate, which usually has to be spatially close to the user, such as a hardware token.
Attacks during the entry of another person’s password are:
spying during the entry of the password. Workarounds are inconvenient, for example,
keylogging
login spoofing where one user’s account a login entry form is faked so that the next user’s entered login data, instead of granting access, are stored, display an error message and log the first user out.
asking a user for the password, either through e-mail or on the phone as a purported system administrator.
asking a system administrator for the password by posing as a purported user who has forgotten her password;
asking a user to change her password on a purported entry form.
Attacks on another person’s stored password exploit principally the following deficiency: Since passwords have to be memorized, they tend to be memorizable, that is, follow patterns. For example, are built from (birth)dates, counts and words, in particular names. Common are (reversing, capitalizing, … ):
These more likely candidates can then be guessed first. Or, instead of building likely passwords, the attacker uses those already leaked to begin with.
A challenge-response protocol poses a task that can be solved only by a user with additional authentication data; usually:
challenge-response protocol: poses a task that can be solved only by a user who has the authentication data.
A Zero-knowledge Protocol goes, in theory, further, as it shows how a claimant can prove knowledge of a secret to a verifier such that no other information (than this proof of knowledge) is disclosed; however:
Zero-Knowledge Protocol: a protocol (first presented in Goldwasser, Micali, and Rackoff (1989)) to prove knowledge of a secret but disclose no other information.
A challenge-response protocol poses a task that can be solved only by a user with additional authentication data. For example,
thus proving that the user could decrypt the original value. For example, smart-cards commonly use such a protocol. Such a (randomly) generated value is a nonce (number used once) and avoids a replay attack where the exchanged data is recorded and sent again later on.
nonce: stands for (a randomly generated) number used once used in a cryptographic protocol (such as one for authentication).
For example, in CRAM-MD5 or DIGEST-MD5,
challenge to the
client. response = hash(challenge + secret) and
sends it to the server. response and
verifies that it coincides with the client’s response. Such encrypted or hashed information does not reveal the password itself, but may supply enough information to deduce it by a dictionary (or rainbow table) attack, that is, by probing many probable values. Therefore information that is (randomly) generated anew enters on each exchange, a salt such as the current time.
salt: a (randomly) generated number that enters additionally into the input of a hash function to make its output unique; principally if the additional input is a secret information such as a password.
Observation. Nonce, Salt and IV (Initialization Vector) are all numbers that are (usually) randomly generated, disclosed, used once in a cryptographic process to improve its security by making it unique. The name is given according to its use:
Challenge-Response protocols such as those presented below are used,
for example, in object-relational databases such as
PostgreSQL, or e-mail clients such as
Mozilla Thunderbird.
Digest-MD5 was a common challenge-response protocol that
uses the MD5 hash function and specified in
RFC2831. It is based on the HTTP Digest Authentication (as
specified in RFC2617) and was obsoleted by Melnikov (2011)
CRAM-MD5 is a challenge-response protocol based on HMAC-MD5, Hashing
for Message Authentication as specified in Krawczyk, Bellare, and Canetti (1997), that uses
the MD5 hash function. The RFC draft Zeilenga (2008) recommends obsoleting it by
SCRAM.
nonce.HMAC(secret, nonce).HMAC(secret, nonce) and checks
whether it coincides with the client’s response to be convinced that the
client knew secret.No mutual authentication, that is, the server’s identity is not verified.
The used hash function MD5 is quickly computed, and
thus facilitates dictionary attacks. Instead, key stretching, that is,
using a hash function that is deliberately computationally expensive is
preferable.
Weak password storage:
Dovecot) store an intermediate hash
value of the password: While this prevents storage of the plain
password, for authenticating with CRAM-MD5, knowledge of the hash value
is equivalent to that of the password itself.Salted Challenge-Response Authentication Mechanism
(SCRAM) is a challenge-response protocol for mutual
authentication specified in Menon-Sen et al. (2010) (that should supersede
CRAM-MD5 as proposed in Zeilenga (2008)).
While in CRAM the client password is stored as hash on
the server, now knowledge of the hash (instead of the password) suffices
to impersonate the client on further authentications: The burden has
just been shifted from protecting the password to its hash.
SCRAM prevents this by demanding additional information (on
top of the authentication information StoredKey stored on
the server) that was initially derived from the client’s password
(ClientKey). Advantages of SCRAM in comparison to older
challenge-response protocols, according to loc.cit., are:
The authentication information stored on the server is insufficient to impersonate the client. In particular,
supports mutual authentication (by the client and server).
When the client creates a password Password, the server
stores derived keys StoredKey and ServerKey
together with the parameters used for its derivation, as follows:
The client:
SaltedPassword by applying the password
hashing function PBKDF2 (which is variable; by default it
is PBKDF2, but nowadays, for example, bcrypt
is recommended) IterationCount many times on the input
given by the password Password and the salt
Salt, that is,
SaltedPassword := PBKDF2(Password, Salt, IterationCount)ClientKey respectively ServerKey
by applying the HMAC function on SaltedPassword with the
public constant strings “Client Key” respectively “Server Key”, that is,
and
StoredKey by hashing ClientKey,
that is, StoredKey := H(ClientKey) and sends
ServerKey and StoredKey to the server (but
not ClientKey). The server stores StoredKey, ServerKey,
Salt and IterationCount to later check proofs
from clients and issue proofs to clients: ClientKey is used
first to authenticate the client against the server and
ServerKey is used later by the server to authenticate
against the client.
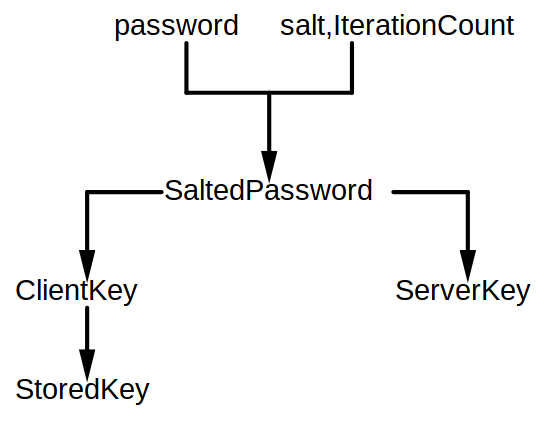
The server only stores the public part of the root (Salt and
IterationCount) and the leafs (StoredKey and
ServerKey) of this tree. That is, the password is never
sent to the server, but only:
the salt,
the iteration count,
ServerKey and StoredKey, that is,
Thus, after a database breach, that is, after an attacker has stolen
a ServerKey, a client’s password does not need to be
replaced, but only the salt and iteration count changed and
ClientKey and ServerKey replaced.
iteration count: Given an initial input, apply a hash function that many times ( ) to the output.
For the server to authenticate the client:
client-name and a client-nonce).salt, iteration
count ic and a server-nonce.Therefore, both, the client and server know
AuthMessage := client-name, client-nonce, salt, ic, server-nonce.
The client
creates proof of her knowledge of StoredKey by
computing
ClientSignature := HMAC(StoredKey, AuthMessage)
ClientProof := ClientKey XOR ClientSignatureand sends ClientProof to the server.
The server
recovers ClientKey by
computing ClientSignature (by knowing
StoredKey from storage and AuthMessage from
this exchange), and
deciphering ClientKey' from the one-time pad
ClientProof by computing
ClientKey' = ClientProof XOR ClientSignaturecomputes StoredKey' by H(ClientKey),
and
checks whether the computed StoredKey' coincides
with the stored StoredKey; if so the client is successfully
authenticated.
If just ClientSignature were sent, then an attacker who
knows StoredKey could impersonate the client. Instead,
ClientProof additionally requires the client to know
ClientKey. Therefore, the value of ClientKey'
that is calculated on the server should be immediately and irreversibly
(say, by zeroing) deleted after verification.
The client initiates the protocol by sending the Client’s First Message to the server that contains:
ClientNonce randomly generated by the
client.In response to the reception of a valid message from the client, the server sends the Server’s First Message to the client that contains:
ServerNonce randomly generated by the
server.salt randomly generated by the server that
enters with the password as input of a hash function.IterationCount
generated by the server that indicates how many times the hash function
is applied to the salt and the password to obtain its output.The concatenation of the client’s and server’s message is
AuthMessage
AuthMessage = username, ClientNonce, ServerNonce, salt, IterationCountThe client creates the proof for the server by computing:
ClientSignature = HMAC(StoredKey, AuthMessage),
andwhere StoredKey can be recomputed by
StoredKey = H(ClientKey) and
using the salt and IterationCount from
AuthMessage and the user’s password.
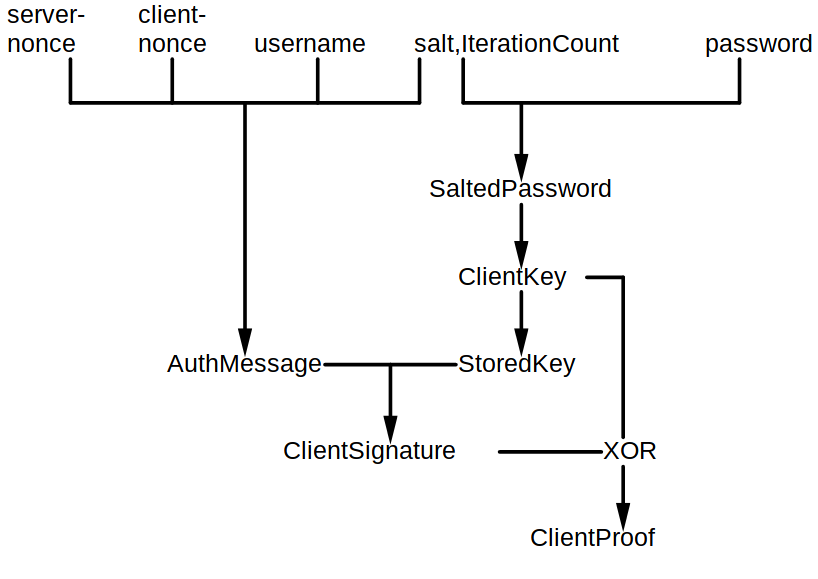
ClientNonce and
ClientProof to the serverClientProof from the client
by
recalculating
ClientSignature = HMAC(StoredKey, AuthMessage),ClientKey by
,StoredKey' = H(ClientKey'), andchecking whether .
If just ClientSignature were sent, then an attacker that
knows StoredKey could impersonate the client. Instead,
ClientProof additionally requires the client to know
ClientKey. Therefore, the value of ClientKey'
that is calculated on the server should be immediately and irreversibly
(say, by zeroing) deleted after verification.
We conclude that instead of the client’s password, sent were
ClientNonce and server nonce
ServerNonce,salt,IterationCount,The server computes
ServerSignature = HMAC(ServerKey, AuthMessage)
The server sends ServerSignature
The client checks ServerSignature from the server
by
recalculating
checking whether .
We conclude that instead of the server’s key, sent was
ServerSignature = HMAC(ServerKey, AuthMessage).If an attacker knows
StoredKey from the server, andAuthMessage and ClientProof from an
authentication exchange,then he can calculate ClientSignature, thus
ClientKey and can impersonate the client to the server.
A Zero-Knowledge Protocol shows how a claimant can prove knowledge of a secret to a verifier such that no other information is disclosed; that is, not a single bit of information, other than the validity of the claimant’s claim, is disclosed (to anyone, including the verifier).
Proof is meant probabilistically, that is, the claim is true beyond any reasonable doubt. More so, because the proofs are independent of each other, the probability can be increased as much as desired by increasing their number. The impossibility to gather information on the secret from that exchanged relies on the computational difficulty to solve a mathematical problem.
That no information whatsoever is leaked cites the following benefits:
While claiming to know the secret alone is unconvincing, the leakage
of information during classical protocols in which a claimant
C proves knowledge of a secret to verifier V,
still compromises the secret as follows:
C transmits his password to V, then
V and everyone who eavesdropped this transmission obtains
all data to impersonate C from this moment on.V and an
eavesdropper can during every occurrence accumulate new information on
the secret so that it eventually yields to it. For example, if the
challenge is the encryption of a plaintext, and the attacker can choose
this plaintext, then this is a chosen-plaintext attack.To weigh up the advantages and inconveniences between a zero-knowledge proof and a digital signature by a private key (verified by its corresponding public key):
The security of both, most zero-knowledge protocols and public-key protocols, depends on the unproved assumption that cryptanalysis is computationally as difficult as a mathematical problem (such as the computation of quadratic residuosity, the decomposition of an integer into its prime factors, discrete logarithm, …).
The concept of
An interactive protocol is turned into a non-interactive one by taking the hash of the initial statement and then send the transcript to the verifier (who also checks that the hash was computed correctly).
Practical protocols were introduced in Fiat and Shamir (1987) and Feige, Fiat, and Shamir (1988).
The latter introduced so-called sigma protocols in three steps:
IEEE 1363.2 defines zero-knowledge password proof as “an interactive zero-knowledge proof of knowledge of password-derived data shared between a prover and the corresponding verifier”.
Ali Baba’s cave illustrates the principles behind a zero-knowledge
proof: In a circular cave there is a door invisible from the entrance
that bars any passage if not opened by a password (such as “Sesame”).
For C to prove to V that he knows the password
without disclosing it:
C enters the cave unobserved from V till
standing in front of the door’s left or right.V demands C to return to the entrance
coming from the left or right.Because the probability that C entered the cave on the
same side as V asked for to leave on is one half and all
proofs are independent, for example, after
proofs the chance C does not know the password is
,
less than a thousandth.
While V is convinced that C knows the
password, she cannot convince anybody else. Even if V
recorded the sequence, then it could have been mutually fixed in
advance.
Schnorr (1991) presented a zero-knowledge protocol simple enough to run on smart cards. Knowledge of discrete logarithms is proved, that is,
P knows an integer
, andV knows
where
is a prime number. For P to prove knowledge of
without revealing it:
P chooses some integer
and sends
to V .
V tosses a coin and sends the result
in
to P .
P sends to V
This is a zero-knowledge protocol, because
If
, then no knowledge of
is needed. If
however, then V can verify whether P knows
by
where both values on the right-hand side are known. Since the
probability that
is
and all proofs are independent, after, say,
proofs the chance V does not know
is
.
The security of the Fiege-Fiat-Shamir protocol rests on the assumed
computational difficulty of extracting square roots modulo large
composite integers whose prime factors are unknown (similar to
RSA):
1024
bits.P, as follows:
P, the prover,
V .V, the verifier,
P .P, the prover,
V, the verifier,
P knows
.P knows
.If
, then no knowledge of the private key
is needed. If
however, then V can verify whether P can
compute
,
thus presumably knows
. Because the probability that
is one half and all proofs are independent, for example, after
proofs the chance V does not know
is
,
less than a thousandth.
This is nearly a zero-knowledge protocol, however, care must be taken:
V could gather information by
manipulating the “random” bits.CRAM a hash of the client password is stored
as is on the server, while in SCRAM additional data (salt)
enters. Biometric authentication identifies the user of a computer by
either physical human characteristic, such as:
or behavioral human characteristic, such as:
typing characteristics such as the speed of keystrokes or the occurrence of typos (particularly useful to supplement a log-in dialogue);
handwriting characteristics; either static where an image is used, or dynamic where the traces on a tablet are evaluated by the functions (of time):
voice properties (speaker recognition; particularly useful to verify the identity of telephone customers). Each spoken word is decomposed into its formants, the dominant frequencies, and then physiological and behavioral characteristics identified:
Comparing authentication by what one is (for example, a fingerprint) to
what one knows (for example, a password), the advantages are:
what one has (for example, a token), the advantages are:
For example, the German Chaos Computer Club (CCC) and its collaborators have demonstrated time and again the ease of forging fingerprints, for example, using wood glue and sprayable graphene. The many successful forgery attacks against biometric identification, such as fingerprints and photo ID, leads to the conclusion to treat them, instead of a replacement for passwords or smart-cards, rather
List advantages of authentication by what one knows over what one is:
In a (distributed) system, only if
then the secret itself for authentication could be responsibly sent in the clear. Otherwise, to ensure that the secret for authentication is seen by none other than possibly the intended recipient, the secret itself must never be sent in the clear. Instead, both the user and the system convince each other they know the shared secret (usually a password). That is, the identification data itself is never sent, but only proof she has access to it beyond any doubt. In practice, for a system that is password-based, the most popular approach are challenge-response systems. A challenge-response protocol poses a task that can be solved only by a user with additional authentication data: Usually,
challenge-response protocol: poses a task that can be solved only by a user who has the authentication data.
As best practice, even though the secret itself is never sent, it is still advisable to encrypt all communication to establish authentication, for example, by public-key encryption.
Other approaches are:
TANs (TransAction Numbers) in banking.
However, if the identification data can be eavesdropped and its use for
authentication, and thus invalidation, be prevented (for example, by
logging into a forged copy of the bank’s Website), then it can be used
later. single-use system: the identification data is only used once.
second-channel system: the identification data is sent via a second channel.
The FIDO (Fast IDentity Online) Alliance was officially founded in
February 2013 to develop open and license-free industry standards for
authentication on the Internet in arrangement with many companies such
as Google or Microsoft. On December 9, 2014,
the first standard FIDO v1.0 was released that specifies:
These standards aim to facilitate authentication on the Internet by using a user’s
instead of
That is, no longer needs a user to memorize numerous secure passwords (though at the cost of the drawbacks discussed in Section 11.1). In comparison with previous methods of two-factor authentication such as SMS verification codes, FIDO2 requires the key, such as the smart phone, to be physically near your computer. FIDO2 (“Moving the World Beyond Passwords”) consists of the
Personal data and private keys are always and exclusively in the hands of the user and are not stored on public servers. To register via FIDO2 an account on a server:
This way, the FIDO2-key can identify itself with an individual key at each server without the server obtaining information on the key pairs for the same FIDO2-key on other servers. That is, the FIDO2-key generates a separate key pair for each service, based on the domain of the other party. For example, Ebay and Google, cannot determine which of their users use the same FIDO2-key. In practice, this is an advantage (on the server-side!) to authentication by a password where a user often uses similar passwords on different servers.
A FIDO2 key (or authenticator or token) is the device by which to authenticate oneself to a service. It can be
either an external device to connect to the user’s PC or smart phone via USB, NFC or Bluetooth; such as
NFC token (Near Field Communication; a wireless
communication technology to exchange data between closely located
devices, that is, about a decimeter apart; jointly developed by Sony and
Philips and approved an ISO standard in December 2003),or an internal authenticator. That is, software that uses the crypto chip of your PC, smart phone or tablet for FIDO2, supported by Windows 10 and Android 7 and above.
Against misuse of the FIDO2 key, it can be additionally secured biometrically or with a password/PIN. If the stick is lost, then either a registered backup key is available or one has to identify oneself again by, say, the mobile phone number in combination with an e-mail address or alike.
A FIDO2 key can either be used instead of a password or in addition to it, as a second factor. Depending on how a service has implemented FIDO2, the key suffices for logging in (one-factor authentication) or additionally entering a password (two-factor authentication) is necessary. FIDO2 one-factor authentication already is available for Microsoft.com, Outlook.com, Office 365 and OneDrive in the Edge browser. FIDO2 two-factor authentication works, for example, with Google, GitHub, Dropbox and Twitter.
One solution to the problem of key distribution, that is,
is a central authority who is
so that each correspondent has only to protect one key, while the responsibility to protect all the keys among the correspondents is shifted to the central authority.
Kerberos (pronounced “kur-ber-uhs”) is named after Cerberus, the three-headed watchdog at the gate to Hades; while Cerberus authenticates dead souls, Kerberos mutually authenticates users over a network:
Kerberos is a network protocol (as specified in RFC 1510 — The Kerberos Network Authentication Service V5) which permits users to securely authenticate to each other over an insecure network by a trusted third party, the Key Distribution Center (KDC) . Once a user is authenticated (Kerberos), she is authorized by access protocols such as LDAP (Lightweight Directory Access Protocol).
Kerberos: a network protocol to securely authenticate clients to servers over an insecure network by a trusted third party.
Key Distribution Center (KDC): stores the symmetrical keys of all registered users and servers to securely authenticate them.
The Key Distribution Center (KDC) stores the symmetrical keys of all registered users (be it client or server) to authenticate them as an intermediary third-party. Due to its critical role, it is good practice to have a secondary KDC as a fallback.
Kerberos groups users into clients and (service) servers (SSs) that host services for the clients. The authentication protocol authenticates a client only once so that she is trusted by all SSs for the rest of her session. This is achieved by
The ticket, to further obstruct man-in-the-middle attacks (in comparison to a mere key authentication),
The KDC is split up into :
an Authentication Server (AS): To authenticate each user in the network, the AS stores a symmetric key for each user, be it client or service server (SS), and which is only known to itself, the AS, and the user.
a Ticket-Granting Server (TGS):
Service Server (SS): the server that hosts a service the user wants to access.
Authentication Server (AS): stores for each user (be it client or server) in the network a symmetric key known only to itself, the AS, and the user.
Ticket-Granting Server (TGS): generates a session key as part of a ticket between two users of the network after authentication.
To allow a user (commonly referred to as client) to securely
communicate with another user (commonly referred to as Service Server or
Application Server (SS or AP), the
server that hosts a service the client wants to access) via the
KDC, the Kerberos protocol defines ten messages, among
them:
| Code | Meaning |
|---|---|
KRB_AS_REQ |
Kerberos Authentication Service Request |
KRB_AS_REP |
Kerberos Authentication Service Reply |
KRB_TGS_REQ |
Kerberos Ticket-Granting Service Request |
KRB_TGS_REP |
Kerberos Ticket-Granting Service Reply |
KRB_AP_REQ |
Kerberos Application Request |
KRB_AP_REP |
Kerberos Application Reply |
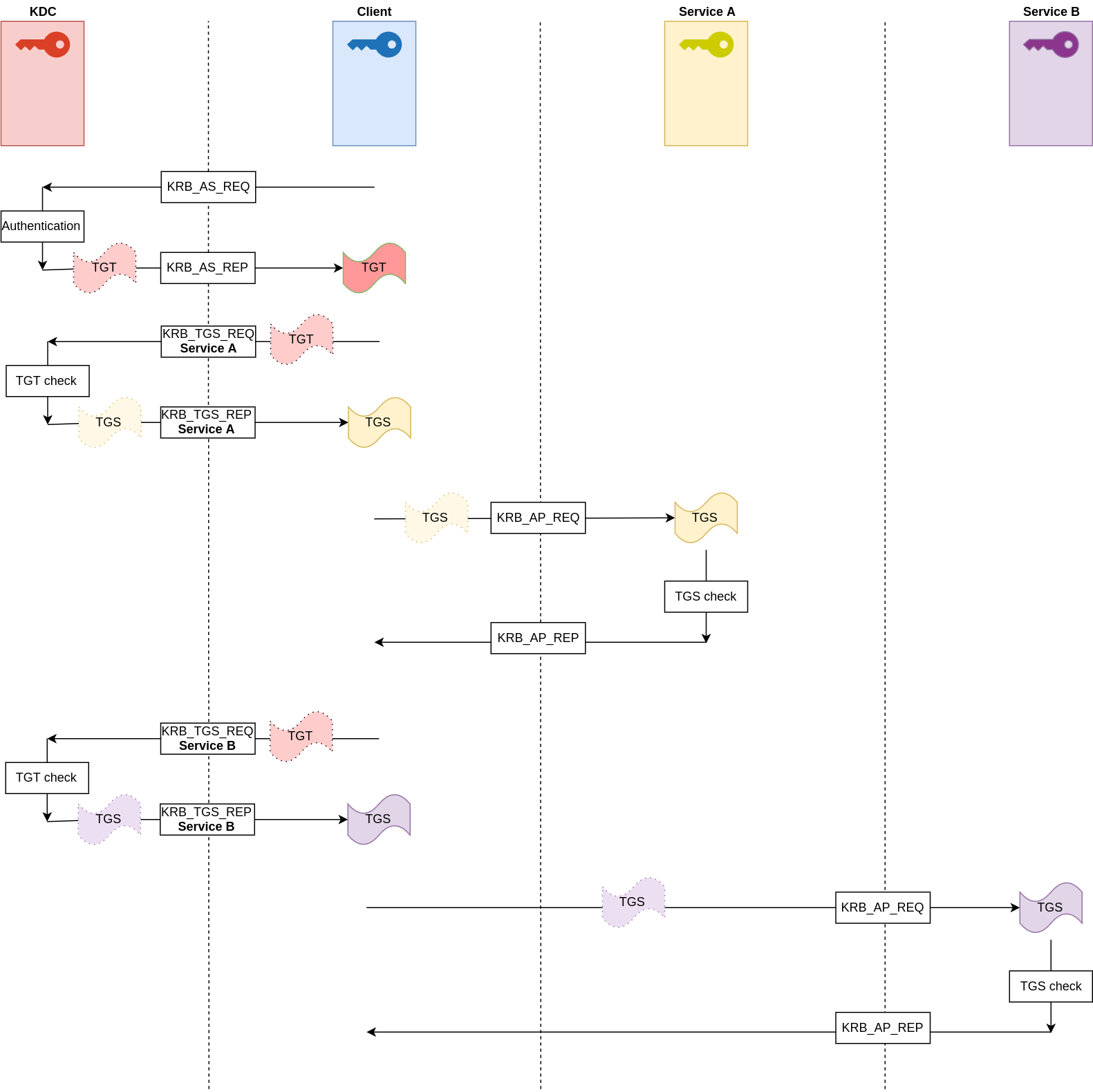
The client, to authenticate to the AS,
KRB_AS_REQ) using a long-term shared secret (client’s
key), andKRB_AS_REP).The client, to authenticate to the SS via the AS,
AS using her TGT, andKRB_TGS_REQ) a ticket from the
TGS (KRB_TGS_REP) that contains a session key
between the client and the SS.The TGS, to create the ticket,
The client, to authenticate directly to the SS:
decrypts the client-to-server session key using her own key, and
sends to the SS (KRB_AP_REQ and
KRB_AP_REP)
The SS
The client decrypts, using the client-to-server session key, the incremented timestamp and checks it. If the check succeeds, then the client can trust the server and can start issuing service requests to the server.
The server provides the requested services to the client.
The Kerberos protocol is based on the Needham-Schroeder authentication protocol, invented by Roger Needham and Michael Schroeder in 1978, and designed to securely establish a session key between two parties on an insecure network (the Internet, for example) by a symmetric-key algorithm.
MIT developed Kerberos to protect network services provided by Project Athena that aimed at establishing a computing environment with up 10,000 workstations on varying hardware, but where a user could on every workstation access all files or applications in the same user interface; similar to what a browser achieved today. Versions 1, 2 and 3 were only used at MIT itself. Version 4 employed the Data Encryption Standard encryption algorithm, which uses 56-bit keys, and was published in 1989.
In 2005, the Internet Engineering Task Force Kerberos working group introduced a new updated specifications for Kerberos Version 5, and in 2007, MIT formed the http://www.kerberos.org for continuation of development.
MIT Kerberos is the reference implementation that supports Unix, Linux, Solaris, Windows and macOS, but other commercial and non-commercial implementations exist: Most notably, Microsoft added a slightly altered version of Kerberos V5 authentication in Windows 2000.
Kerberos originally used the DES algorithm for
encryption and the CRC-32, MD4, MD5 algorithms for hashing, but nowadays
Kerberos implementations can use any algorithm for encryption and
hashing.
/tmp directory and only deleted after their expiration,
thus, in multi-user system, risk to be stolen.5 minutes difference and preferably achieved by the Network
Time Protocol; NTP) of the involved parties because of the period of
validityLet us detail each step from logon and authentication to service authorization and request

The client sends a cleartext message to the
Authentication Server (AS) asking for services on
behalf of the user (KRB_AS_REQ).
The AS checks whether the client is in his database.
If she is, then the AS sends back the following two messages to the client:
Client/Ticket-Granting Server (TGS) Session Key, encrypted using the secret key of the client.
Ticket-granting Ticket (TGT), encrypted using the secret key of the TGS, and which includes the
Once the client receives messages A and
B, she retrieves the Client/TGS Session Key by
decrypting message A using her secret key.
The Client/TGS Session Key is used for further communication with TGS. At this point, the client has enough information to authenticate herself to the TGS.
We observe that neither the user nor any eavesdropper on the network
can decrypt message B, since they do not know the TGS’s
secret key used for encryption.
To request services, the client sends the following two messages
C and D to the TGS:
Composed of the
ID) of the requested
service.Authenticator, encrypted using the Client/TGS Session Key, and which is composed of the
Once the TGS receives messages C and D, he retrieves the Client/TGS Session Key by
The TGS
retrieves the client ID and its timestamp by decrypting message
D (Authenticator) using the Client/TGS Session Key,
and
sends the following two messages E and
F to the client:
Client/Server Session Key, encrypted using the Client/TGS Session Key.
Client-to-Server ticket, encrypted using the Service Server ’s (SS) secret key, which includes the
At this point, after the client receives messages E and
F from the TGS, the client has enough information to
authenticate herself to the SS.
The client connects to the SS and sends the following two
messages F and G:
f. from the previous step (the Client-to-Server ticket, encrypted using the SS's secret key).
g. a new Authenticator, encrypted using the Client/Server Session Key, and which includes the
- client ID, and
- timestamp.The SS
retrieves the Client/Server Session Key by decrypting the ticket using his own secret key,
retrieves the Authenticator by decrypting it using the session key, and
authenticates to the client by sending the following message
H to the client :
The client checks whether the timestamp is correctly updated by
decrypting Message H using the Client/Server Session Key.
If so, then the client can trust the server and can start issuing
service requests to the server.
The server provides the requested services to the client.
A smart card has the form of a credit card, but contains a microprocessor to securely store and process information. (In contrast, a magnetic-stripe card only stores little information (around bytes) but cannot process it.) Security algorithms are implemented on the card so that only properly authorized parties can access and change this data after they have authenticated themselves.
The first smart card was invented in 1973. While it initally consisted only of read and write memory, a microprocessor was added in 1976. In 1981, the French state telephone company introduced it to store a pre-paid credit, which was reduced when calls were made. As memory capacity, computing power, and data encryption capabilities of the microprocessor increased, smart cards are graudally replacing cash, credit or debit cards, health records, and keys.
Most of the processing in smart cards is dedicated to cryptographic operations; in particular, encryption between on-chip components To function, a smart card needs external power and clock signal provided through contact with a smart card reader (that usually can write as well). The operating system on most smart cards implements a standard set of control commands such as those standardized in ISO 7816 or CEN 726.
There is a single Input/Output port controlled by small data packets called APDUs (Application Protocol Data Units). Because data flows only at around 9600 bits per second and half-duplex, that is, the data can either flow from the reader to the card or from the card to the reader, but not simultaneously in both directions, the smart card can only be read out slowly, thus complicating attacks. The reader sends a command to the smart card, the card executes the command and returns the result (if any) to the reader; then waits for the next command. The smart card and the reader authenticate each other by a challenge-response protocol using a symmetric key encryption:
(and possibly with interchanged roles). Once mutually authenticated, each exchanged message is verified by a message authentication code (HMAC) which is calculated using as input the message, encryption key, and a random number.
For example, the UICC (Universal Integrated Circuit Card) or Universal Subscriber-Identity Module (USIM) is a smart card used in mobile phones in GSM and UMTS networks. It ensures the integrity and security of all kinds of personal data, and it typically holds a few hundred kilobytes. The Subscriber Identification Modules (SIM) is an application in the UICC that stores the subscriber’s information to authenticate her with the network:
Comparing authentication by what one has (for example, a smart card) to
what one knows (for example, a password), the advantages are:
to what one is (for example, the fingerprint), the advantages are:
less sophisticated and expensive hardware (such as an iris scanner), and
cryptographic keys are stored securely on a device; thus avoids forgeries with fingerprints or vein scanners; In particular, storing keys on a smartcard, that is accessed by a USB reader with its own keyboard, instead of a digital file has the advantage that reading the keys from a smart card:
List advantages of authentication by what one knows over what one has:
List disadvantages of authentication by what one knows over what one has or is:
Anonymity comes from the Greek word anonymía, “name-less”, and means “namelessness”. Colloquially, it means that a person’s identity is unknown. More abstractly, that an element (for example, a person or a computer) within a set (for example, a group or network) is unidentifiable (within this set).
Protecting one’s identity from being disclosed is not only necessary for someone who acts against the law, for example, when attempting to exploit a computer in a network, but also as a precaution to a possible abuse; for example, to amass data of the user’s online habits to build a profile for targeted advertising.
Countermeasures are
However, these countermeasures involve inconveniences, such as an
involved setup and slower data transfer. As a less compromising
practical measure is to adapt best practices for protecting one’s
privacy on the world wide web, for example, by using the
Firefox browser with add-ons that filter out
such as
uBlock Origin,Privacy BadgerDon't track me Google, andDecentraleyes.Also, there is a need for anonymised datasets, for example:
for hospitals to release patient information for medical research but withhold personal information.
to verify whether a password has leaked, for example, by the
I Been Pwned web form by Troy Hunt that contains over half
a billion leaked passwords. This prevents Credential Stuffing where
usernames and passwords from compromised websites are entered into
website forms until compromised user accounts are found; an attack
likely to succeed, because
For example, the I Been Pwned web form transmits only
the first five digits of the SHA-1 of the password to
compare, thus leaking little personal information. This achieves what is
generally called k-Anonymity where a data set has for each
record
identical copies.
Identity, from Late Latin identitas, from Latin idem, same, and entitas, entity, are the characteristics by which someone or something is uniquely recognizable, that is, held by no other person or thing. Identity theft is the assumption of another person’s identity, usually another person’s name or other personal information such as her PINs, social security numbers, driver’s license number or banking details, to commit fraud, for example, to open a fraudulent bank or credit card account to receive loans. With the advent of digitalized records and (the anonymity on) the Internet, identity theft has become more and more common.
For example, in SIM-card swapping, the attacker obtains a victim’s mobile-phone number to assume, temporarily, her online identity. The attacker initially obtains personal data about the victim, usually her name, mobile phone number and postal address. He then exploits that mobile operators usually offer their customers a new SIM card, for example, after the phone is lost, onto which the previous phone number is transferred. The attacker now pretends to be the actual customer to the mobile phone operator, for example, by phone in the customer service center (where often the date of birth and postal address suffice to identify oneself if no customer password was agreed on signing the contract). For example, it suffices to know the mobile phone number to reset the password of an Instagram account.
Identification is telling a computer who the user is, usually by her user (or account) name. This is followed by authentication, the verification of the user’s identity, that is, convincing a computer that a person is who he or she claims to be. To authenticate, the user prove her identity by information that
Each method with its proper advantages and disadvantages. In particular, passwords, the most common method, have to be memorizable, which in practice weakens them. The FIDO2 standard aims at replacing (or at least complementing) them by hardware and biometric authentication.
Instead of revealing the secret itself when authenticating, it is safer to prove only its knowledge. In a challenge-response authentication protocol, the successful response to the challenge requires its knowledge (such as encryption and decryption of random data by the secret key). In a zero-knowledge protocol, in contrast to a challenge-response protocol, no information whatsoever can be won on the secret key provided the computation of a mathematical function is assumed infeasible.
The Kerberos protocol mediates between users and servers by a central server that stores symmetric keys of all parties; then instead of the parties mutually proving the knowledge of their symmetric keys, it creates for each correspondence a session key of limited validity.
Read Bentz (2019) to get an idea how Kerberos works and Quisquater et al. (1989) for zero-knowledge proofs.
Read Schnorr (1991) to understand a basic zero-knowledge protocol.
Have a look at Menon-Sen et al. (2010) to get acquainted with the format of Request for Comments, in particular, thoroughly understand the SCRAM protocol.
On completion of this chapter, you will have learned …
Let us recall that the prefix Crypto-, comes from Greek kryptós, “hidden” and analysis from the Greek analýein, “to untie”: the breaking of ciphers, that is, recovering or forging enciphered information without knowledge of the key.
Cryptanalysis: Recovering or forging enciphered information without knowledge of the key.
History delivers plenty cryptanalytic success-stories; for example, among many others, the decryption of the German rotor machine Enigma by the Polish and British forces.
During World War I:
ADFGVX cipher used by the
German forces within a month just before the German army entered in
Paris in 1918 (however, still too late to save much).During World War II:
Polish and British cryptanalysis of
The U.S. Army’s Signal Intelligence Service’s (SIS) cryptanalysis of the Japanese rotor machines . The pivotal Battle of Midway for the naval war in the Pacific was won by awareness of the Japanese attack on the Aleutian Islands being a diversionary maneuver and the Japanese order of attack on Midway.
In World War II the Battle of Midway, which marked the turning point of the naval war in the Pacific, was won by the United States largely because cryptanalysis had provided Admiral Chester W. Nimitz with information about the Japanese diversionary attack on the Aleutian Islands and about the Japanese order of attack on Midway.
During a debate over the Falkland Islands War of 1982, a member of Parliament, in a now-famous gaffe, revealed that the British were reading Argentine diplomatic ciphers with as much ease as Argentine code clerks.
Cryptanalytic feats were achieved also by the defeated powers, but no success-stories to be told.
While we will present some established principles of cryptanalysis, in practice the cryptanalyst’s intuition and ability to recognize subtle patterns in the ciphertext were paramount, but difficult to convey. Today, however, cryptanalysis is based on mathematics and put into practice by efficient use of extensive computing power.
Cryptanalysis of single-key ciphers relies on patterns in the
plaintext carrying over to the ciphertext. For example, in a
monoalphabetic substitution cipher (that is, each alphabetic letter
a, b, … in the plaintext is replaced,
independently of its position, by another alphabetic letter), the
frequencies of the occurrences of the letters in the plaintext alphabet
are the same as those in the ciphertext alphabet. This can be put to
good cryptanalytic use by
A substitution by any permutation of the letters of the alphabet, such as,
| A | B | … | Y | Z |
| ↓ | ↓ | … | ↓ | ↓ |
| E | Z | … | G | A |
has keys, so a brute-force attack is computationally infeasible. But it violates the goals of diffusion and confusion: If the key (that is, the given permutation of the alphabet) exchanges the letter for the letter , then there’s
In fact, the algorithm allows statistical attacks on the frequency of
in English For example,
e,th, andthe.Thus substituting
e),th), …the), …is a good starting point to decipher the text: The more ciphertext, the more likely that this substitution coincides with that the text was enciphered by.
For example, using these frequencies on the ciphertext
ACB ACBGA ACSBDQTgives
THE THE** TH*E***for yet to be deciphered letters marked by *. By the
restrictions of English vocabulary and sentence structure, yielding
THE THEFT THREAPSAs an exercise, Dear reader, build a short English sentence with common letter frequencies, ask a friend to encrypt it and try your hands at cryptanalyzing it!
Homophones: Multiple cipher symbols for the same plaintext letter.
To hide the frequencies of the alphabetic letters, one approach is to
use homophones, a number of ciphertext symbols for the same
alphabetic plaintext letter, chosen in proportion to the frequency of
the letter in the plaintext; for example, twice as many symbols for
E as for S and so forth, so that each cipher
symbol occurs on average equally often in the ciphertext. However, other
frequencies in the plaintext (partially) still resist encryption (and
ease cryptanalysis), such as digraphs: TH occurs most
often, about 20 times as frequently as HT, and
so forth.
In practice the security of a cipher relies foremost
In contrast to single-key cryptography whose cryptanalysis exploits statistical patterns, by its reliance on computationally difficult mathematical problems (that is, whose runtime grows exponentially in the bit-length of the input), the cryptanalysis of two-key cryptography is that of computational mathematics: to find an algorithm that quickly computes the solutions of the difficult mathematical problem. Ideally, one whose runtime is polynomial in the number of input bits. However, in practice, for example, for
RSA oralgorithms whose runtime grows slower than exponentially in the number of input bits (sub-exponential) are known, but none with polynomial runtime.
ECC, elliptic curve cryptography, is becoming the new
standard because its cryptographic problem (the logarithm over a finite
elliptic curve) is (from what we know) computationally more difficult
than that of RSA (the factoring in prime numbers) or
DH (the logarithm over the multiplicative group of a finite
field). Therefore, small keys for the ECC achieve the same
level of security as large keys for the RSA or
DH. As an example, the security of a 224 bits
key from the ECC corresponds to that of a 2048
bits key from the RSA or DH. This factor in
reducing key sizes corresponds to a similar factor in reducing
computational costs. Regarding usability,
ECC public key can be shared by spelling it out (it
has 56 letters in hexadecimal notation,RSA or DH has to be
shared in a file (which is for convenience referred to by a
fingerprint).Let us compare the cryptographic problem behind ECC to
that of RSA and DH:
Both groups, the multiplicative group of a finite field and the group of a finite elliptic curve, are finite cyclic groups, that is, generated by an element of finite order . Mathematically speaking, they are equal to a group of type However, one way of this identification, from to , is a lot faster than the other way around:
Given a generator in , the identification of with for , the exponential is quickly computed in every commutative group : Given in , to calculate , expand in binary base for , …, in and calculates by multiplying by successively , …, . So That is, we calculate in group operations.
Example. For the group of points of an elliptic curve, in , and in we calculate successively , , . Let , , … be the indices of the binary digits … that are different from . So
Given a generator in , the computation of the reverse identification, the logarithm that is, given in , calculate in such that is usually hard: By Shoup’s theorem in Shoup (1997), every generic algorithm, that is, using only the operations of the group, takes at least operations (of the group) to calculate the logarithm.
A generic algorithm that achieves this speed (except a
factor) is the Baby Step, Giant Step (or Shanks algorithm):
Given
in
, to calculate
in
such that
:
This algorithm works, because:
Note. For elliptic curves, Pollard’s -algorithm is slightly faster.
This estimation of the operations necessary to compute the logarithm of a group, that is, which uses only the operations of the group, applies to generic algorithms. However, specific algorithms, that is, those that use group-specific properties (such as the units of a finite field or that of an elliptic curve), may use less.
For example, for the multiplicative group of a finite field, there
are indeed faster algorithms (called sub-exponential) to
calculate the prime factors of a product and the logarithm. They are
based on Index Calculus which makes use of the properties of
this specific group. For example, for the cryptographic problems of
RSA and Diffie-Hellman on the multiplicative
group of a finite field, that is,
there are indeed faster algorithms (called sub-exponential). They are based on Index Calculus which makes use of the properties of this specific group. The fastest known algorithm is the General Number Field Sieve; see A. K. Lenstra et al. (1993) for the computation of the prime factors and Gordon (1993) for that of the logarithm.
Its complexity is sub-exponential, roughly for large , the number of group operations is where and means a function over such that to .
In contrast, all known algorithms for the ECC
cryptographic problem, that is, calculating the logarithm over a finite
elliptic curve, are generic algorithms. For these generic algorithms, by
Shoup’s Theorem, the complexity
in the number of bits
of input is as small as possible. The fastest algorithm at present is
Pollard’s
-algorithm, which has a roughly exponential complexity of
where
.
World’s fastest supercomputer, IBM’s Summit (taking up 520 square meters in the Oak Ridge National Laboratory, Tennessee, USA) has around petaflops, that is, floating point operations per second. The number of flops needed to check a key depends for example, on whether the plaintext is known or not, but can be very optimistically assumed to be . Therefore, Summit can check approximately keys per second, and, a year having seconds, approximately keys a year.
To counter the increasing computing power, one prudently applies a Moore’s Law that stipulates that computing power doubles every other year. Therefore, every twenty years computing power increases by a factor . Therefore, to ensure that in, say, sixty years, a key not surely be found during a yearlong search by world’s fastest supercomputer at least key combinations have to be used.
For a key of bit length , the number of all possible keys is . If , then there are are possible key combinations. While this number is sufficient for now, the probability for the key to be found during a yearlong search by world’s fastest supercomputer being around , the projected fastest super computer in twenty years will likely find it in half a year. Instead, to be safe in 40 years, a minimal key length of is recommended.
This Table from A. Lenstra and Verheul (2001) compares the key sizes in bits to a security level comparable between
AES,Diffie-Hellman or
RSA.| Symmetric Key | Asymmetric Elliptic Key | Classic Asymmetric Key |
|---|---|---|
80 |
160 |
1024 |
112 |
224 |
2048 |
128 |
256 |
3072 |
192 |
384 |
7680 |
256 |
512 |
15360 |
The numbers in the table are estimated by the fastest known algorithm to solve the cryptographic problem: Given an input key with bits,
AES , the fastest known
algorithm is to try out all possible keys, whose complexity (= the
number of operations) is
,RSA or
Diffie-Hellman , on a finite field, the fastest algorithm
is the General number field sieve whose complexity, roughly,
for large
is
.In practice, the smaller ECC keys speed up cryptographic
operations by a factor of
compared to RSA and Diffie-Hellman (in
addition to facilitating their exchange among people and saving
bandwidth). However, there are also disadvantages to ECC
compared to RSA, for example: its signature algorithm
depends on the generation of an additional ephemeral key pair by a
random number generator that, if its output is predictable or
repetitive, reveals the private signature key!
ECC is newer, so:
RSA, andCerticom).Which minimal key size is currently recommend as secure for
RSA and Diffie-Hellman?
512 bits1024 bits4096 bitsWhich minimal key size is currently recommend as secure for Elliptic Curve Cryptography?
128 bits512 bits1024 bitsWhich minimal key size is currently recommend as secure for
AES?
128 bits256 bits1024 bitsRainbow tables are a method of password cracking that compares a password hash to precomputed hashes of the most likely passwords; a time-memory trade-off: more memory for less computation.
A lookup table is a data structure, usually an array, used to replace a runtime computation by an array indexing operation. That is, a value is first computed and then looked up to save runtime, because retrieving a value from memory is usually faster than computing it. For example, values of a common mathematical function, say the logarithm, can be precomputed to look up a nearby value be from memory.
A rainbow table is a table of cryptographic hashes of the most common passwords. Thus, more likely passwords are revealed sooner. The generation of the table depends on
Common cryptographic hash algorithms such as MD4/5,
SHA … are fast; thus they are unsuitable for
password creation because they are vulnerable to brute-force attacks.
For example, MD5 as a cryptographic hash function is
designed to be fast and thus lends itself towards a rainbow table
attack, while hash functions such as PBKDF1,
PBKDF2, bcrypt, scrypt and the
recent Argon2 were designed to prevent this kind of attack
by being:
bcrypt,scrypt.A rainbow attack can however most effectively be prevented by making
the used hash function unique for each password. This is achieved by
adding a salt, an additional unique, usually random,
argument.
The key size of the symmetric industry standard cryptographic
algorithm DES was merely 56 bits, so little
that it ceded to brute-force attacks shortly after its vetting.
Therefore, a twofold encryption for two different keys was thought to
effectively double the key size to 112 bits. However, the
meet-in-the-middle attack by Diffie and Hellman trades off memory for
time to find the key in only
encryptions (using around
stored keys) instead of the expected
encryptions: Assume the attacker knows a plaintext
and its ciphertext
, that is,
where E denotes the
encryption using
respectively
. The attacker:
Therefore, triple encryption, 3DES was necessary to
effectively double the key size and harden decryption for the computing
power to come.
Asymmetric cryptography uses mathematical methods, more exactly modular arithmetic, to encipher. The security, the difficulty of deciphering, of asymmetric cryptography is based on computational mathematical problems that have been recognized as difficult for centuries. Symmetric cryptography (like hash functions) uses more artisanal methods of ciphering, which aim to maximize diffusion and confusion, mainly by iterated substitution and permutation. The security of symmetric cryptography is simply based on its resistance to years of ongoing attacks. That is, it is satisfactory from a practical standpoint, but less so regarding the struggle for eternal truths.
Plaintexts generally do not occur with the same probability. It depends, for example, on the language, jargon or protocol used. A cipher is perfectly secure if none of its ciphertext reveals anything about the corresponding plaintext. That is, the probability that a plaintext and a key resulted in a given ciphertext is the same for all plaintexts and all keys.
perfect security: the probability that a plaintext and a key resulted in a given ciphertext is the same for all plaintexts and all keys.
More exactly: A cipher is called perfectly secure if, for every plaintext, its probability is (stochastically) independent of any ciphertext. Let denote a plaintext and by its probability. In formulas, for every plaintext and every ciphertext , we have . In practice, this means that if an attacker intercepts a ciphertext , then he has no advantage, that is, his probability of knowing the plaintext is the same as if he does not know .
In 1949, Shannon proved the following theorem on the conditions for a cipher to be perfectly secure: Given a finite number of keys and plaintexts with positive probabilities, that is, for every plaintext . The cipher is perfectly secure, if
That is, statistical deviations tend to weaken the cipher. In particular, it is important to use a completely random number generator for the keys.
The only perfectly secure cipher is the one-time pad where a key (of the same size as the plaintext) is added (bit by bit) to the plaintext. Such a perfectly secure cipher is however impractical. For real-time applications, such as on the Internet, it is little used.
The One-time pad adds (by the XOR
operation) each bit of the plaintext
with the (positionally) corresponding bit of a key
that
One-time pad: The key is as long as the plaintext and they are added letter by letter (or bit by bit) to obtain the ciphertext.
That is, the ciphertext is This cipher is as safe as theoretically possible!
If the plaintext has a single block
, then this simple (XOR ) addition of a key, the
one-time pad , is a secure algorithm. However, it is often
inconvenient or even close-to impossible to have a key as large as the
plaintext: For example,
In practice, imagine an agent duplicating gigabytes of noise on two
storage media, for example, a hard disk and a flash drive, and taking
one of these media to encrypt his communication by the
one-time pad.
Unfortunately, it is a bad idea (though natural) to use the same key
for two different blocks: if, for example, the plaintext has
two blocks
and
, then, with this algorithm, the sum (XOR)
of the two cipher blocks
and
equals the sum
of the two clear blocks (because the addition XOR is by
definition auto-inverse, that is
regardless of whether the binary digit is
or
)!

It can be seen as the ciphering of the first block by
one-time pad whose key is the second block. Unfortunately,
the second block is not a good key, because far from being random; on
the contrary, usually its content is similar to that of the first block,
that is, the key is predictable.
As perfect security is unfeasible, security is demonstrated
Although there are provenly secure symmetric ciphers the most
efficient and widely used algorithms, such as AES, prove
their resistance only against known attacks, such as those of
differential or linear cryptanalysis.
The mathematical problems on which the difficulty of the decryption
in asymmetric cryptographic algorithms are based, are all
NP-complete, that is, its solutions are verifiable in
polynomial runtime (in the bit-length of the input) and all other such
problems can be reduced to it. That is, every cryptographic algorithm
(enciphers or) deciphers a message with the key in polynomial
runtime in the bit-length of the key.
In contrast, all known algorithms for deciphering without the key take exponential time in the bit-length of the key. By the P-versus-NP conjecture, there is no algorithm that takes polynomial runtime (in the bit-length of the key). For now, the conjecture being unresolved, there may theoretically exist polynomial algorithms for deciphering without the key in polynomial runtime; however, after decades of continuous vain efforts by the community of cryptanalysts, it is assumed unlikely.
Example. The initial example of such a provenly secure cipher was semantic security (in Goldwasser and Micali (1984)) which reduces the difficulty of decipherment to that of the computation of the Quadratic Residue: Given and a product of two primes, it is difficult to determine whether is quadratic modulo (that is, whether there is such that or not) if, and only if, the so-called Jacobi symbol for is and the prime factors of are unknown.
This (Goldwasser-Micali) cipher consists of:
a key generation algorithm that produces
a probabilistic encipherment algorithm: If are the bits of the plaintext, then numbers , , … that are indivisible by and are generated and the enciphered message is with , , …
a deterministic decipherment algorithm: If is the enciphered message, then if, and only if, is quadratic modulo , … which is quickly determined by knowledge of both factors and of .
Caution: Theoretical security remains an insufficient idealization for reality: For example, Ajtai and Dwork (1999) presented a cipher and proved it theoretically secure; however, it was broken a year later. Proven does not mean true: a provenly secure system is not necessarily truly secure, because the proof is made in a formal model which assumes
For example,
Besides, the proof may be wrong! Despite this uncertainty, a proof of security is a useful criterion (though theoretically necessary, but practically insufficient) for the security of a cipher.
What does security mean? The criterion that the attacker cannot derive the plaintext from the ciphertext is insufficient, because he could acquire other useful (partial) information about the plaintext. But even the impossibility to derive useful information on the plaintext is insufficient in some circumstances: If
RSA encryption as implemented in a textbook) andthen he can encrypt all these possible plaintexts with the public key and compare the ciphertexts to the encrypted texts. For an asymmetric algorithm, the attacker should be assumed to know the public key. Thus, he can encrypt any plaintext of his choice and compare it to the ciphertext; that is, he can mount a Chosen-Plaintext Attack (CPA).
Generally, the attacking scenarios are categorized by how much the cryptanalyst’s knows about the ciphertext (ordered below from less to more knowledge):
For example, to break a monoalphabetic cipher, the ciphertext alone usually suffices thanks to frequency analysis. But often the cryptanalyst either will know or can guess some of the plaintext, such as a preamble of a letter (like a formal greeting) or a computer file format (like an identifier). Lastly, most opportunely, he can ask the sender to encrypt a plaintext that he chose or the recipient to decrypt a ciphertext that he chose.
The attacker has the ciphertexts of several messages that were encrypted by the same algorithm. His task is to recover as much plaintext as possible or, better, to recover the (algorithms and) keys that were used.
The attacker has the ciphertext and suspects that the plaintext
contains certain words (a crib) or even whole sentences. His
task is to recover as much plaintexts as possible or, better, to recover
the (algorithms and) keys that were used. For example, Enigma, the
cryptographic electromechanical rotor-machine used by the power axes in
World War II, was broken by the repetitiveness of the messages it
enciphered: for example, the weather report was sent on a daily basis
and announced as such (Wetterbericht in German) at the
beginning of every such message.
crib: a text probably contained in the plaintext of a given ciphertext.
The attacker has a ciphertext and the corresponding plaintext. His
task is to recover the (algorithm and) key that was used. (For example,
linear cryptanalysis falls into this scenario). For example, an attack
from 2006 on the Wired Equivalent Privacy (WEP) protocol
for encrypting a wireless local area network exploits the predictability
of parts of the encrypted messages, namely the headers of the
802.11 protocol.
The attacker has the ciphertexts of the plaintexts that he can freely choose; so that the attacker can freely adapt the plaintext depending on the text obtained after each decipherment and analyze the resulting changes in the ciphertext. His task is to recover the (algorithm and) key that was used. (For example, differential cryptanalysis falls into this scenario).
This is the minimal attacking scenario to be prepared against for
asymmetric cryptography! Since the encryption key is public, the
attacker can encrypt messages at will. Therefore, if the attacker can
reduce the number of possible plaintexts, for example, if he knows that
they are either “Yes” or “No”, then he can encrypt all possible
plaintexts by the public key and compare them with the intercepted
ciphertext. For example, the RSA algorithm in its textbook
form suffers from this attack. Therefore, to protect against this
CPA attack, every implementation of this algorithm must pad
the plaintext with random data before encryption.
The attacker has a ciphertext and the plaintexts of the ciphertexts (except ) that he can freely choose; so that the attacker can freely adapt the plaintext depending on the text obtained after each decipherment and analyze the resulting changes in the ciphertext. His task is to recover the (algorithm and) key that was used. For example, the attacker has to analyze a cipher machine black-box, that is, whose inner workings are unknown.
Few practical attacks fall into this scenario, but it is important for proofs of security: If resistance against the attacks of this scenario can be proven, then resistance against every realistic attack of chosen ciphertext is granted.
If an asymmetric algorithm is used, then the attacker should be
assumed to know the public key. Thus, he can encrypt any plaintext of
his choice and compare it to the ciphertext. That is, he can mount a
chosen-plaintext attack (CPA).
A cipher is secure against IND-CPA
(indistinguishability of the ciphertext for chosen plaintexts),
if no attacker can distinguish which one of two plaintexts, that he
selected before, corresponds to the ciphertext that he receives
afterwards. More exactly, the cipher is indistinguishable under
chosen-plaintext attack if every probabilistic polynomial-time
attacker has only an insignificant “advantage” over random guessing:
IND-CPA-secure: no attacker has a probability significantly higher than to distinguish two ciphertexts.
The four steps of the game IND-CPA with
polynomial-runtime restriction (in the bit-length of the key
) on the attacker’s computations (carried out on creating the two
plaintexts, step two, and on choosing the plaintext that corresponds to
the ciphertext, step four):
A pair of keys is created, one secret and one public, both with bits. The attacker receives the public key.
The attacker computes two plaintexts and of the same size.
The cipher machine
The attacker chooses a bit in .
The attacker who chooses the bit
in the fourth step randomly is right with a probability of
. A cipher is IND-CPA-secure if no
attacker has a probability of success
significantly higher than
:
That is, if every attacker’s difference
is insignificant, that is: for every (nonzero) polynomial
function
there is
such that
for every
.
An insignificant difference should be granted, because the attacker easily increases his probability of success above by guessing a secret key and trying to decipher the ciphertext with it.
Observation. Although the above game is formulated for an asymmetric cipher, it can be adapted to the symmetric case by replacing the public key cipher by a cryptographic oracle, a black-box function, that is, whose inner workings are unknown, that retains the secret key and encrypts arbitrary plaintexts at the attacker’s request.
Secure semantic encryption algorithms include El Gamal and
Goldwasser-Micali because their semantic security can be
reduced to solving some difficult mathematical problem, that is,
irresolvable in polynomial runtime (in the number of input bits); in
these cited examples, the Decisory Diffie Hellman Problem and
the Quadratic Residue Problem. Other semantically insecure
algorithms, such as RSA, can be made semantically secure by
random cryptographic paddings such as OAEP (Optimal
Asymmetric Encryption Padding).
Example. The Elgamal encryption method is
IND-CPA-secure under the assumption that the Decisory
Diffie Hellman Problem is difficult. To prove security, let us
transform
A from the IND-CPA game
for El Gamal , that is, given the ciphertext of one among
two plaintexts under the public key, she identifies the corresponding
plaintext (among the two) with probability
),S for DDH , that is,
given a base
and exponents
,
and
in
, she decides in polynomial runtime whether
or not;as follows: Given a base and exponents , and in .
S simulates the creation of a key pair by giving
as public key to A (but not knowing the corresponding
secret key).A produces two plaintexts
and
.S simulates the encipherment by randomly choosing a bit
and defining the ciphertext as
.A decides whether the plaintext is
or
.A wins with probability
.A just guesses and wins with probability
.S ’s strategy is therefore to opt for
if, and only if, A is correct. Thus, the probability that
S is correct is
.
Let us recall that:
IND-CPA
(indistinguishability of ciphertext for chosen plaintexts), if
no attacker can distinguish which one of two plaintexts, that he
selected before, corresponds to the ciphertext that he receives
afterwards.CCA the attacker has a ciphertext
and the plaintexts of the ciphertexts (except
) that he can freely choose;A cipher is secure against IND-CCA (indistinguishability
of ciphertext for chosen ciphertexts), if the attacker, in the
second and fourth steps of the IND-CPA game, can ask for
any ciphertext to be deciphered (except the one in question
), and still cannot distinguish which one among two plaintexts
corresponds to the ciphertext:
The oracle creates a secret key.
The attacker asks for the decryption of any ciphertext (except ), and creates two plaintexts and of equal size.
The oracle
The attacker asks for the decryption of any ciphertext (except ), and chooses a bit in .
Example. Bleichenbacher’s attack on
PKCS#1 from 1998 is secure against the RSA
variant of IND-CPA (but precisely not against IND-CCA!).
Bellare and Namprempre showed in 2000 for a symmetric cipher that if
IND-CPA, andthen the cipher with “Encrypt-then-MAC” resists an “IND-CCA” attack.
Is the one-time pad perfectly secure in theory?
What are all known perfectly secure cipher in theory? one-time pad
Is the one-time pad perfectly secure in practice?
What is a practical inconvenience of the one-time pad? Its key must be as long as the plaintext.
A side-channel attack uses information from the physical implementation of a cipher machine. For example, measures of timing, power consumption, electromagnetic or sound emissions.
side-channel attack: an attack that uses information on the physical implementation of a cipher machine.
We will restrict to timing attacks that measure the runtimes of cryptographic operations (of a specific software on a specific hardware) and compare them to estimated ones. A timing attack can be carried out remotely, however, the measurements often suffer from noise, that is, random disturbances from sources such as network latency, disk drive access times, and correction of transmission errors. Most timing attacks require that the attacker knows the implementation; however, inversely, these attacks can also be used to reverse-engineer.
timing attack: an attack that measures the runtime of cryptographic operations and compares them to estimated ones.
We will restrict to the example of a timing attack that measures the time for computing integer powers. For this, we first have to understand how integer powers are computed:
Exponentiating by squaring (or square-and-multiply algorithm or binary exponentiation) is an algorithm to quickly compute large integer powers of a number by binary expansion of the exponent; especially useful in modular arithmetic. To compute , instead of multiplying by itself times, only multiplications are needed:
Exponentiating by squaring (or square-and-multiply algorithm or binary exponentiation): an algorithm to quickly compute integer powers of a number by binary expansion of the exponent.
Given a nonnegative integer base and exponent , to compute :
Because
, that is, each power is the square of the previous one (and at
most M ), each power, one after the other, is easily
computable, yielding:
(In hindsight, only powers
with
equal to 1 count, the others can be omitted.)
Example. To calculate , expand and calculate yielding
The execution time of binary exponentiation depends linearly on the
number of bits equal to 1 in the exponent. While the number
of these bits alone is insufficient information to find the key,
statistical correlation analysis (and the Chinese remainder theorem) on
exponentiations with different bases (but the same exponent) derives the
exponent.
Crypto-algorithms that encipher using exponentiation modulo a large
prime number, and as such are vulnerable to this attack, include
RSA, Diffie-Hellman and ElGamal
and the Digital Signature Algorithm (that derives from the former).
For example, in (textbook) RSA , the message is the base
and the key is the exponent
. Brumley
and Boneh (2005) demonstrated a network-based
timing attack on SSL-enabled web servers using RSA that successfully
recovered the private key in a day; this lead to the widespread
deployment of concealment techniques to conceal correlations
between key and encryption time.
Kocher (1996) exposed a flaw in the following algorithm to compute modular exponentiation, that is, to compute for public and known, but secret. The attacker, by computing for several values of and knowing , and the computation time, can derive as follows:
Let w be the bit length of x and put s_0 = 1.
For k ranging from 0 to w-1:
If the k-th bit of x is 1, then
put R_k = (s_k * y) mod n;
Otherwise,
put R_k = s_k.
Put s_{k+1} = R_k^k mod n
End (of For loop)
Return (R_{w-1})According to the value of the -th bit of , either or nothing is computed; therefore, the execution time of the algorithm, for different values of will eventually yield the value of the -th bit.
To prevent this attack, the algorithm can be changed so that all calculations, whatever the key bits, take the same time (slowing it down, but, security counts more than speed):
Let w be the bit length of x and put s_0 = 1.
For k ranging from 0 to w - 1:
Put temp = (s_k y) mod n.
If the k-th bit of x is 1, then
put R_k = temp;
Otherwise,
put R_k = s_k.
Put s_{k+1} = R^2_k mod n.
End (of For loop)
Return (R_{w-1})To understand the reasons behind the design choices of each step of a
block cipher algorithm, such as AES, one must understand
which attacks it defies. A powerful modern cryptanalytic algorithms is
differential cryptanalysis, applicable to block ciphers. It assumes a
chosen-plaintext attack: The attacker sends pairs of (slightly)
differing plaintexts, whose ciphertexts he receives. He then studies how
differences in the input propagate (on so-called differential trails)
through the network of encipherment transformations to differences at
output. The resistance of AES against this resistance by so-called wide
trails was proved in the paper of proposal Daemen and Rijmen (1999).
Let us demonstrate this technique in the toy model of a Feistel Cipher given in Heys (2002) that
16 bits, and4 blocks of 4
bits.For each round, there is a corresponding (independent) key. In each
one of the first three rounds 1, 2 and
3:
Add the round key to the block , in formulas: .
Substitute each of the 4 sub-blocks bits according
to the table (in hexadecimal notation)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 4 | D | 1 | 2 | F | B | 8 | 3 | A | 6 | C | 5 | 9 | 0 | 7 |
Swap bit from the sub-block with from the sub-block ;
In the penultimate 4th round:
4 sub-blocks of 4
bits with the table.In the last 5th round
That is:
5th round, the last two steps, substitution
and permutation, are omitted, because, the algorithm being public
(following Kerckhoff’s principle), can be undone by any decipherer
without knowledge of the key. That is, from a cryptographic point of
view, they are superfluous.4th round, the last step, the permutation, is
omitted as it would only permute the last 5th round key.
That is, from a cryptographic point of view, it is superfluous.The substitution table originates from the DES algorithm
and is commonly called the S-box, Substitution box.
A cryptanalyst’s dream is to learn whether a part of the chosen key
is correct, that is, whether it coincides with the
corresponding part of the key used to encrypt the text: For example, in
Heys’s cipher the key has 16 bits: If one could learn
whether, say, one half (8 bits) of the whole key tried out
matches the corresponding half of the correct key, then the
cryptanalyst
8 bits (of which there are
) and the remaining 8 bits (of which there are
).That is, the number of combinations that need to be tested out has been reduced from to .
In a brute-force attack, the cryptanalyst deciphers the enciphered text with each possible key. To know whether the key tried out is correct, that is, if it coincides with the key used to encrypt the text, he checks whether the content is intelligible; for example, by a criterion such as
If the cipher has a single round, then this criterion is applicable. However, if the cipher has two or more rounds, and the decipherer executes the last round of the decryption algorithm with a certain key, then this criterion is no longer applicable, because the text obtained is the output of the encryption algorithm (with the same key) from the penultimate round. Instead, the criterion of differential cryptanalysis for having found the correct key is probabilistic: the key tested out is probably correct if, for a certain “incoming” difference and a certain “outgoing” difference , plaintext pairs with difference result with a certain probability in cipher pairs with difference .
For differential cryptanalysis to be applicable, the cryptanalyst must be able
Differential cryptanalysis exploits the high probability of a
difference
between two plaintexts
and
propagating to a difference
between the two ciphertexts
and
(for
and
) (in the penultimate round); here
is the addition XOR , bit per bit, where the output is
1 if, and only if, the two entries are different. (In
particular, the addition XOR is auto-inverse, that
is, the reverse operation to
is
;
in contrast to the
operation with its reverse
. Therefore, the difference is given by the addition
XOR. That is,
, indicates all the bits in which
and
differ.) The pair
is the differential.
The difference of and is
A differential is a pair of input respectively output differences respectively .
For differential cryptanalysis to be efficient, there must be a differential with high probability (to be quantified in Equation 12.1); that is, among all incoming pairs with difference , the probability of an outgoing pair having difference (in the penultimate round) is . More exactly, the encipherer will encipher a statistically significant number of pairs () of plaintexts with difference to count the number of the enciphered pairs of ciphertexts with difference .
An affine transformation A is the
composition
Observation. For an affine transformation , the outgoing difference is independent of the incoming pair and (but only depends on ): The transformation :
Regarding the first and second function of each round of a Feistel cipher:
that is, the outgoing difference is independent of the incoming pair. However, the outgoing difference of the substitution is not determined by the incoming difference alone, but it depends on and ! We examine the substitution table to find a differential of high probability , that is, to find an incoming difference with a large number of pairs and that yield an outgoing difference : Given , there are possible inputs (which determines ), and we count the frequencies of the possible outgoing differences :
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
1110 |
0100 |
1101 |
0001 |
0010 |
1111 |
1011 |
1000 |
0011 |
1010 |
0110 |
1100 |
0101 |
1001 |
0000 |
0111 |
This table lists the outgoing differences of each incoming pair whose
difference is one of 1011, 1000 or
0100 :
1011 |
1000 |
0100 |
|
|---|---|---|---|
0000 |
0010 |
1101 |
1100 |
0001 |
0010 |
1110 |
1011 |
0010 |
0111 |
0101 |
0110 |
0011 |
0010 |
1011 |
1001 |
0100 |
0101 |
0111 |
1100 |
0101 |
1111 |
0110 |
1011 |
0110 |
0010 |
1011 |
0110 |
0111 |
1101 |
1111 |
1001 |
1000 |
0010 |
1101 |
0110 |
1001 |
0111 |
1110 |
0011 |
1010 |
0010 |
0101 |
0110 |
1011 |
0010 |
1011 |
1011 |
1100 |
1101 |
0111 |
0110 |
1101 |
0010 |
0110 |
0011 |
1110 |
1111 |
1011 |
0110 |
1111 |
0101 |
1111 |
1011 |
Let us count, for every incoming difference , how many times each outgoing difference appears among all the incoming pairs and such that .
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 4 | 0 | 4 | 2 | 0 | 0 |
| 2 | 0 | 0 | 0 | 2 | 0 | 6 | 2 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 |
| 3 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 4 | 2 | 0 | 2 | 0 | 0 | 4 |
| 4 | 0 | 0 | 0 | 2 | 0 | 0 | 6 | 0 | 0 | 2 | 0 | 4 | 2 | 0 | 0 | 0 |
| 5 | 0 | 4 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 2 |
| 6 | 0 | 0 | 0 | 4 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 2 |
| 7 | 0 | 0 | 2 | 2 | 2 | 0 | 2 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 4 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 0 | 4 | 2 | 2 |
| 9 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 4 | 2 | 0 | 2 | 2 | 2 | 0 | 0 | 0 |
| A | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 2 | 0 | 0 | 4 | 0 |
| B | 0 | 0 | 8 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 |
| C | 0 | 2 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 6 | 0 | 0 |
| D | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 4 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| E | 0 | 0 | 2 | 4 | 2 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| F | 0 | 2 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 2 | 0 |
The entries for each row add up to , the number of all possible pairs for a given difference. The first row confirms that two equal inputs result in two equal outputs. The highest number is and reached for and . In addition, the number comes up five times.
We will choose our differentials among those with these high frequencies:
Example. In the frequency table
Given a Feistel cipher, a differential trail is a
finite sequence of differences
so that every entry
is the input of the S-box of the
-th cipher round. Given the outgoing difference
of the S-box of round
, the incoming difference of the next round
is the result of applying the permutation to
. (The key addition, as a translation, does not change the
difference.)
differential trail: a tuple of differences , , … so that every entry is the input of the
S-boxof the -th cipher round.
We want to find the most probable differential trail in the Heys cipher or at least a trail in which each differential is among the most probable. Every differential consists of sub-differentials, corresponding to the sub-blocks of bits that constitute block of bits. To find such a probable differential trail, in each round:
S-box transforms the incoming
difference (of the sub-differential) into the outgoing difference;An example of such a trail
is the following: Let the difference in the first round be
which is by S-box
2 replaced by
By the subsequent permutation, we
obtain as difference entering the second round
which is by S-box
3 replaced by
Because the bits number
and
are nonzero, we obtain by the subsequent permutation as incoming
difference of the third round that with two active sub-differentials
which is by S-boxes
2 and 3 replaced by
Finally, by the subsequent permutation,
the fourth round input is
Let
denote the substitution of the sub-block
by the S-box in the
-th round. On our differential trail, we enlist
the probability of substitution transforming the incoming difference (in hexadecimal notation) into outgoing difference :
| Substitution | In | Out | Probability |
|---|---|---|---|
| S12 | B |
2 |
8/16 |
| S23 | 4 |
6 |
6/16 |
| S32 | 2 |
5 |
6/16 |
| S33 | 2 |
5 |
6/16 |
If we suppose that the differentials of one round are independent of the differentials of the previous round (which is a negligibly inaccurate simplification), then the probability of the concatenated substitutions transforming into is the product of the probabilities of each substitution,
To find the key, for
the cryptanalyst
S-box input in the fourth
round by the round key
to obtain the pair
and
with difference
,
andIf for a combination of sub-blocks and the count yields , that is, the ratio between
is close to the probability
,
then these sub-blocks are probably the sub-blocks 2 and
4 of the round key 5 used by the cipher.
Observation. To conclude that we found the correct sub-blocks, we use the hypotheses
Both have no rigid mathematical foundation, but are only plausible, because, respectively:
Note that for this attack to be faster, that is, to be more effective, than the brute-force attack (which simply tries out all possible keys), it is necessary that where
2 and 4),16 bits
in this figure).Therefore, it is necessary that the trail is strict, that
is, has few active blocks, in order to be able to learn whether the
tested key is correct, that is, coincides with the key used, only in
these active blocks (which reduces the number of combinations
logarithmically). In the example given, only 2 out of the
4 sub-differentials are active, which allowed the
cryptanalyst to learn whether the key is correct in only these
2 blocks: the number of combinations that need to be proved
was accordingly reduced from
to
.
S-box of the
-th cipher round.S-box replaces the incoming difference
with the outgoing difference of the sub-differential.Cryptanalysis is the art of breaking ciphers, that is, recovering or forging enciphered information without knowledge of the key. Historically, the cryptanalyst’s intuition and ability to recognize subtle patterns in the ciphertext were paramount. Today, however, cryptanalysis is based on mathematics and put into practice by efficient use of extensive computing power.
In practice, the security of a cipher, and thus the recommended key sizes, relies foremost
It the secret information, for example, passwords, was stored as
cryptographic hashes, then a practically more efficient brute-force
attacks uses a rainbow table, a table of the cryptographic hashes of the
most common passwords to reveal more likely passwords sooner. This is
particularly promising against quickly computed hash functions such as
MD4/5, whereas hash functions used for hashing passwords,
such as bcrypt, were designed to be deliberately slow. Such
a rainbow attack is however most effectively prevented by making the
used hash function unique for each password by adding a
salt, an additional unique, usually random, argument.
The only perfectly secure cipher is the one-time pad where a key (of the same size as the plaintext) is added (bit by bit) to the plaintext; too unwieldy to be useful in practice.
Asymmetric cryptography uses mathematical methods, more exactly modular arithmetic, to encipher. The security, the difficulty of deciphering without knowledge of the key, of an asymmetric cryptographic algorithm is based on mathematical problems that have been established as computationally difficult. Symmetric cryptography (like hash functions) uses more artisanal methods of ciphering, which aim to maximize diffusion and confusion, mainly by iterated substitution and permutation. The security of symmetric cryptographic algorithms is simply based on its resistance against years of ongoing attacks.
A side-channel attack uses information from the physical implementation of a cipher machine. For example, measures of timing, power consumption, electromagnetic or sound emissions. In particular, a timing attack measures the runtimes of cryptographic operations, and compares them to the estimated ones. For example, one exploits that the runtime of the computation of a power depends on the number of nonzero bits of its exponent (which, in RSA and Diffie-Hellman is the key).
Among all modern cryptanalytic algorithms, one of the most powerful ones is differential cryptanalysis that applies to block ciphers and assumes a chosen-plaintext attack: The attacker sends pairs of (slightly) differing plaintexts whose ciphertexts he receives. He then studies how differences on input propagate (on so-called differential trails) through the network of encipherment transformations to differences at output. The resistance of AES against this resistance by so-called wide trails was proved in the paper of proposal Daemen and Rijmen (1999).
Which minimal key size is currently recommend as secure for
RSA and Diffie-Hellman?
512 bits1024 bits4096 bitsWhich minimal key size is currently recommend as secure for Elliptic Curve Cryptography?
128 bits160 bits512 bitsWhich minimal key size is currently recommend as secure for
AES?
80 bits128 bits256 bitsWhich computationally difficult problem is the security of
RSA based on?
prime number decomposition, discrete logarithm, point counting, quadratic residue
Which computationally difficult problem is the security of the Diffie-Hellman key exchange based on?
prime number decomposition, discrete logarithm, point counting, quadratic residue
Read Heys (2002) to understand the basic principles of differential cryptanalysis.
Read the submissions Daemen and Rijmen (1999) and Daemen and Rijmen (2002)
that present the algorithm AES and show its security by its
resistance against differential cryptanalysis.
On completion of this chapter, you will have learned …
TLS, S/MIME or PGP, andongel.de are looked up and how
this look can be authenticated and encrypted by Secure DNS.While before the Internet age it was unimaginable to use cryptography in everyday life, today everyday life on the Internet would be unimaginable without (public-key) cryptography; for example, for securely shopping online. Besides ciphering, cryptography establishes trust where previously paper documents were used, for example, for signing, identity authentication, granting authority, license, or ownership. And cryptography achieves this more securely so: While a written signature is imitable, a digital signature is uniquely linked to (the contents of) the signed document.
To secure transactions on the Internet, for example, in electronic banking, commerce or mailing, a cryptographic protocol (such as Transport Layer Security, TLS, formerly Secure Sockets Layer, SSL):
X.509 certificates. The various protocols that standardize the processing of exchanged data on the Internet can be grouped into layers, ordered according to how highly structured the processed data is:
Among these protocols, the two most important protocols (and those that were defined first) are
that specify how data should be formatted, addressed, transmitted, routed and received at the destination. Though the TCP/IP protocol reliably delivers data packets over the Internet, it
Most Internet applications rely on a higher (application) layer, such as the HTTP protocol for Web servers.
The best known stacks of such layers of Internet protocols are:
OSI model: model by the International Standards Organization (ISO) that stacks the various protocols of the Internet protocol suite into seven abstraction layers.
Internet Protocol Suite: TCP/IP stacks the various protocols of the Internet protocol suite into four layers.
First, the Internet is not to be confused with the World Wide
Web (WWW, for short the Web) which is an application of the
Internet, albeit the most popular serves linked documents. A web
document is written in HyperText Markup Language (HTML),
transmitted by the HyperText Transfer Protocol (HTTP) and
retrievable at an online address called a Uniform Resource Locator
(URL). The web does not include, for example, e-mail,
instant messaging and file sharing.
World Wide Web: an application of the Internet that serves on a graphical user interface linked documents written in HyperText Markup Language (HTML), transmitted by the HyperText Transfer Protocol (HTTP) and retrievable at an online address called a Uniform Resource Locator (URL).
Originally, the Web was developed to let scientists around the world
exchange information instantly. In 1989, English computer scientist
Timothy Berners-Lee developed at the Conseil Européen pour la Recherche
Nucléaire (CERN, the European Organization for Nuclear
Research) the first Web server and client, a hypertext browser and
editor, and specified the URL, HTTP and
HTML formats on which the Web depends. The Web was made
available within CERN in December 1990 and on the Internet at large in
the summer of 1991. (Since 1994, Berners-Lee is Director of the W3
Consortium, which coordinates Web development worldwide.)
The Internet itself evolved out of an early wide area network called
ARPAnet: President Dwight D. Eisenhower saw the need
for the Advanced Research Projects Agency (ARPA), after the Soviet
Union’s launch of Sputnik, world’s first satellite, in 1957. The ARPA
followed suite by developing the United States’ first successful
satellite in 18 months. Several years later ARPA developed computer
network of funded research laboratories that eventually evolved into
ARPAnet in the 70s. It was expanded in the United States to
some laboratories and academic institutions, and then to Europe, where
the European Organization for Nuclear Research (CERN) was one of the
nodes.
ARPAnet: computer network developed by the Advanced Research Projects Agency (ARPA) between a number of laboratories and academic institutions
A driving force behind the creation of the ARPAnet was the desire to share computer resources more efficiently:
Computer time in the 50s was so costly access time had to be limited and scheduled. Much time on the computer was used for input and output, but not computing, so the computing power often went unused, and the computer was practically idle. To use computer resources more efficiently, the idea of “Time-sharing” to run multiple programs (seemingly) “at the same time” was born: The computer switched from user to user while receiving input or returning output, giving them the impression of a live interaction with the computer instead of taking turns. The Ethernet protocol was created (by the Xerox Corporation) to connected different computers into a single (so called local-area) network. These interactions then took place on a local area network, but the more users, the less responsive the computer.
The idea was born to share computational resources by connecting various local networks to a single larger network. In 1966 the Information Processing Techniques Office (IPTO) funded the creation of a high-speed network among the funded research laboratories, which eventually evolved into the ARPANET that differed from existing computer networks by:
Such a decentralized network, without critical paths, sparked the interest of the military, since it could reroute messages even if part of the network was destroyed (while the destruction of a telephone operation center entails that of its entire dependent network).
The American computer scientist Vinton Cerf at Stanford University wrote the first TCP protocol with Yogen Dalal and Carl Sunshine, called Specification of Internet Transmission Control Program (RFC 675), published in December 1974. From 1972-1976, Cerf co-designed the TCP/IP protocol-suite with Robert Kahn that would form the basis of the Internet. Cerf worked at the United States Defense Advanced Research Projects Agency (DARPA) from 1976 to 1982 and funded various groups to develop TCP/IP. When Robert Kahn became IPTO director in 1979, the DARPA had multiple incompatible packet-switching networks, which on 1 January 1983, adopted the suite of TCP/IP protocols. After some demonstrations of the network technology, such as linking the networks of SATNET, PRNET and ARPANET from Menlo Park, CA to University College London and back to USC/ISI in Marina del Rey, CA in November 1977, the Internet started in 1983.
Since the Internet runs on the TCP/IP reference-model, which has only four layers, the standard ISO 7-layer stack is more of a theoretical abstraction than a practical standard. Unlike the standard ISO 7-layer stack, the TCP/IP 4-layer stack evolved by being used rather than drafted and thus is testified to work, even cross-platform. While the Internet Protocol Suite is descriptive, the OSI reference-model was intended to be prescriptive: the OSI model is a wonderful abstract construction; though the network, which exists and works, does not fully follow it. However, the iOS Model is of historical and conceptual interest, as it precedes the former, and the same principles apply.
When the models are (incorrectly) used interchangeably, both are referred to as the Internet reference-model.
| OSI Layer | TCP/IP Layer | Examples |
|---|---|---|
| Applications (7) | Applications (4) | HTTP(Hypertext Transfer
Protocol FTP(File Transfer Protocol)
SMTP(Simple Mail Transfer) IMAP(Instant
Message Access Protocol) DHCP(Dynamic Host
Configuration) |
| Presentation (6) | ||
| Session (5) | SOCKS (Socket Secure) |
|
| Transport (4) | Transport (3) | TCP Transmission Control
Protocol) UDP(User Datagram Protocol) |
| Network (3) | Internet (2) | IPv4/6(Internet Protocol)
ICMP(Internet Control Message) |
| Data Link (2) | Network Access (1) | IEEE 802.3 (Ethernet LAN)
IEEE 802.11,802.11a -- g (Wi-Fi) |
| Bit Transmission (1) |
However, different application protocols (such as HTTP, FTP, IMAP, …)
implement the functions of Layer 5, 6 and
7 differently, and do not separate these layers strictly;
hence, practitioners, such as network engineers, subsume all those
layers as Layer 5+, the application layer, just like the
Internet Protocol Suite does.
A private IP network is a network (commonly a local area networks (LANs) in residential and enterprise environments) whose computers have IP addresses which fall into the ranges specified by IPv4 (in RFC 1918; analogue ones exist in IPv6):
10.0.0.0 to 10.255.255.255,172.16.0.0 to 172.31.255.255,
and192.168.0.0 to 192.168.255.255These addresses can be used without approval from an Internet registry. (Where here and henceforth we often mean computer to mean an endpoint of the network; this includes tablet, smartphones and other network devices.)
Private Network: network that uses private IP addresses without any need of approval from an Internet registry.
A Virtual Private Network (VPN) is a private network made up of (at least) two (spatially separate) closed networks connected via an open network (such as the Internet). For example, to connect
VPN: A private network made up of two or more (spatially separate) closed networks connected via an open network (such as the Internet).
To establish privacy, the connections between two closed networks use authentication and encryption: The parties authenticate mutually using a previously set shared secret (such as a password or certificate); then the exchanged data is encrypted and decrypted at the end points.
Briefly, a gateway is a device that links two networks such as a router that distributes network traffic flow. An internet connection at home usually uses a router to deliver internet data packets to the devices at home, for example, a smartphone, tablet or laptop. This is the first router the device at home connects to for an Internet connection; also known as a default gateway. By convention the gateway has the lowest IP address in the subnet (a group of addresses).
A Firewall filters data packets to protect an inner (private) network from an outside (public) network. It is usually located on a gateway, or possibly as software on a user’s computer, for example, as part of the operating system such as the “Microsoft Windows firewall”.
Many (consumer) devices are both a router and a firewall. Therefore, these three terms, Gateway, Router and Firewall, are sometimes used interchangeably.
Routing is the directing of data packets from their source toward their ultimate destination through intermediary nodes, called routers, over the network. A router is a computer networking device that distributes data packets across a network of (two or more) networks toward their destinations, through a process known as routing, that is,. Routing occurs at layer 3 (the Network layer) of the OSI seven-layer model. To compute the best routes to network destinations the routers use routing tables: a basic routing table stores details of every computer in the network and the connections between them; others also the current state of the network with respect to the amount of traffic.
The simplest routing is hop-by-hop routing: each routing table lists, for all reachable destinations, the address of the next device along the path to that destination; the next hop. If the routing tables are consistent, then the simple algorithm of relaying packets to their destination’s next hop thus suffices to deliver data anywhere in a network. In practice, hop-by-hop routing is now replaced by the newer Multiprotocol Label Switching (MPLS), where a single routing table entry can select the next several hops resulting in less table lookups and faster arrival.
Routing Protocols specify how routers (mutually) exchange the (changes in their) routing tables. In the basic Router Information Protocol (RIP) they are periodically exchanged entirely. Because this is a rather inefficient process, RIP is replaced by the newer Open Shortest Path First(OSPF) protocol (RFC2178 from 1998) which causes smaller, more frequent updates (but require more processing power and memory).
A Firewall is a software that monitors network traffic, usually between two networks, one trusted (for example, a private local-area network at home or at a company), the other one not, (for example, a public wide-area network such as the Internet), to provide security by blocking access from the public network to certain services in the private network. It can run on a multi-purpose device (like a personal computer) or a dedicated device (like a router, especially for larger networks).
A simple Firewall (known as packet filter or screening router) has a set of rules, which are applied to each data packet according to its attached metadata, (where it is from, where it should be sent to, …), to decide whether to allow a packet through. In the simplest case, a firewall only refuses data packets based on its port. It works at the network OSI layer. Simply put, the private network is the castle, the firewall the bulwark and (network) ports holes that have to be drilled into it for access to the public network.
An application-layer firewall not only looks at the metadata but also at the actual data (so-called deep packet inspection, DPI). For example, a user of a private network could install a backdoor trojan by surfing to a Website with malicious code or by opening an email attachment.
A firewall can run on the computer in the private network connected to the public network, for example, on a personal computer running Linux or Windows connected to the Internet. However, the larger the private network, the more points of failure (such as out-of-date or disabled firewalls), including other devices such as a printer or TV. Therefore, it is prudent in larger private networks (such as those in a company) that connect to a public network to have a dedicated firewall for the whole network.
A Gateway is a device, often a dedicated computer, that works as a gateway from the computers of one to those of another network; that is, that joins two different networks, usually an internal (local-area) network to a wide-area network such as the Internet. For example, the connection of a modem to the Internet via an Internet Service Provider (ISP) is shared among the computers of a home or company network via a router or a firewall. For these computers, the router or firewall is the gateway. However, gateway is more general a term than router or firewall, because it takes care of all possible conversions between different network architectures, for example, from one protocol or character encoding to another: say from TCP-IP to a proprietary protocol used by a subnetwork. It works at level 4 and higher of the OSI reference-model.
Network Address Translation (NAT) translates public IP addresses into private ones in an Internet Protocol(IP) network by changing the the source or destination address in every packet header (and adjusting the checksums): It replaces the host’s internal source address in the IP packet header by the NAT device’s external IP address. Typically, NAT is implemented on gateways (such as router or firewalls).
Network Address Translation (NAT): translates the public IP addresses of an IP network into private ones.
Port Address Translation (PAT) replaces the host’s source port number in the TCP (or UDP) header by one from a pool of available ports. The NAT device stores an entry in a translation table that maps the host’s internal IP address and source port to the source port it was replaced with. While the internal host knows the IP address and TCP (or UDP) port of the external host, the external host only knows the public IP address of the NAT device and the port used to communicate with the internal host. However, a host’s internal applications that use multiple simultaneous connections (such as an HTTP request for a web page with many embedded objects) can deplete available ports. To avoid this, the NAT device tracks the destination IP address in addition to the internal port (thus sharing a single local port with many remote hosts).
For peer-to-peer applications such as VOIP and VPNs, external hosts must connect directly to a particular internal host. The internal addresses all map to the same publicly accessible address of the NAT device. This poses no problem if the NAT is a full cone or has Endpoint-Independent Mapping and Filtering (as categorized in RFC 3489 or RFC 4787), that is, maps an internal IP address to a static TCP/UDP port. However, NAT traversal (NAT-T) is needed, for example, if
To this end IPsec-VPN encapsulates Encapsulating-Security-Payload (ESP) packets into UDP packets using port 4500. VOIP employs
-either the Session Traversal Utilities for NAT (STUN) protocol (as specified in RFC5389) that uses hole punching: For Alice to establish a connection to Bob, a public relay server first passes Alice’s public socket (IP address and UDP port) to Bob. Bob then sends an initial (usually rejected) packet to this socket so that Bob’s firewall allows a connection from it (as reply to this outgoing connection), - or, if STUN fails, the Traversal Using Relay NAT (TURN) protocol (as specified in RFC 5766), in which the public relay server not only mediates the socket information but the entire traffic between Alice and Bob.
Most networks use NAT to enable multiple hosts on a private network with different private IP addresses to connect to the Internet using a single public IP address assigned through an Internet Service Provider (ISP). That is, NAT hides an entire (private network) address space behind a single IP address in the public domain address space.
NAT keeps track of the “state” of the network connections and uses translation tables whose entries can be filled by the network administrator (static NAT or port forwarding). This allows traffic originating in the public “external” network to reach selected hosts in the private “internal masqueraded” network. In particular, Port Address Translation (PAT) translates TCP or UDP connections made to a host and port on an outside network (Internet) to a host and port on an inside network (LAN) by mappings different internal IP addresses to different outside ports. This way a single external IP address is used for many internal hosts; almost as many as there are ports: over 64000 internal hosts.
NAT changes the source or destination address in the packet header (and adjusts the checksums). In particular, PAT attaches to an IP packet a new IP address and source port. IPSec authenticates (and encrypts) the data packet, but the Network-Address Translation in-between breaks authenticity:
Because ESP does not use ports that could be “translated”, it fails on networks that use PAT (like common home routers) and only a single client in the local network can establish a VPN tunnel. Therefore connections between hosts in private TCP/IP networks, which use NAT devices; for example, of peer-to-peer and VoIP applications, cannot be established.
NAT Traversal (NAT-T or UDP encapsulation) solves this incompatibility between NAT and IPSec: After detecting one or more NAT devices, NAT-T adds a layer of User Datagram Protocol (UDP) encapsulation to IPsec packets, so they are not discarded after address translation. RFC3947 defines the negotiation during the IKE phase and RFC3948 the UDP encapsulation (both from 2005). (According to loc.cit.: “Because the protection of the outer IP addresses in IPsec AH is inherently incompatible with NAT, the IPsec AH was left out of the scope of this protocol specification.”) For NAT-Traversal, three ports must be open on the NAT device:
NAT-T encapsulates both IKE and ESP traffic within UDP( source and destination) port 4500:
This encapsulating UDP packet is NOT encrypted; therefore the NAT device can change its addresses and process the message.
The VPN can connect:
A VPN connection commonly uses one of the following two protocols underneath:
either TCP (Transmission Control Protocol):
or UDP (User, or, jocular, Unreliable, Datagram Protocol): Packets are sent without any confirmation; that is, no guarantee that sent data arrived correctly. This duty is shifted to applications that use the protocol (for example, VOIP applications). The faster and preferable option for connecting a VPN, if the above two restrictions that TCP circumvents do not apply.
UDP: Internet Protocol used for fast transport of data across a TCP-IP network due to the absence of reliability checking;
A Port is a software, rather than a hardware
concept. It is a number (between 0 and 65535)
that stands for a data channel into and out of a computer in a network.
The header of a packet of the Transmission Control Protocol (TCP) (or
the User Datagram Protocol, UDP) contains a source and destination port
number. This TCP (or UDP) packet is encapsulated in an Internet Protocol
(IP) packet, whose IP header contains a source and destination IP
address. An Internet Socket can be defined as the pair
of an IP Address and TCP Port.
Port numbers fall into three distinct ranges:
0 – 1023);1024 – 49151),
and49152 –
65535).Some Well-Known (or Dedicated) ports are dedicated to certain protocols, for example, port 80 usually to the HTTP protocol for retrieving web pages. Their numbers are assigned by the Internet Assigned Numbers Authority (IANA). They can be used only by system processes (or by privileged users’ such as root).
| port | protocol |
|---|---|
| 13/tcp | Daytime Protocol |
| 17/tcp | Quote of the Day |
| 21/tcp | FTP: The file transfer protocol - control |
| 22/tcp | SSH: Secure logins, file transfers (scp, sftp) and port forwarding |
| 23/tcp | Telnet, insecure text communications |
| 25/tcp | SMTP: Simple Mail Transfer Protocol (E-mail) |
| 53/tcp | DNS: Domain Name System |
| 53/udp | DNS: Domain Name System |
| 79/tcp | Finger |
| 80/tcp | HTTP: HyperText Transfer Protocol (WWW) |
| 88/tcp | Kerberos Authenticating agent |
| 110/tcp | POP3: Post Office Protocol (E-mail) |
| 119/tcp | NNTP: used for usenet newsgroups |
| 139/tcp | NetBIOS |
| 143/tcp | IMAP4: Internet Message Access Protocol (E-mail) |
| 443/tcp | HTTPS: used for securely transferring web pages |
| port | protocol |
|---|---|
| 21/tcp | FTP: The file transfer protocol - control |
| 22/tcp | SSH: Secure logins, file transfers (scp, sftp) and port forwarding |
| 25/tcp | SMTP: Simple Mail Transfer Protocol (E-mail) |
| 53/tcp | DNS: Domain Name System |
| 53/udp | DNS: Domain Name System |
| 80/tcp | HTTP: HyperText Transfer Protocol (WWW) |
| 143/tcp | IMAP4: Internet Message Access Protocol (E-mail) |
| 443/tcp | HTTPS: used for securely transferring web pages |
Internet Protocol Security (IPsec) is a stack of protocols that secures Internet Protocol (IP) communications by authenticating (and optionally encrypting) each packet (over public and insecure networks). It is mainly used for VPNs and is, at least in the business market, the most established protocol. IPsec was developed by the Internet Engineering Task Force (IETF) as an integral part of IP version 6. Recommend official sources to gain an overview of the entire IPsec protocol suite are the documentation roadmap RFC2411 and its security architecture RFC4301. (See also Friedl (2005) for an illustrated informal guide.)
IPsec as a VPN offers Interoperability with IP protocols: It operates at the Internet Layer of the Internet Protocol Suite (comparable to network layer in the OSI model). Other common Internet security protocols, such as Secure Sockets Layer (SSL), Transport Layer Security (TLS) and Secure Shell (SSH), operate on a higher application layer protocol. This makes IPsec more flexible, because applications can ignore IPsec in contrast to the other higher-layer protocols.
Tunnel mode is usually used between gateways through the Internet and connects two networks between two gateways. The end devices themselves connected via the two networks do not have to support IPsec. The security of the connection is only provided on the partial route between the two gateways. Tunnel mode encrypts the whole IP packet. A new external IP header is used. The IP addresses of the two communication end points are located in the inner protected IP header.
Tunnel mode: encrypts the whole IP packet.
Transport mode is usually used when the final destination is not a gateway. It uses an additional IPsec header between the IP header and the transported data. It is less secure than tunnel mode as it only encrypts the data portion but leaves the original IP addresses as plaintext.
Tunnel mode: encrypts the data portion but leaves the original IP addresses as plaintext.
IPSEC essentially consists of the Internet Key Exchange (IKE) and Encapsulated Security Payload (ESP) protocol. IKE is the technical implementation of the Internet Security Association and Key Management Protocol (ISAKMP) framework. IKE uses UDP at port 500 for the initial key exchange (IKE) and port 50 for the IPSEC encrypted data. ESP (for NAT traversal) uses UDP port 4500 and TCP port 10 000.
Establishes a common secret key
The cryptographic Internet Security Association and Key Management Protocol (ISAKMP) defined by RFC 2408 describes the key exchange protocol, but does not specify the used cryptography. IKE implements the ISAKMP and establishes a mutual secret key by the Diffie-Hell. IKEv2 is a tunneling protocol that is standardized in RFC 7296 (a joint project between Cisco and Microsoft) and it stands for Internet Key Exchange version 2 (IKEv2). It extends IKE and simplifies configuration and connection establishment. The first version of IKE came out in 1998 and version 2 in December 2005.
To be used with VPNs for maximum security, IKEv2 is paired with IPSec. In comparison to other VPN protocols, the single most important benefit of IKEv2 is its ability to reconnect quickly after VPN connection loss. In particular useful on mobile devices, which usually support IKEv2 (natively).
Internet Key Exchange (IKE): uses UDP at port 500 for the initial key exchange, either manually or automatically by certificates
Provides authentication and protection against replay attacks, but no confidentiality. That is, the user data is not encrypted and can therefore be read by anyone. AH protects the invariant parts of an IP datagram: IP header fields that can be changed by routers on their way through an IP network (for example, TTL) are not considered. If routers with activated Network Address Translation (NAT) are passed on the way through the network, then they change the actually invariant parts of an IP datagram, and authentication is therefore no longer possible. Thus NAT and AH are incompatible by design! Instead, ESP is possible, which essentially superseded AH.
Authentication Header (AH): Provides authenticity, but no confidentiality. Essentially superseded by ESP.
ESP (specified in RFC 3948) encrypts all critical information by encapsulating the entire inner TCP/UDP data packet into an ESP header. An IP protocol like TCP and UDP (OSI Network Layer 3), but without port information like TCP/UDP (OSI Transport Layer 4). Unlike Authentication Header (AH), ESP in transport mode does not provide authenticity for the entire IP packet. In Tunnel Mode, where the entire original IP packet is encapsulated and a new packet header added, ESP protects the whole inner IP packet (including the inner header) while the outer header remains unprotected. It provides:
Encapsulated Security Payload (ESP): encrypts all critical information by encapsulating the entire inner TCP/UDP data packet. An IP protocol like TCP and UDP (OSI Network Layer 3), but without port information like TCP/UDP (OSI Transport Layer 4).
IPsec, thanks to its long development history:
However:
Other options are:
An alternative to IPsec is SSL-VPN that builds on SSL/TLS. Whereas IPSec provides network security as a whole, SSL VPN’s only to certain applications and for remote client access.
OpenVPN is a popular unstandardized open-source VPN protocol over the UDP or TCP protocol that uses TLS for key exchange (and OpenSSL for encryption). It supports dynamically assigned IP addresses behind NAT gateways. Using TLS, it is incompatible with IPSec. It is implemented as software which is
In comparison to IPsec:
WireGuard: a minimalist and modern open-source VPN software built into Linux kernel 5.5 (and above).
Wireguard is a minimalist and modern open-source VPN protocol over the UDP protocol implemented in software. WireGuard
is simple, user-friendly and easy to set up,
is secure thanks to latest cryptographic algorithms and best practices; for example, the key exchange uses perfect forward secrecy (that is, every connection session uses a different key pair).
has short source code (initially around 4000 lines in comparison to hundreds of thousands in, say, OpenVPN).
is relatively young, and thus lacks all the years of security audits established VPNs such as IPsec and OpenVPN have gone through.
only allows UDP on IPv4 or IPv6; TCP support is missing. In contrast, OpenVPN, also offers TCP and thus works in an environment where only TCP/80 and TCP/443 are open, such as public Wi-Fi networks. (Third party or anyway additional code is required to use TCP as the tunneling protocol); (DSVPN is a Dead Simple VPN in the minimalist spirit of WireGuard that was made to address this common use case of a client on an untrusted and restricted network connecting to a VPN server.)
does not verify the identity of the server by certificates. For authentication, Wireguard uses a public/private key pair (whereas, for example, OpenVPN (by default) a username with password). For example, to generate the key-pair, the command:
wg genkey | tee privatekey | wg pubkey > publickeycreates the two files publickey and
privatekey (which should be generated on the device that
requires the private key and then the public key distributed, rather
than the other way round.)
cannot manage IP addresses dynamically; the client’s addresses are permanently assigned and visible on the VPN server: The client needs to be permanently assigned an IP address that is uniquely linked to its key on each VPN server. A user’s IP address could be found out by an attacker (say by WebRTC) and then matched with records from a VPN provider (obtained, say, by theft or legal enforcement). For this reason, many providers refrain from using WireGuard for fear of their customers’ privacy (despite zero-log policies).
To securely use a shared VPN, one must trust its operator and users: though most users are well-behaved citizens, a single one possibly not, so that, say under law enforcement, all network traffic eventually could be scrutinized. To set up one’s own VPN, there are several software options:
SoftEther (“Software Ethernet”) VPN is free and
open-source,
OpenVPN is complex; see for example the overview Archwiki (2020). The
shell script openvpn-install at Nyr (2019) simplifies the setup of a VPN
server on a UNIX operating system for the inexperienced user. It starts
from entering the following one-liner in her terminal:
wget https://git.io/vpn -O openvpn-install.sh && bash openvpn-install.shAlgo is a set of Ansible scripts (a tool to automatize
the set up of computers on a network) that simplifies the setup of an
(IPSEC) VPN. It uses only the software necessary and the most secure
protocols available, works with common hosting services, and does not
require client software on most devices.
Transport Layer Security (TLS) and its predecessor, Secure Sockets Layer (SSL), are cryptographic transport protocols that provide authentication, confidentiality and authenticity for data sent over a reliable transport protocol, typically TCP. It encrypts data in both directions and (almost always) guarantees the identity of the server and (optionally) the client. Originally developed by the Netscape Corporation, it is now supported by all the major browsers and the most common security protocol used on the World Wide Web.
TLS/SSL: cryptographic transport protocols that provide authentication, confidentiality, and authenticity for data transmitted over a reliable transport, typically TCP
For an application programmer, TLS (and SSL) provide a protocol that can be accessed almost like plain TCP. For a user, they establish a safe channel over the Internet to allow the user’s private information, such as credit card or banking account numbers, to be safely transmitted via certificates, public and symmetric keys (indicated by a small padlock on the web browser’s address bar).
TLS sits on top of the transport layer (in the OSI reference-model, layer 4) as it requires reliable data transfer. Therefore, it sits at least at layer 4 (and thus, in the IP reference-model, at layer 4).
It deems sensible to situate it at:
Authentication and encryption is established by X.509 certificate. Principally, a file that contains the name, address and public key of the web site and is signed by a certificate authority. These are organized hierarchically and pass trust from the upper to the lower level; those at the top, which are trusted unconditionally, are called root authorities. In practice, this unconditional trust is achieved by the deployment of their self-signed certificates, for example, as part of an Internet browser installation.
X.509 certificate: a file, signed by a certificate authority, that contains the name, address and public key of the Web site.
The signature of a X.509 certificate is the encryption
by the private key of the hash of the concatenation
where
V = version X.509,SN = serial number of the certificate,AI = algorithm identifier number,CA = name of the certifying authority,TA = validity interval time of the certificate,A = name of subject, andKA = subject’s public key.The scheme of hierarchical authorities was created to establish trust through machines and has the comfort that the key exchange can be automated. However, trust is a human matter, and has as its Achilles’ heel the (absolute) trust in (root) authority. The user must:
trust that the key public belongs to the authority;
trust that the private key to authority is not compromised;
trust that authority does not abuse its power thus granted; for example, by charging high prices. To compare,
Let's Encrypt
provides free certificates and has a budget of 3 Million $,GlobalSign charges $224 a yer per
certificate.trust that the authority will do its duty, for example, in the verification of the identity of the third party by the authority. To this end, each root certifier is subject to periodic audits (which leads us to ask whether the same goes for the auditors, the auditors’ auditors, … ?!).
The level of security is reflected by the shape of the padlock in the browser’s address bar Whereas Let’s Encrypt’s certificates only verify via e-mail the ownership of the domain, companies offer (GlobalSign at $469.50) an Extended Validation (EV) certificate that verifies the identity of the owner:
common certificate, like a free one from
Let's Encrypt, the verification is completely automated
without any personal off-line verification. To obtain the certificate,
access to the domain suffices. For example, this can be proved to the
authority by uploading a file received by it.Extended Validation (EV) certificate
the verification of the site owner is done in person.
To prevent DNS Hijacking, for example, to make sure the site
belongs to the intended owner (for example, to avoid confusion between
deutschebank.de and deutschbank.de), it is
important to verify in the address bar the padlock indicates an
extended certificate. for example, the browsers
Firefox and Chrome indicated it by the green
color of the entity name before 2020, but more recent versions
(
respectively 77 ) abandoned it V. (2019) because it reportedly took up
valuable screen estate, especially on mobile devices, and distracted the
user.
By the common certificate, the user is only ensured to communicate with the owner of the domain, but not that it belongs to the company or organization that the site appears to represent. Thus, the common certificate,
DNS Cache poisoning, where the
name address (for example, deutschebank.de) is resolved to
the numeric IP address of another server.MITM attack by a user’s confusion between the address and
the (legal) person.The heart of the TSL/SSL protocol is the handshake that sets up the session encryption, whose steps are given. The definitive reference is RFC:5426; a splendid step-by-step illustration
The following steps are the first steps between a client and the server, for example, an e-commerce site, to establish an encrypted connection (for example, to receive credit card data from the client).
The “Hello” between client and server, where the client proposes, and the server chooses, a cryptographic package; that is, the set of cryptographic algorithms,
MD5, SHA, …),
andRSA, …),RSA, ECC, …),AES, Camellia, RS4, …). Often,
the server does not choose the most secure symmetric algorithm, but the
most economical one.For example, the cryptographic package
TLS_RSA_WITH_3DES_EDE_CBC_SHA (identification code
0x00 0x0a) uses
RSA to authenticate and exchange the keys,3DES in CBC mode to encrypt the
connection, andSHA as a cryptographic hash.Besides this, both, the user and the server create a nonce, that is, a number used once, for a single use, which contains
4 bytes to set the time, and20 random bytes,to avoid a replay attack; that is, the re-use of authentications for other sessions.
The server identifies and authenticates itself by its X.509 certificate, which contains (principally):
the server address and its public key (that uses the asymmetric algorithm initially agreed on to exchange the symmetric key),
to authenticate, the name of a certificate authority (such as a
root certificate authority, for example, VeriSign), and its
digital signature (that uses the cryptographic hash and asymmetric
algorithm initially agreed on); that is, the encipherment, by the
authority’s private key, of the cryptographic hash
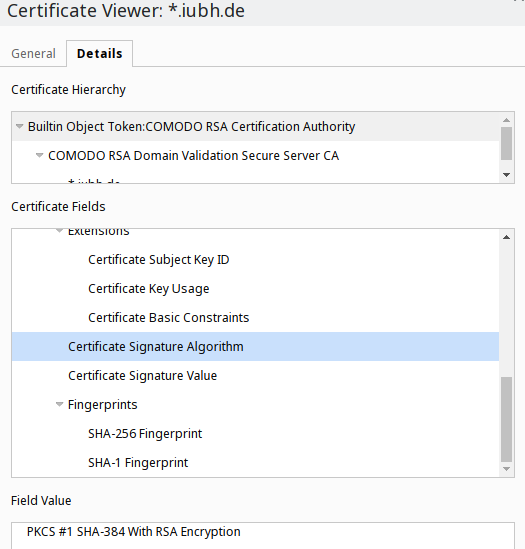
For example, in the picture, the server is
www.iubh.de
Comodo RSA Domain Validation Secure Server CA intermediate
authorityComodo RSA Certification Authority,The client looks for the (root) certificate authority’s public key indicated on the certificate (and which is usually included in the browser), and uses it to decipher this digital signature. If the result is the expected hash (that is, that of the server address and its public key), then
Since the client (or, more accurately, its browser) trusts the root authorities unconditionally, at this point it is certain the public key truly belongs to the target server. (Optionally, at this point also the client authenticates itself by a certificate).
The client
48 bytes,The server
The client and server calculate the secret
(master secret), a number of 48 bytes, by a
function PRF,
master_secret = PRF(pre_master_secret, ClientHello.random + ServerHello.random)which uses as input
the pre-secret, and
the “nonces”, that were communicated during the “Hello”,
The client and the server derive four symmetric keys (for the
algorithm initially agreed on, for example, if it is AES,
each one 16 bytes long) from the secret. (That each side
has a different key is due to the best practice of using a different key
for each different use.) Namely:
client_write_MAC_secret,server_write_MAC_secret,client_write_key, andserver_write_key.Among these,
Observation: Optionally,
In addition to the mandatory authentication of the server (by a certificate), the client authenticates itself in the same way (by a certificate);
the server and the client exchange an ephemeral asymmetric key to send the symmetric key:
RSA algorithm (and is used to sign the ephemeral encryption
keys),ECC or
ElGamal).This ensures that a compromised private key of the signing key stored on the server does not compromise the exchanged session data.
RSA) to authenticate
and exchange the keys,AES to encrypt the
connection, andSHA256.Most Internet protocols, among them the ones for e-mailing, such as
POP3, IMAP and SMTP, initially
ignored security concerns and exchanged all data in plain text. Since
then, various approaches have surged to encrypt the data
TLS), more convenient, that is, easier to set up and
use;S/MIME or
OpenPGP), more secure: In end-to-end encryption, the data
is encrypted and decrypted at the end points, the recipient’s and
sender’s computers. Thus, an e-mail sent with end-to-end encryption is
unreadable to the mail servers (hosted by, say, Hotmail or
Gmail). Thus, for example, no third party (such as a
sensitive organization that hosts its own e-mail server) can scan e-mail
for malware; instead, it has to be done by the user(’s computer) after
decryption.However, end-to-end protocols require additional effort and still only provide partial protection:
The most common e-mail protocol for encryption during transport is STARTTLS. It is a TLS (formerly SSL) layer over the plaintext protocol (such as IMAP4 and POP3 defined in RFC2595) that allows e-mail servers to encrypt all exchanged data between the servers as well as between servers and clients. However, certificate verification is optional, because a failure of verification is considered less harm than failure of e-mail delivery. That is, most e-mail is delivered over TLS provides only opportunistic encryption.
STARTTLS: a TLS layer over the plaintext protocol that allows e-mail servers to encrypt all exchanged data between all relay servers.
Use of STARTTLS is independent of whether the e-mail’s
contents are encrypted or not. An eavesdropper cannot see the encrypted
e-mail contents, but it is decrypted and thus visible at each
intermediate e-mail relay. This is, the encryption takes place between
the servers, but not between the sender and the recipient. This is
convenient
However, because every relay can easily read or modify the e-mail, this is also insecure. If the receiving organization is considered a threat, then end-to-end encryption is necessary.
Transport layer encryption using STARTTLS must be set up by the receiving organization. This is typically straightforward; a valid certificate must be obtained and STARTTLS must be enabled on the receiving organization’s e-mail server. To prevent downgrade attacks organizations can send their domain to the ‘STARTTLS Policy List’
The Secure Multipurpose Internet Mail Extension (S/MIME) is a protocol that standardizes public key encryption and signing of e-mail encapsulated in MIME using certificates emitted by an authority. S/MIME’s IETF specification in Ramsdell (2009) enhances the Privacy Enhanced Mail (PEM) specifications of the 90s. Initially RSA public-key encryption was used, but since RFC:5753 (from 2010) ECC as well.
S/MIME: An e-mail encryption protocol that uses certificate authorities to establish trust for key distribution.
Most e-mail clients, such as Microsoft Outlook or
Mozilla Thunderbird, support S/MIME secure e-mail. Before
use, one must install an individual key certificate, that is, before
installing it:
After successful verification, the certification authority creates a certificate of the key by signing it with its private signature key.
Depending on the security class 1, 2 or 3, the certification authority checks more or less strictly whether the public key truly belongs to the applicant:
(Class 1) S/MIME certificates, which are mostly intended for private
use, are available for free: For example, from CAcert, a
non-commercial, community-operated CA. However, a common e-mail client
or web browser does not recognize it as a trusted certificate authority.
Thus, by default, bare of a manual installation of its certificate, a
user who receives an e-mail with an S/MIME certificate
signed by CAcert is warned that the origin of the
certificate is unverified. Companies, which, in contrast to CAcert, are
also recognized as trustworthy by common software:
GlobalSign as a Free Trial PersonalSign 1 Certificate
(valid for one month),Secorio S/MIME [3] (valid for one month; uses
certificates from Comodo), orWISeKey as free secure email eID (valid for one year).
(Attention: the “private-key” is generated on the server and is
therefore known to the provider!)The web of trust is based on propagation of personal trust. It has the principal advantage that is a peer-to-peer system, that is, it is independent of any particular third party such as an authority. However, as its major inconvenience, it needs personal maintenance. It also
reveals information such as
does not scale well; that is, the amount of storage for the web of trust of the whole world would be immense. For the level of authentication it provides, it makes no sense at these scales.
The web is as safe as its least safe node; that is, a (easily) compromised node puts all its connecting nodes at risk.
For example, so-called “key-sign parties” commonly gather strangers who sign their keys to each other. This is the opposite of what trust means: It should only be passed on when we know the owner of the key we sign!
A compromised key can be used to sign any other key on the web of
trust. For example, imagine that Alice wants to encrypt a message to
Bob. Let Charles’s key be compromised by a
man-in-the-middle.
The man-in-the-middle
Alice, by the web of trust,
Even if this fraud is discovered by others (the idea of the web of trust is that it is impossible to fool everyone), some damage has already been done.
In practice, instead of the web of trust, it is more feasible to
establish trust through another impersonal channel (by exchanging the
fingerprints of public keys), for example, by post, by phone, by a
messenger like WhatsApp, …
OpenPGP: An e-mail encryption protocol that uses the web of trust for key distribution.
Since trust is a personal matter, the automatic unconditional trust
of the user placed into root certificate authorities (principally
companies) is unsatisfactory. The alternative OpenPGP
protocol relies on the web of trust to communicate by e-mail. Still, few
people use it: Most regard the (concrete personal) effort needed for
maintaining the keys (which inherently requires the user’s estimate of
her trust in the keys) disproportionately large for the (abstract)
benefit (of greater privacy and security) received. Unfortunately,
conceivably because so few people use OpenPGP, the
usability of dedicated programs has improved little in recent years:
OpenPGP key management should be easier:
OpenPGP protocol. Even if
the user loses (in part) control over trust, gaining comfort helps to
spread this protocol to laymen. The security they offer is
Opportunistic Security as explained in Dukhovni (2014): as long as nobody’s interested,
it is safe; Otherwise, it is vulnerable to a man-in-the-middle
attack.The OpenPGP protocol has its conceptual
shortcomings:
The Off-the-Record e-mail protocol specified in
Borisov, Goldberg,
and Brewer (2004) was designed to address the
shortcomings of OpenPGP. It offers:
Off-the-Record: e-mail protocol that provides Repudiability and Perfect Forward Secrecy.
The recent program opmsg at Krahmer (2019) (as an alternative to
GPG presented below) implements this protocol (partially).
It
opmsg terminology) for each correspondent,We present some programs that use the OpenPGP protocol,
such as
GPG to create keys and
(de)encrypt and sign/authenticate for them,Enigmail for the e-mail client
Thunderbird, andMailvelope for the Internet browsers
Firefox and Chrome to encrypt e-mails on web interfaces like
gmail.com and Hotmail.com.Gnu Privacy Guard, for short GnuPG or
GPG, was written to offer open and free
cryptographic methods to the public. It is a command-line program
for
It underlies the cryptographic functionality of many cryptographic
applications with a graphical user interface (GUI
applications). It is installed on most Linux distributions, and is under
macOS and Microsoft Windows. The development
of GPG by the German Werner Koch started in
1997 (and hasn’t stopped to this day) to have a free
alternative to the commercial e-mail encryption program
Pretty Good Privacy (= PGP) by Phil
Zimmermann.
1999, in 2000 the German
Federal Ministry of Economics and Technology sponsored a port to
Microsoft Windows, and2015, he was running out of resources and asked for
financial help, which he received amply Angwin (2015).
Among the many functions, GPG creates a pair of keys for
you, one public and the other private, where it lets you choose
RSA),The public key is intended for disclosure, to encrypt and check signatures. The private key is stored and protected by a password, to decrypt and sign.
The Enigmail program is an extension to the graphic
e-mail program Thunderbird that adds to it the functions
to
The user can access these functions by buttons in
Thunderbird itself; to implement these, it uses
GnuPG underneath. According to Snipes (2019), the Thunderbird 78 release,
planned for summer 2020, has the functionality for e-mail encryption and
digital signatures using the OpenPGP standard built-in and replaces the
Enigmail add-on, and therefore the dependency on GnuPG,
whose installation was a hassle for beginners.
Mailvelope is an extension for the browsers
Firefox and Chrome, developed by the
Mailvelope GmbH, which adds encryption and decryption
functions to the web interface of common e-mail providers such as
Gmail, Hotmail.com, and
Yahoo!
For example, enciphering and deciphering messages (using the
OpenPGP standard), files on your hard drive, and send
encrypted e-mail attachments. Mailvelope is open source and
based on OpenPGP.js, an OpenPGP library for
JavaScript. It is comfortable, but comfort comes at the
expense of security (and thus it is safer to use an e-mail client, such
as Thunderbird); for example, it is potentially vulnerable
to Cross-Site Scripting (XSS) attacks, where one site
accesses local data stored for another
with the user’s consensus, the e-mail provider has access to the user’s secret keys to synchronize them between devices (which is comfortable, but also risky).
the Javascript language in which the extension is
written is not the most appropriate for secure encryption; among others,
is susceptible to the following flaws:
XSS)
attacks, where one site accesses local data stored for another;Programs such as
AutoCrypt for Thunderbird and
prettyeasyprivacy for Outlook,Delta-Chat for Android,offer as described in Dukhovni (2014) only Opportunistic
Security: Protection against passive, but not active,
eavesdroppers; that is, the encryption only protects the user as long as
nobody is interested in her! Such a program, precisely because of the
lack of verification of the owner of the private key that corresponds to
the public key, is vulnerable to the man-in-the-middle
(MITM) attack in which the attacker interposes himself
between the two communicating parties. For example, it is perfectly
possible to use someone else’s name on an e-mail or
WhatsApp account. Therefore, encryption of the
communication only prevents it from being read by a third party, but
does not guarantee the other correspondent’s identity. To avoid this
attack, one must personally (or via another channel, for example, via
telephone) check the fingerprint (a cryptographic check sum) of the
other correspondent’s public key. Tedious, but unavoidable.
The program Autocrypt automates the exchange of public
keys and is supported by many e-mail clients, such as the graphical
e-mail client Thunderbird, the command-line client
Mutt or K-9 Mail for Android. It was initiated
by the European Union in response to the revelations by Edward Snowden
(Krekel, McKelvey, and
Lefherz (2018)).
Autocrypt automatically adds a line to the e-mail header
(normally invisible to the user) that contains the sender’s certificate
(name, e-mail address and reference to her public key). This information
is then automatically used by the recipient to encrypt her response.
(Additionally, it is encrypted by her own key for secure local storage.)
Therefore, all but the first e-mail exchanged between two
Autocrypt users are encrypted.

Instead of the automatic usage of the Alice’s public key by the
recipient Bob, more secure would be if Bob’s e-mail
insisted on checking Alice’s fingerprint through another channel (for
example, by telephone).
Another program to automatically send encrypted e-mails as
Autocrypt that supports commercial programs such as the
e-mail client Microsoft Outlook is prettyeasyprivacy. Founded by a
private initiative, it is a graphical interface for
GPG(4Win) that it installs and uses underneath for its
cryptographic functions,. A convenient feature for us humans is to use
so-called safe words instead of hexadecimal encoding to
verify the fingerprint of a public key, that is,
40 hex characters like
72F0 5CA5 0D2B BA4D 8F86 E14C 38AA E0EB,ocean contamination goose arenas survey.The application Delta-Chat (available under Linux,
Windows, macOS, Android and iOS) https://delta.chat/ uses the user’s e-mail account to
send automatically encrypted instant messages. It uses the same open
protocol as e-mail (IMAP, which is old with many
deficiencies, but is the established time-tested standard with a large
ecosystem). Therefore:
WhatsApp),Delta Chat as they still receive the messages sent in
Delta-Chat by e-mail.
This interoperability, for example, that a hotmail.com
user can communicate with another gmail.com user, is called
federation. The dependency on a single company brings the
following problems:
the user has to place all her trust in this company, about which she usually knows little on a personal level, where trust is established, for example:
the company is as a single point of failure, for example:
WhatsApp has occasionally happened, for example, in Brazil
http://www.dw.com/pt-br/whatsapp-volta-a-ser-suspenso-no-brasil/a-19413134
and continues to happen in China).That being said, the meta-data between the e-mail servers is still unencrypted. However, the user can consciously choose a mail server which does not exploit the users’ meta-data; for example, she sets up her own server or pays a monthly fee to a trusted provider.
The messenger Conversations
proposes a modern XMPP protocol that uses less meta-data
than the IMAP e-mail protocol. (Apparently the messenger Signal uses less meta-data than
Conversations, but almost all servers are maintained by the
vendor Open Whisper Systems itself, in contrast to
Conversations. After all, the only secure solution is to
run one’s own server!). It is a secure messenger, but unfortunately
little established; for example, there are many IMAP mail
servers, but few use XMPP.
The Domain Name System (DNS) is a distributed database analogous to a phone book of the Internet.
DNS: database of all Internet domain names distributed on hierarchically organized servers over the Internet.
DNS translates human-friendly alphabetic Internet domain address,
such as https://www.ongel.de, to a computer-friendly numeric IP address,
such as 194.6.193.105 (as can be found out by the Unix
command-line program nslookup). This Internet-domain
address takes the form of
For example, ongel.de has the domain name
ongel and the TLD de. Domain and TLD names
were initially registered and governed by Inter Network Information
Center (InterNIC), a cooperation between the US government and the
company Network Solutions Inc, which managed the registration and
maintenance of .com, .net, and
.org top-level domain names. In 1998 the US government
liberalized the process of registration and set up the ICANN that
administers Registrar companies for registering domains; for example,
the company VeriSign registers domains ending in the TLDs
.com and .net. Generic Top-Level-Domains
(gTLD) such as .com are more strictly controlled by the
ICANN than country-code Top-Level-Domains (ccTLD) such as
de as a concession to state sovereignty. (An alternative
Network Information Center is OpenNIC, which adds its own
top-level domains such as .pirate, .geek or
.libre to those from ICANN and operates free DNS
servers.)
A Fully Qualified Domain Name (FQDN) (such as
www.ongel.de) is a unique (worldwide) name (to address an
IP address) on the Internet and which can be freely chosen under the
rules determined by the Internet Corporation for Assigned Names and
Numbers (ICANN):
.de),www) can be added to a FQDN (such
as ongel.de) by prepending it with a dot (to result in,
say, www.ongel.de). Common subdomain labels are, for
example, www. for Web servers and mail.,
smtp., pop3. and imap. for
(outgoing and incoming) mail servers.ongel) may
contain at most 63 characters and the entire FQDN (such as
www.ongel.de) at most 255 characters.The FQDNs are put in correspondence with the IP address by the entries of name servers.
Fully Qualified Domain Name (FQDN): a unique (worldwide) name (to address an IP address) on the Internet
The labels of a FQDNs are represented as nodes of a tree. A FQDN is then a path of the tree:
de).ongel)www) …
DNS is defined in Mockapetris (1987) and uses the UDP or TCP protocol on Port 53. DNS servers use a set of databases distributed on servers over the Internet that are organized hierarchically.
DNS zone: the subset of the DNS hierarchy which is described by a zone file, a list of entries that map a FQDN name to its IP address.
A DNS zone is the subset, often a single domain (say
ongel.de), of the DNS hierarchy which is described by a
zone (text) file; a list of entries
called resource records (RRs) that map a FQDN name to
its IP address. The zone file format, as originally specified for the
Berkeley Internet Name Domain (BIND) software, is used by most DNS
server software. It contains
usually the ORIGIN keyword, that specifies the
starting point for the zone in the DNS hierarchy; (If omitted, then the
starting point is inferred by the server software from the reference to
the zone file in its server configuration.)
exactly one Start-of-Authority RR (SOA-RR), usually at the beginning of the file, that contains
admin@ns.ongel.de),ns.ongel.de), andat least one name-server RR, usually following the SOA-RR, for the authoritative name servers for this zone (among which figures at least the primary authoritative name server);
possibly one or more NS-RR that delegates the DNS resolution of a
subdomain to another name server (say resolution of all subdomains below
www.ongel.de is delegated to
ns.www.ongel.de).
root server: is the name server that resolves all FQDNs of a top-level domain (TLD)
A root name server, or root server for short, is the
name server that resolves all FQDNs of a top-level domain (TLD) such as
.com.
The concept of a domain name server came around in the 80s: As the
size of computer networks grew, it became increasingly difficult for
humans to keep track of which machine corresponded to which number.
Before DNS, names were resolved into IP addresses by a list (such as
/etc/hosts on Unix operating systems) that had to be
available on every computer on the Internet. Changes were first made
manually on a master server and then downloaded by the clients. As the
number of IP subscribers increased, this procedure became increasingly
unwieldy. In 1983 Paul Mockapetris specified the Domain Name System
(DNS), the first DNS software JEEVES was developed and the first three
DNS root servers went into operation.
In the early 80s, the DNS software BIND for UNIX
(Berkeley Internet Name Domain) was developed at the University of
Berkeley, whose version 4 became the worldwide standard. Further
development of the software was taken over, for a short time, by the
company DEC and then by Vixie Enterprises led by Paul Vixie. Starting
with version 4.9.3, BIND became the responsibility of the
non-profit organization ISC (Internet Systems/Software
Consortium). Version 8 was completed in 1997. In 1999 ISC
commissioned Nominum Inc. to develop version 9, which has been the
standard since 2007 and forms the backbone of the worldwide Domain Name
System.
DNSsec: DNSsec protocol to authenticate the resolutions of a domain name to an IP address.
The DNSsec protocol allows the client to authenticate its requested
resolution of a domain name to an IP address. For this, the resolution
is signed on registration by the DNS server responsible for the zone
file. This provides authenticity of the resolution, but neither
confidentiality (that is, the request and its resolution are
unencrypted) nor authentication of the DNS server. To this end, further
secure DNS protocols, such as DNScrypt,
DNS-over-TLS and DNS-over-HTTPS have been
devised and will be discussed below.
The DNSSEC protocol as extension to the DNS protocol was standardized in RFC 25352 in March 1999. However, this version proved in practice unsuitable due to elaborate key management. The roll-out of DNSSEC was delayed till the completely rewritten version RFC 40331, RFC 40343, and RFC 40354 was published in 2005, which obsoleted RFC 25352. In May 2010 DNSSEC was introduced on all 13 root servers; in July the root zone key was published. In the meantime, 90% of the top-level domains are signed with DNSSEC and marked as signed in the root zone. A few are still testing DNSSEC without an entry in the root zone. The distribution of DNSSEC at domain level for some TLDs is now 50% or more. On average, about 10 % of domains validate.
The chain of trust along the hierarchy of the DNS architecture ensures that the public key in the resolver’s DNSKEY record in the zone file is correct by automatic successive signature verification up to the trust anchor. The trust anchor is the first key in the chain of trust, the key upon which the chain resides, the public key associated with the root name server (which is entered manually). To establish trust along the chain, every server below must know this key. See Sandia Corporation (2014) for a tool that visually analyses the DNSSEC authentication chain for a domain name and its resolution path in the DNS namespace.
Currently, the private DNSSEC key for the root zone is managed at two US locations. Critics accuse ICANN, after it had chosen the American company Verisign as its exclusive signing partner, of putting the independence of the Internet at risk through exclusive DNSSEC key management in the USA.
trust anchor the key upon which a trust chain resides.
DNSSEC defines four levels of trust in a record:
DNSSEC is a protocol that extends DNS. It therefore includes all entries (Resource Records; RRs) of a DNSSEC packet. RFC 4034 specifies the addition of the four RRs: DNSKEY , RRSIG , NSEC and DS.
DNSKEY The DNSKEY record is passes a public key between the resolver and the name server. This public key is the one associated with the private key with which the authority server will sign hashes of RRSET records. The resolver will use the public key in the DNSKEY record to authenticate the message of the authority server by verifying its signature.
RRSIG record contains the signer’s name and the signature of the record sent by the authority server; the signature that the resolver will later verify. There is one RRSIG record for each zone record in the signed zone file.
The NSEC record is used for proof of non-existence. It contains the name of the next authority domain or point of delegation for the request and the records that exist for that name.
Next Domain Name field: Contains the name of the next authority domain for the request according to the RRsets order relationship. For the name following the last RRset, the name of the parent field is returned.
DNSSEC authenticates each resource record (RR) by a digital signature, as follows: Owner of a RR is the primary authoritative name server as defined in the Start-of-Authority RR (SOA-RR) entry of the zone file.
If no server matches the request, then DNSSEC proves that no such RR exists uses a new type of record that sends the name of the first (in alphabetic order) existing domain.
Zone Signing Key (ZSK) respectively Key Signing Key (KSK): the key to sign the (hashed) RRs respectively to sign the ZSK.
The more encrypted data, the more information to infer the keys used to encrypt the data: Because of the large amount of data encrypted by the key to sign the (hashed) RRs (the so-called Zone Signing Key; ZSK), this “working” key must be renewed regularly. To avoid network administrators having to renew the ZSKs too often, the Key Signing Key (KSK) has been introduced, which is longer and has to be renewed less regularly. While the public keys are stored in DNSKEY-RRs, the KSK and ZSK private keys are stored offline. In more detail:
Virtual hosting makes it possible to host multiple DNS names on a
single (web) server, in particular, on the same IP address. This reduces
server maintenance and the number of IP addresses (which are scarce in
IPv4; every IP address assignments must be justified to the
regional Internet registry).
Virtual hosting: allows multiple DNS names to be hosted on a single server (usually a web server) on the same IP address.
For example, a server receives requests for the domains,
www.ongel.de, www.ongel.org and
www.ongel.net, which resolve all to the same IP address.
But for www.ongel.de, the server sends the html file
/var/www/user/de/site/index.html, while he responds
accordingly for the top level domains .org and
.net. Likewise, two subdomains of the same domain can be
hosted together: for example, mail.ongel.de and
ftp.ongel.de.
The distinction which domain on the server was requested is made at the application level: For example, the requested domain is sent, always unencrypted,
SMTP protocol, during the SMTP
handshake.HTTP protocol, by the HTTP header
field Host sent by the client as is obligatory since
HTTP/1.1 (which is commonplace today, but whose inclusion
cannot be enforced by the server).HTTPS protocol, for a suitable assignment of
certificates to domains, both, client and server, must support Server
Name Indication (SNI):The biggest gripe with name-based virtual hosting is that of multiple
secure websites running TLS/SSL. In
HTTPS, the TLS handshake happens before the
server has received the HTTP headers, and it can therefore
not send the certificate for the requested domain name. Therefore, the
HTTPS server can only serve one domain on a given IP
address.
The TLS protocol extension Server Name Indication
(SNI) defined in RFC 6066, addresses this problem by
sending the domain name during the TLS handshake. This
allows the server to choose the virtual domain earlier and thus send the
certificate corresponding to the DNS name asked for. Therefore, with
SNI-aware clients, a single IP address can be used to serve a group of
domains without a common certificate.
SNI: extension of TLS that sends the domain name during the
TLShandshake.
By 2013, most browsers and TLS libraries implemented SNI, but about 20% of users still had software that was incompatible with SNI 5. However, by 2019, this number had fallen below 3%.
Observation. The host name is not sent encrypted in
SNI. (ESNI, Encrypted Server Name Indication, as drafted in Rescorla et al. (2018), is
supposed to solve this security hole.) SSL/TLS with SNI
reveals more information than SSL/TLS without SNI, since the server
certificate then transmitted also contains the domain(s) for which it
was issued in plain text. If instead the certificate were valid for
multiple domains, then the full requested host name would not be
transmitted.
A reverse DNS lookup (or resolution), rDNS, queries the Domain Name System (DNS) to determine the domain name associated with an IP address. That is, it is the reverse of the usual DNS lookup of an IP address from a domain name. It uses (so-called PTR, pointer) records through the reverse DNS database of the Internet rooted in the .arpa top-level domain. Although the informational RFC 1912 (Section 2.1) recommends that “for every IP address, there should be a matching (PTR) record”, not all IP addresses have a reverse entry, for example, when a web server hosts many virtual domains.
In DNSsec authenticates DNS replies by a signature from the authoritative DNS server on which the domain name was registered; not necessarily the DNS server that answered the DNS request. DNSsec thus offers authenticity of the DNS entries but:
Secure DNS protocols
The three principal contenders for encrypted and authenticated DNS queries and replies are:
DNSCrypt protocol (supported by Cisco OpenDNS, among
others),DNS-over-TLS (or DoT), DNS resolution over
TLS (supported by Cloudflare, Google, and OpenDNS), andDNS-over-HTTPS (or DoH), DNS resolution
over HTTPS (supported by Cloudflare and Google).The DNS server SecureDNS.eu, operated by Dutchman Rick
Lahaye, supports all three of these: DNSCrypt,
DNS-over-TLS and DNS-over-HTTPS.
Neither Windows, macOS nor
Linux support encrypted DNS queries by default at the time
of writing. However, Android 9, supports DoT. Firefox
supports encrypted DNS queries by DoH and Google, at the
time of writing, is testing DoH over Chrome.
DNSCrypt has less backing from the big companies.
Because all the other sent metadata in particular usually include the requested DNS, encrypting DNS queries mainly shifts it from one party (the DNS server without encryption) to another (the DNS server with encryption). Since most requests on the Internet leak the domain name (for example, reverse DNS lookup or by protocol headers, see below), the merit of secure DNS queries lies less in the protection against eavesdropping, but more in the authentication of the DNS server. However, authentication (of the requested domain) is usually already provided by TLS. On the downside, centralization of all DNS queries (away from the ISPs) to the DNS provider permits their bundled processing: While the data between the client and the server is encrypted during transport, it is decrypted at each end.
The domain name can be inferred from the IP address by reverse DNS lookup: The Internet service provider (ISP), who connects the client to her destination by its IP address, can still (to a good measure) figure out the client’s DNS destination by Reverse DNS lookups: (Though this is not completely reliable, for example, the web hosting service can lodge many domains at the same IP address by virtual hosts or move a domain from one IP address to another.) Thus, not only the DNS server can track the visited websites, but the ISP as well. Therefore, for privacy it is preferable to use the ISP’s DNS server, because the ISP already implicitly has the information passed to the DNS server.
The domain name is sent as plaintext:
HTTP protocol, by the HTTP header
field Host sent by the client as is obligatory since
HTTP/1.1 (which is commonplace today, but whose inclusion
cannot be enforced by the server).HTTPS protocol, for a suitable assignment of
certificates to domains, both, client and server, must support Server
Name Indication (SNI) that sends the DNS name of the domain
as part of the TLS handshake (so that the server can send
the certificate corresponding to the requested DNS name on an IP with
various domains.)STARTTLS.In DNSCrypt the client, instead of relying on
X.509 certificates emitted by trusted certificate
authorities as found in web browsers, has to explicitly trust a public
signing key used to verify a set of certificates (retrieved using
conventional DNS queries). These certificates contain short-term public
keys used for key exchange, as well as an identifier of the used cipher
suite. Clients should generate a new key for every query; servers should
rotate short-term key pairs every 24 hours.
DNSCrypt: unstandardized secure DNS protocol without trusted certificate authorities.
According to DNSCrypt Team (2019a),
the DNSCrypt protocol sits over the TCP
(mandatory) and UDP (optionally) transport protocols. The protocol has
been around since 2013, but is not standardized (say, in an
RFC).
The client sends a (non-authenticated) DNS query to a DNSCrypt resolver, which encodes the certificate versions supported by the client, as well as a public identifier of the provider requested by the client.
The resolver responds with a set of signed certificates, that must be verified by the client using a previously distributed public key, the provider public key. Each certificate includes a validity period, a serial number, a version that defines a key exchange mechanism, an authenticated encryption algorithm and its parameters, as well as a short-term public key, known as the resolver public key. (A resolver can offer multiple algorithms and resolver public keys.)
The client picks a certificate (that with the highest serial number among the valid ones that match a supported protocol version) and encrypts by the resolver public key to send an encrypted query, which includes a (magic) number (to identify the chosen certificate) and the client’s public key.
The resolver
Advantages:
DNSCrypt’s is among all secure DNS protocol the one
closest to normal DNS.UDP port 443, address are resolved
relatively fast and little likely to be blocked by a firewall.Disadvantages: - DNSCrypt does not rely on trusted
certificate authorities, but the client has to trust a chosen public
signing key. That signing key is used to verify certificates that are
retrieved via conventional (unencrypted) DNS requests and used for key
exchange - While many DNS services use DNSCrypt (such as CleanBrowsing,
which blocks adult content domains, and Cisco OpenDNS, which blocks
malicious domains), recent DNS services (including Google, Cloudflare,
and Quad9) opted instead for DNS over TLS and DNS over HTTPS.
DNS-over-HTTPS was specified in RFC8484 and uses HTTPS to be indistinguishable from any other HTTPS traffic and is thus practically never blocked. Firefox has added support for DoH through the DNS servers of Cloudflare. (Google plans on testing DOH with Chrome.)
DNS-over-HTTPS: DNS-lookup protocol that uses HTTPS.
DNS-over-TLS, thanks to the IETF standardization in RFC7858, is the
most widely supported in software; For example, Android 9 supports DoT.
DoT clients authenticate the service they connect to using Simple Public
Key Infrastructure (SPKI) which is a joint effort via the
IETF to simplify traditional X.509 PKI and a supported standard of
establishing trust.
DNS-over-TLS: DNS-lookup protocol that uses TLS.
DoT is plain DNS traffic within a TLS connection using a dedicated
port 853 (and occasionally on port 443). That is, up to the encryption
by TLS, it is the same as DNS over TCP/IP instead of UDP.
Since TLS is the encryption protocol used to secure almost all other
Internet services, the technology is well understood and constantly
improved.
See DNSCrypt
Team (2019b) for a comparison (to
DNSCrypt).
Advantages:
Disadvantages:
Advantages:
Disadvantages:
Advantages:
Disadvantages:
Which port uses the DNS protocol? DNS is defined
in Mockapetris (1987) and uses the
UDP or TCP protocol on Port.
Which data reveals the server visited by the user other than her DNS request?
HTTPS protocol, the Server Name Indication
(SNI), andHTTP protocol, the header field
Host.List three protocols to securely look up domain names:
The protocols that standardize communication on the Internet can be stacked in to layers: the Open Systems Interconnection (OSI) reference-model with seven layers (more of a theoretical abstraction), and the Internet Protocol Suite with four layers (the practical standard). The layers are ordered according to how much structure the processed data has, the higher the layer, the closer to the user’s applications. The two most important Internet protocols (and those that were defined first) are the Transmission Control Protocol (TCP), and the Internet Protocol (IP), that specify how data should be formatted, addressed, transmitted, routed and received at the destination.
A virtual private network (VPN) is a private network made up of two or more closed (spatially separate) networks connected via an open network (such as the Internet). The IPsec VPN uses one of two Modes: The transport mode establishes point-to-point communication between two end points, while the tunnel mode connects two networks via two gateways. In IPSEC tunnel mode, IP packets are encapsulated (tunneled) in other IP packets.
Transport Layer Security (TLS) Protocol and its predecessor, Secure
Sockets Layer (SSL), are cryptographic transport protocols that provide
authentication, confidentiality, and authenticity for data transmitted
over a reliable transport, typically TCP. Authentication and encryption
is established by X.509 certificate. Principally, a file
that contains the name, address and public key of the web site and is
signed by a certificate authority. These are organized hierarchically
and pass trust from the upper to the lower level; those at the top,
which are trusted unconditionally, are called root authorities.
E-mail is encrypted: either only during transport (for
example, TLS), more convenient, that is, easier to set up
and use; from end-to-end (for example, S/MIME or
OpenPGP), more secure: In end-to-end encryption, the data
is encrypted and decrypted at the end points, the recipient’s and
sender’s computers. Thus, e-mail sent with end-to-end encryption is
unreadable to the mail servers.
The Domain Name System (DNS) is a distributed database on the Internet that resolves human-readable domain names into machine-readable IP addresses. DNS offers neither privacy as all data exchanged is unencrypted, nor trust, as the DNS server does not need to authenticate. DNSsec offers authenticity by signing all DNS records, whereas more recent secure DNS protocols encrypt all exchanged data and authenticate the DNS server to a client.
How many layers does the OSI model have?
4510How many layers does the TCP/IP reference model have?
357Which protocol is not part of the IPsec protocol family?
Which kind of (cryptographic) algorithm is not agreed on during the TLS handshake?
RSA,AES,SHA256,CBC.Which security feature is neither part of the S/MIME
nor OpenPGP protocol?
Read the carefully crafted illustrated guides on IPsec
Friedl (2005)
respectively TLS Driscoll (2019).
Read Dukhovni (2014) on opportunistic security.
On completion of this chapter, you will have learned …
where, why and how random numbers in cryptography are generated; in particular, the distinction between physical and pseudo-random number generation.
how to ensure long-term security (in 10 to 20 years of time, for example, of health data) by
best practices for using cryptography in application development, by
to conform to legal regulatory requirements by using encryption for data protection, of utmost importance, for example, in health care,
to be aware of government trap doors and security holes potentially kept secret by intelligence agencies
Even though the presented algorithms are secure in theory, in practice a lot may go wrong when implementing cryptography; thus, as a software developer, caution must be taken and best practices adopted:
Most importantly, use what is vetted by the test of time; for
example, as a software developer, to use (open-source) software
libraries that implement cryptographic functions such as encryption,
decryption, signing and verification. Besides the cryptographic
algorithms, critical is the implementation of the random number
generator, which is notorious for exploits: As we saw, in
ECC, elliptic curve cryptography, if the same ephemeral key
, usually randomly generated, for signing is used twice to sign
different documents by the same private signature key, then the
ephemeral becomes known and reveals the secret signing key.
Even when well-known time-proven cryptographic open-source libraries, for example, OpenSSL can have security holes, such as the Heartbleed bug contributed by a PhD-student at the Fachhochschule Münster, that made common web servers reveal on request currently processed secret data, such as passwords or server keys. Even though quickly fixed, the question remains if in the meanwhile intelligence agencies exploit these, on top of back doors built into cryptographic software (usually on the behest of government agencies).
Even best cryptographic practice does not stop Moore’s law that predicts a doubling of the computing power every 18 months that progressively weakens keys. Besides continual progress, there may be technological leaps, such as the quantum computer, which would break many common asymmetric ciphers such as Diffie-Hellman, RSA and Elliptic Curve Cryptography and more involved alternatives have been found.
Cryptography requires random numbers to generate
True randomness is critical for the generation of keys but less so and can be dispensable nonces (where sometimes a key is used as a nonce, see below), for which uniqueness is can be sufficient. For example,
GnuPG strong random number generator (for
cryptographic keys) builds a pool of 600 entropy (physical disorder)
bytes and hashes these by SHA-1.GnuPG nonce generator adds 20 bytes containing the
process ID number (PID) and the time in seconds and 8 bytes taken at
random from a strong random number generator, and hashes these with
SHA-1.A secret (that is, a secret sequence of bits, or, equivalently, a secret number) often must be generated by the computer; for example,
DSA (Digital Signature Algorithm) and its analogue over
elliptic curves, ECDSA, which the El Gamal signature
algorithm underlies, generate an ephemeral key pair for every plaintext
to be signed.For secrecy, it is necessary that the output of the generation is unpredictable; since the generation algorithm is usually known, its input must be unpredictable. This excludes, for example, using as input computer times or a number of a known sequence.
For example, if the secret ephemeral key used by the signature
algorithms DSA (Digital Signature Algorithm) and its
analogue over elliptic curves, ECDSA is known, then the
signee’s permanent secret key can be inferred; that is, an attacker can
forge the signee’s signatures!
In particular, if two of the same signee’s ephemeral public keys used
for different documents coincide, then the secret ephemeral key used by
either of these signature algorithms can be inferred. (For example, the
standard (Java) library for the generation of a random number on Android
generated repetitive random numbers, thus allowing to forge signatures
of users of an Android Bitcoin app, see Ducklin (2013))
Therefore, in this case, the generated number must be unique.
While true randomness of numbers are critical for security-sensitive applications and can be generated using hardware random number generators, pseudorandom numbers are often sufficient for less confidential ones, for example, for (probabilistic) experimental simulations such as the Monte Carlo method.
A Pseudorandom Number-Generator produces sequences of numbers which
appear independent of each other, that is, which satisfy statistical
tests for randomness (which require careful mathematical analysis such
as the BigCrush Test Suite L’Ecuyer and Simard (2007)), but are produced by a definite
mathematical procedure, However, this apparent randomness is sufficient
for most purposes The random number generators provided by most software
libraries are pseudorandom. See “List of Random Number Generators —
Wikipedia, the Free Encyclopedia” (2020) for a
list of such pseudo-generators. An ancient influential and simple such
is the Linear congruential generator, which for a multiplier
,
offset
and modulus
produces the sequence
inductively given by
Its successor that use linear feedback
shift registers replace arithmetic in
by that in the binary polynomial ring
. An efficient one that passes the BigCrush Test Suite is, among others,
Xorshift+ 128 , an adaption (to pass the test suite) of
Xorshift that iteratively multiplies a nonzero initial
-bit string by an invertible matrix of order
.
Other generator that pass the test suite are the hash function
SHA-1 and the symmetric algorithm AES (with
initial values).
A hardware random number generator is a computer device that
generates random numbers from a physical process which is theoretically
completely unpredictable, for example, thermal noise, voltage
fluctuations in a diode circuit or, quantum optics (which can provide
instant randomness). In Unix operating system, randomness is gathered
from the devices /dev/random and /dev/urandom.
GnuPG, in absence of these, uses process statistics, but also supports
the hardware RNGs inside the Padlock engine of VIA (Centaur) CPUs and
x86 CPUs with the RDRAND instruction.
List at least three uses of random numbers to generate keys:
How to ensure that data encrypted today will still be secure in the decades to come? This is in particular relevant for certain long-lived applications, for example, health data. In practice, the security of a cipher, and thus the recommended key sizes, relies foremost
One has to take into account
Moreover, preventive measures can be taken by diversifying the keys used for encryption so that a single compromised key compromises as little ciphertext as possible: Perfect Forward Security generates a new key (pair) for every new session (that is, exchange of ciphertexts).
World’s fastest supercomputer, IBM’s Summit (taking up 520 square meters in the Oak Ridge National Laboratory, Tennessee, USA) has around petaflops, that is, floating point operations per second. The number of flops needed to check a key depends for example, on whether the plaintext is known or not, but can be very optimistically assumed to be . Therefore, Summit can check approximately keys per second; thus, a year having seconds, approximately keys a year.
To counter the increasing computing power, one prudently applies Moore’s Law that stipulates that computing power doubles every other year. Therefore, every twenty years computing power increases by a factor . Therefore, to ensure that in, say, sixty years, a key not surely be found during a yearlong search by world’s fastest supercomputer at least key combinations have to be used.
For a key of bit length , the number of all possible keys is . If , then there are are possible key combinations. While this number is sufficient for now, the probability for the key to be found during a yearlong search by world’s fastest supercomputer being around , the projected fastest super computer in twenty years will likely find it in half a year. Instead, to be safe against worlds fastest yearlong supercomputing efforts in 40 years, a minimal key length of is recommended.
For the symmetric algorithm AES , the fastest known
algorithm currently is exhaustive key-search, to try out all possible
keys, whose complexity (= the number of operations) is
. The minimal AES key length is
bits; that is, there are are
possible key combinations. Therefore the chance that world’s fastest
supercomputer in say, sixty years, finds the secret key is around
, a millionth percent. We conclude that the minimal AES key length is
safe against brute-force attacks for the years to come.
In contrast to single-key cryptography whose cryptanalysis exploits statistical patterns, by its reliance on computationally difficult mathematical problems (that is, whose runtime grows exponentially in the bit-length of the input), the cryptanalysis of two-key cryptography is that of computational mathematics: to find an algorithm that quickly computes the solutions of the difficult mathematical problem. According to Arjen K. Lenstra (2006), for the classic asymmetric algorithms,
RSA, orthe fastest algorithm is the General Number Field Sieve
whose number of operations, roughly, for a large number of input bits
,
putting
,
is
where
To compare this to the number of
operations
required for exhaustive key-search of a key of bit length
,
we put
,
equate both numbers of operations, and obtain
which must be solved numerically for
;
for example, for
,
that is,
we find
,
that is,
,
to satisfy
;
therefore
and
.
That is, at least as much computational effort is needed for finding a
private
bit long key for RSA and Diffie-Hellman by the
General Number Field Sieve as for finding a secret
bit long key (say, for AES ) by exhaustive key-search.
For the logarithm over a finite elliptic curve, the fastest algorithm
today is the generic baby step, giant step algorithm (or, slightly
faster, Pollard’s
-algorithm) that complexity is roughly
.
Therefore, for the computational effort for finding a private key of bit
length
for Elliptic Curve Cryptography to be comparable to that for finding a
secret key of bit length
(say, for AES ) by exhaustive key-search, the key length
must double, that is
.
By these formulas, we can calculate that
RSA or
Diffie-Hellman key must be at least
bits to be as secure as that of an AES key of
bits, andECC key must be at least
bits to be as secure as that of an AES key of
bits.These key sizes are therefore sufficient for the decades to come, assuming that no faster algorithm than those known is discovered to solve the underlying mathematical problem.
Quantum researchers hope to build computers that harnessing a phenomenon known as superposition where a quantum system is in many possible states before a measurement “collapses” the system into a single state:
A classical computer stores information in bits; each bit is either on or off. A quantum computer uses qubits, which can be “entangled”, in-between on and off so that it can carry out multiple calculations at the same time and whose final output depends on the interferences generated by them. However, actually building a useful quantum computer has proved difficult:
The properties measured on one of one particle depend on the operations carried out on all the others: If a particle can take two states (denoted 0 and 1), a system of two particles can take for example states 00 or 11, or even a superposition of these states: For example, each of the two particles, considered in isolation, is measured randomly as a 0 or a 1, but the particles are “twins”, that is the measurement of a state of one of the two particles forces the other particle one into the same state. The violation of a statistical inequality (predicted by John Bell in 1964 and verified experimentally, among others, by Alain Aspect in 1982) proves that this is a characteristic of the particles and not due to a (hidden) link.
A physical quantity in quantum mechanics is called observable and is usually in a superimposed state; only in special (so-called eigen)states it has a uniquely determined (so-called eigen)value. In general, the eigenstate is the result of applying an observable to a (superimposed) state and choosing an eigenvalue.
Formally, a (superimposed) state is a complex unit vector, that is, a vector of length one with complex entries and an observable is a (self-adjoint) operator on the vector space of all states. Because is self-adjoint, there is a basis such that for real ; each is an eigenstate and its eigenvalue.
An eigenstate is an eigenvector of and interpreted as the possible outcome of a measurement for a given observable; A general state is a linear combination of eigenstates. The complex coefficient of is called the probability amplitude of and its absolute value in is the probability of the measurement of .
Whereas a digital computer processes bits, that can be in one of two states, 0 or 1, a quantum computer processes quantum bits (qubits) whose states superpose:
The basis states are those probability amplitudes that have a single nonzero entry of value , of which there are . The state whose entry of value is at in is denoted by .
Example. A single qubit superimposed between and is denoted by such that , the probability amplitude of two qubits together superimposed between , , and is denoted by with .
Each elementary operation on the state space is then described by a (unitary) matrix of columns (orthogonal to each other): each column is the probability amplitude obtained by applying the operation to the corresponding basis state.
A quantum computer can solve many classical problems faster than a classical computer. For example,
to find an item among an unordered list of items on a classical computer, on average operations are needed, and one cannot do better than that. However, a quantum algorithm exists that achieves this in only about operations!
Simon’s problem: given a function that transforms -bit strings into -bit strings, find the nonzero bit-string such that for all -bit strings . To solve Simon’s problem on a classical computer, one searches for a collision that needs around evaluations of . However, a quantum algorithm exists that achieves this in only about operations!
Shor’s Algorithm Peter Shor of AT&T in 1994 in his article “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer” gave a quantum algorithm that factors a number (for ) in operations and memory units. Instead, on a classical computer, solving the factoring, discrete logarithm (DLP), and elliptic curve discrete logarithm (ECDLP) problems takes subexponential time, around operations. Therefore, given a sufficiently large quantum computer, current public key encryption schemes are easily broken.
Shor’s algorithm requires a quantum computer of around 8000 entangled qubits to factorize a 4096-bit RSA key, and is therefore not imminent.
Therefore, given a sufficiently large quantum computer, current public key encryption schemes are easily broken. (In compensation, quantum mechanical effects offer a new method of secure communication known as quantum encryption.) RSA, for example, uses a public key which is the product of two large prime numbers. One way to crack RSA encryption is by factoring , but with classical algorithms, factoring becomes increasingly time-consuming as grows large; no classical algorithm that factors in operations for some is known.
However, while a quantum computer can solve many classical problems faster than a classical computer, not all of them; the problems solved are all subexponential, that is, exponential in a root of the bit length of the input (for example, in the cube root for prime factorization and discrete logarithm), whereas genuinely exponential problems, in particular problems that are NP-hard (such as finding the closest vector to a lattice) are conjectured to remain hard even on a quantum computer.
This cipher was published in 1997 by Oded Goldreich, Shafi Goldwasser, and Shai Halevi, and uses a trapdoor one-way function that relies on the closest vector problem which is NP-hard. Though this specific algorithm was later cryptanalyzed by Phong, it illustrates the principles on which modern withstanding lattice based ciphers stand, such as NTRU: Given any basis of a lattice, it is easy to generate a vector close to a lattice point by adding a small error vector to the latter. However, to return from this shifted vector to the original lattice point, a particular type of basis is needed.
The private key consists of
The public key is the basis of the lattice .
If a message (a vector of integers) and a public key are given, then to encrypt the plaintext :
If a ciphertext and the private key consisting of a lattice basis and unimodular matrix are given, then to decrypt the ciphertext :
Code-based post-quantum ciphers are asymmetric ciphers that are based on error correcting codes to transmit bits over a noisy channel: To avoid that Alice sends, say , but Bob receives , a simple solution would be that Alice repeats each bit thrice, , and Bobs takes for each group of three the bit that appears most often: For example, would be decoded to . However, this encoding scheme is limited to one erroneous bit in each group of three bits. Instead, a linear code multiplies the bit vector with a matrix , that is, computes . For any number of erroneous bits , the matrix can be chosen such that at most erroneous bits in are correctable (to ).
The first encryption scheme based on linear error-correcting codes was developed by McEliece in 1978 and is still unbroken; due to the (secure) public key size of around kilobytes, it was shrugged off before the advent of quantum computing. More exactly, the algorithm uses the error-correcting code Goppa codes. Goppa codes are easy to decode, but distinguishing them from a general linear code is known to be NP-hard. The Post Quantum Cryptography Study Group installed by the European Commission has recommended this type of cryptography against quantum computers.
The private key are three matrices, an error correction matrix , and invertible matrices and ; and the public key is = that can correct error bits.
To encrypt: compute for an error term containing errors.
To decrypt:
Hash-based cryptography is based on the security of cryptographic hash functions rather than on the hardness of mathematical problems. Lamport showed how to derive a one-time signature scheme from any one-way function, such as a cryptographic hash function, and Merkle improved on it by the Winternitz one-time signature (WOTS) in Merkle (1990); “one-time”, because a private key can only be used securely once:
Let be the private key; fix an integer . The public key is , the -fold nested application of the hash function to . The signature of a message, given by an integer , with the private key is the -fold nested application of the hash function to , that is, . The signature is checked by the equality
This simple scheme is insecure. For example, signatures can be forged: From the signature of , one derives the signature of by Therefore, one must sign not only by , but also by a different key. Still, this scheme
Modern hash-based signatures are more sophisticated than
WOTS; however, they can still either only securely sign one
message for each key, or, such as SPHINCS, sign a limited
number of messages but produce large signatures.
Perfect Forward Secrecy means that after the
correspondents exchanged their (permanent) public keys and established
mutual trust,
This way, even if the correspondence was eavesdropped and recorded,
it cannot be deciphered later on; in particular, it cannot be deciphered
by obtaining a correspondent’s private key. For example, the
TLS protocol, which encrypts much communication over the
Internet, supports since version 1.2 Perfect Forward Secrecy: More
specifically, in the handshake between client and server,
TLS protocol
superfluous.)The mutual secret key can be established, for example, by the
DHE (Diffie-Hellman Ephemeral) or ECDHE
(Elliptic Curve Diffie-Hellman Ephemeral) protocol This key is then used
as input to generate a secret symmetric key, for example, for the AES
encryption algorithm.
List three types of algorithms considered secure in the advent of quantum computers:
Risk analysis measures the likelihood that an organization’s security will be breached (for example, an intruder exploiting network vulnerabilities) and calculates the inflicted damages from such a breach, be they material (such as data privacy violation) or immaterial (such as a reputation loss). The risk is often measured as a financial risk and countered similar to insuring against threats such as theft. Risk analysis
assesses the threats (by an intruder or company’s insider) to the company’s computer network. According to the CSI/FBI Survey, the biggest ones are, in this order
assesses the values of the company’s assets, consisting of:
the company’s vulnerability, that is, where, how and how a security breach could happen.
prescribes preventive measures, for example,
builds plans to quickly recover from an exploit.
The First Rule of Cryptography: Don’t implement cryptography yourself in production code. Instead, leave it to the experts and use a proven library that withstood the test of time under the scrutiny of cryptanalysts rather than a home-made one:
AES and RSA are recommended. If instead a new
one is used, no safety can be assured. In particular, it is a bad idea
to design a proper new cryptographic algorithm.Libsodium (or the widely-used OpenSSL), are
recommended.Programmers often confuse the encryption and authentication. While encryption ensures confidentiality, authentication ensures integrity. When they have to be done separately: Encrypt then authenticate (that is, compute a MAC, Message Authentication Code). Verify the MAC before decryption. A priori, there are three options for authenticated encryption:
Authenticate and Encrypt Together: The sender computes a MAC of the plaintext, encrypts the plaintext, and then appends the MAC to the ciphertext. This is what SSH does.
In this order, the MAC (over plaintext) leaks information about the plaintext; for example, whether two messages have the same plaintext (by their identical MACs).
First Authenticate then Encrypt: The sender computes a MAC of the plaintext, then encrypts both the plaintext and the MAC. This is what SSL does.
First Encrypt then Authenticate: The sender encrypts the plaintext, then appends a MAC of the ciphertext. This is what IPsec does.
This way, one can verify the MAC and discard texts without decryption; thus
Only Encrypt-then-Authenticate is provably secure in theory, that is,
secure against IND-CCA (indistinguishability of ciphertext
for chosen ciphertexts), that is, an attacker can ask for any
pair of ciphertexts to be deciphered (excluding the ciphertext in
question), and still cannot distinguish which one among two plaintexts
corresponds to the ciphertext:
The oracle creates a secret key.
The attacker asks for the decryption of any ciphertext (except the one in question), and creates two plaintexts and of equal size.
The oracle
The attacker asks for the decryption of any ciphertext (except the one in question), and
chooses a bit in .
Example. Bleichenbacher’s attack on
PKCS#1 from 1998 is not secure against IND-CCA.
A cipher is secure against IND-CPA
(indistinguishability of the ciphertext for chosen plaintexts),
if no attacker can distinguish which one of two plaintexts, that he
selected before, corresponds to the ciphertext that he receives
afterwards. Bellare and Namprempre showed in 2000 for a symmetric cipher
that if
IND-CPA, andthen the cipher with “Encrypt-then-MAC” resists an “IND-CCA” attack.
That neither Encrypt-and-Authenticate nor Autenticate-then-Encrypt aren’t secure in theory, but Encrypt-then-Authenticate is, neither means in practice that the former two are insecure, nor that the latter is secure. However, there have been a number of vulnerabilities for the former two, while none for the latter: For example,
Therefore, it is best to use a library that takes care of authenticated encryption as a whole, instead of only offering these functions separately, where one has to be composed correctly oneself; sticking to the golden rule that as much as possible is reused instead of reimplemented:
The AEAD modes (Authenticated Encryption with Associated Data, where Associated Data is whatever must be authenticated but not encrypted) is a modern mode to encrypt and authenticate a message in the same operation, Reliable implementations of AEAD are, for example,
AES-GCM, the Advanced Encryption Standard (a.k.a.
Rijndael cipher) in Galois/Counter Mode, available OpenSSL,
andChaCha20-Poly1305 that combines the
ChaCha20 stream cipher with the Poly1305
Message Authentication Code, available in Libsodium. To store a password, as soon as it is received,
scrypt (that uses, besides the password, a nonce and
iteration count to counter rainbow attacks) or PBKDF2 (but
NOT using a fast hash function, such as MD5, more
vulnerable to rainbow table attacks), andUtmost care must be taken even for less sensitive applications because some users might reuse these passwords for more sensitive ones.
Finally, we recall that Encoding, for example base64
encoding, and Compression, such as Zip compression, aren’t encryption,
as they hardly obfuscate information: Encoding and compression
algorithms are both reversible, keyless transformations of data:
To authenticate and encrypt a message, one should:
Cryptographic functions should be
Which cryptographic hash function should not be used for storing passwords:
bcrypt,scrypt,PBKDF2, orThe General Data Protection Regulation (EU) 2016/679 (GDPR) governs the exposure of personal data, processed and stored by hand or by computers, and applies since 25 May 2018 to all companies in the European Union. Besides the GDPR, other national data protection law may apply, for example, in Germany,
GDPR wages the interests of companies and consumers in the digital age and protects every citizen’s fundamental right of informational autonomy by granting the concerned citizen transparency and ultimate authority in the processing of her own personal data; that is,
Every staff member who processes personal data must be instructed on data secrecy. In general, forwarding personal data to third parties is inadmissible without consent of the concerned person. If exceptionally admission is granted, then data must be encrypted and sent separately for each purpose, so that third parties neither an eavesdrop nor collect data.
What is personal data according to law, for example, the GDPR? General data:
Special data that needs special protection is in general (but also listed similarly, for example, in Paragraph 4, 9 of the GDPR):
ethnic origin, political opinions, religious beliefs, sexual orientation, or syndicate membership
biometric data, such as
gene data,
health records: for example,
Thus, for example, in health care all patient information is strictly confidential by law. For example, in Germany, documents can must be transmitted either encrypted or by fax. Only data necessary for treatment can be collected. The patient data must be confidentially stored and kept confidential by the staff. For example, in Germany the unauthorized disclosure of patient data subject to professional secrecy can be punished, by Section 203 of the Criminal Code (StGB), with a monetary fee or up to one year of prison.
Leaked secret documents show that the American National Security Agency (NSA)
searches for vulnerabilities, such as the Heartbleed
bug; see the section below.
has sabotaged international encryption standards, that is, the algorithms were purposefully weakened for later decryption:
U.S. export regulations lead to the EXPORT ciphers
in SSL used outside the USA, because the stronger ciphers
could not be exported, leading to the so-called FREAK
attack.
GCHQ mandated weak cryptography into the GSM standard to decrypt mobile communication.
In 2004, Greece government officially mandated an interface for wiretapping into telephone talks; though disabled, it was still in the firmware. This was used to eavesdrop on government members.
The Escrowed Encryption Standard (EES) is a chip-based symmetric encryption system developed in the USA in April 1993. The developer of the algorithm is the secret service NSA. It was developed as part of a U.S. government project to provide electronic devices sold to the general public with a security chip. The encryption key was to be provided to the government, which would then be able to eavesdrop on communications if necessary.
The main difference to other encryption methods is that, if necessary, US authorities can get access to the keys used by two users to exchange data. The procedure is specified in such a way that two keys are required for eavesdropping, which are deposited with different authorities and which should only be released at the same time by court order. This official access possibility is not achieved by a built-in back door in the technical sense, but by depositing two partial keys. If the legal conditions are met, the two parts of the key are issued and joined together.
Skipjack was the algorithm used for encryption within the Clipper chip. The chip was designed to resist external modification and allowed the government to access the data in plaintext through a mechanism called Law Enforcement Access Field (LEAF). After the appearance of an attack in 1994 the project was abandoned in 1996. The appearance of software such as PGP, which was not under government control, made the Clipper chip obsolete and the Skipjack algorithms was made public in 1998.
Bullrun (and its British equivalent called
Edgehill) is a secret American program by the NSA
(respectively by the GCHQ) to break the encryption systems used in the
most widespread protocols on the Internet, such as Secure Sockets Layer
(SSL), Virtual Private Networks (VPN) or Voice over IP (VoIP). The
existence of the program was revealed in September 2013 by Edward
Snowden, showing that the agencies have been working on the main
protocols or technologies used in the Internet (HTTPS/SSL, VPN) or 4G
for mobile telephony to intercept and decipher in real time large
Internet data volumes; for example, those circulating on Hotmail, Yahoo,
Facebook and especially Google.
RSA BSAFE is cryptography library in C and
Java by RSA Security; it used to be common
before the RSA patent expired in September 2000. From 2004 to 2013 (till
revealed by Snowden) its (supposedly cryptographically secure) default
pseudorandom number generator Dual_EC_DRBG contained an
alleged kleptographic (allowing for stealing information securely and
subliminally) backdoor from the NSA who held the private key to it, as
part of its secret Bullrun program:
Cryptographers had been aware that Dual_EC_DRBG was a
very poor Pseudo Random Number Generator (PRNG) since shortly after the
specification was posted in 2005, and by 2007, it seemed to be designed
to contain a hidden backdoor usable only by NSA via a secret key. NSA
can potentially have weakened data protection worldwide, in case NSA’s
secret key to the backdoor is stolen. RSA Security did not explain their
choice to continue using Dual_EC_DRBG even after the
defects and potential backdoor were discovered in 2006 and 2007, and has
denied knowingly inserting the backdoor.
The Swiss Crypto AG was an internationally active company in the field of information security. Between 1960 and 1990, at the height of the Cold War, Crypto AG was a leading company for encryption devices and produced for countries for more than 130 countries. The CIA was concerned about being unable to decipher foreign messages and approached European manufacturers, including Crypto AG. The (West) German foreign intelligence service BND and the US intelligence service CIA secretly bought the company in 1970. They arranged for many states to be supplied with machines with weaker encryption that could be decrypted by the BND and CIA (Operation Rubikon).
The company enabled these two services to decipher encrypted messages between the 1960s and 2010, While the suspicious Soviet Union and China were never among Crypto’s clients,the CIA could however learn about some of their exchanges thanks to third countries equipped with tampered devices. For example, the CIA estimates that it could
In February 2020, after evaluating a 280-page dossier, Swiss Radio and Television, ZDF and The Washington Post published a joint investigation which proved that the German BND and the US CIA were the owners of Crypto AG and delivered manipulated ciphering devices to some 130 states as part of Operation Rubikon to eavesdrop on communication.
Heartbleed is a vulnerability in the SSL implementation
OpenSSL, which is used in the popular web servers Apache
and nginx, which are running two-thirds of the web pages at
the time of the bug The Heartbeat allows server and client to
keep a TLS connection alive by sending a message of any content
(payload) from one end to the other, which is then sent back exactly the
same way; to show that the connection is alive:
The RFC 6520 Heartbeat Extension tests TLS/DTLS secure
communication links by allowing a computer at one end of a connection to
send a “Heartbeat Request” message, which consists of a payload,
typically a string, along with the length of that payload as a 16-bit
integer. The receiver must then send the exact same payload back to the
sender.
Versions of OpenSSL subjecet to the Heartbleed bug
allocate a memory buffer for the message to be returned based on the
length field in the request message, regardless of the actual payload
size of that message. Because of this failure to check the appropriate
limits, the returned message consists of the payload, possibly followed
by whatever else is allocated in the memory buffer.
The problem with implementing the TLS heartbeat feature in OpenSSL was that the program does not check how long the received payload is. The attacker can write arbitrary values in the payload_length field provided for this purpose in the header of the payload packet and thus read the memory of the remote peer.
This Hearbleed attack works in both directions; let us
assume that a client is attacking a server:
The attacker sends the server a heartbeat payload that has byte, but claims that it has, for example, kilobytes.
The server writes the attacker’s byte into its memory in a buffer
called pl. Since the actual size of the payload is not
compared, the server assumes the size specified by the attacker
(payload) when the payload is returned.
The server therefore reserves Kilobytes of memory (and a little more for administrative information):
buffer = OPENSSL_malloc(1 + 2 + payload + padding);
bp = buffer;The server then copies the payload size given by the attacker (about Kilobytes) at this place for the response:
memcpy(bp, pl, payload);But the source pl to be copied only has a single byte
from the incoming heartbeat! The following bytes consist of any other
data that the server is currently processing; such as passwords, data of
another user that was just decrypted, or secret keys of the server. The
server then sends the data packet bp to the client, which
can repeat this attack at will.
The tapping leaves hardly any traces on an attacked computer. It is
therefore not certain to what extent the error has been exploited.
However, the news agency Bloomberg reported, citing “two informed
persons”, that the Hearbleed bug was used by the NSA from
the beginning; this was immediately denied by the NSA director: “This
government takes seriously its responsibility to maintain an open,
secure and trustworthy Internet. There is a national interest in
disclosing any such vulnerability as soon as it is discovered.”
When can personal data be collected ?
With a clear purpose and express consent of the person.
Name at least three examples of specially protected personal data:
Many things can go wrong when implementing cryptography; thus, as a software developer, caution must be taken:
AES for symmetric and RSA
for asymmetric cryptography. For example, the cryptocurrency IOTA
implemented its proper ternary cryptography and hash function, which was
quickly unravelled by the Digital Currency Initiative at the MIT.ECC,
elliptic curve cryptography, if the same ephemeral key , usually
randomly generated, for signing is used twice to sign different
documents by the same private signature key, then the ephemeral becomes
known and reveals the secret signing key. For example, the
SecureRandom class of the Java Android Crypto library that
implements cryptographic functions on Android did not properly
initialize the underlying Pseudo Random Number Generator, leading to the
same ephemeral key being used more than once.Even when best cryptographic practices are applied, Moore’s law predicts that continuous technological progress doubles the computing power every 18 months and thus weakens the future security of keys. Therefore, a security margin for long-term security, usually for around twenty years, has to be added. Finally, there may be technological leaps, such as the looming construction of a quantum computer, which would break many common asymmetric ciphers such as Diffie-Hellman, RSA and Elliptic Curve Cryptography and more involved alternatives have been presented.
Which part of a cipher is in practice most susceptible to be exploited?
Which algorithm is secure against a quantum computer?
For at most how many years will projectively an AES -bit key stay secure?
To which AES key size does an RSA key of bits compare?
To which AES key size does an ECC key of bits compare?
On completion of this chapter, you will have learned …
Cryptography secures data exchange on the Internet; for example, it protects the content of a financial transaction, be it between a customer and her bank or users of a cryptocurrency, from eavesdropping (confidentiality) and tampering (authenticity). Because correspondents rarely met in person before, asymmetric cryptography (such as RSA) is the cornerstone of secure data exchange on the Internet that makes possible
However, while cryptography hides the content of the messages, their metadata is not, for example:
In voting cryptography allows the voter to check whether her vote has been correctly tallied. However, to avoid coercion, secrecy of the ballot, that is, anonymity of the vote, must be maximally preserved while the tallying process must stay comprehensible for the average voter. The Scantegrity II voting scheme achieves this by pen and paper probabilistic audits.
The Home Banking Computer Interface is an open protocol specification originally conceived by the two German decentralized saving banks Sparkasse and Volksbanken (and German higher-level associations such as the Bundesverband Deutscher Banken) to unify the online access of the client to her bank by standardizing the homemade software clients and servers. HBCI is the counterpart for the European market of the IFX (Interactive Financial Exchange), OFX (Open Financial Exchange) and SET for the north-american market. HBCI
The Financial Transaction Services (FinTS) specification succeeds HBCI 3.0. It is publicly available on the website of the ZKA (Zentraler Kreditausschuss) and supported by Sparkasse, Volksbanken und Raiffeisenbanken, Commerzbank, Deutsche Bank and more than 2000 other financial institutions. First published as version 3.0 in 2002.
FinTS supports
Starting from version 4.0 from 2004
In 2014 version 4.1 was published that contains improvements gained by years of practical experiences and to adopt:
SEPA (Single Euro Payments Area), a self-regulatory initiative by the European banking sector represented in the European Payments Council to set (technical) standards that uniformize the payment transactions in the European Union (BIC, IBAN, …).
PSD2: The European Union passed in 2015 the revised legal framework Payment Services Directive (PSD2) that all payment service providers of the member states had to respect till 2018,
PSD2 was supplemented in 2017 by technical regulatory standards (2018/389) for (by two-factor) client authentication for secure online payments that had to be adopted till September 2019.
FinTS predefines business transactions codes, but also allows each bank to define their proper codes.
| Code | Name |
|---|---|
| DKPAE | Change PIN online |
| HIISA | Transmission of a public key |
| HKISA | Public key request |
| HKCCS | SEPA (Single European Payments Area) payment |
| HKAUB | foreign bank transfer |
| HKEND | End of dialogue |
FinTS specifies bank parameter data (BPD) and user parameter data (UPD). If the user is represented by an intermediary, then the IPD are the largely identical counterpart (for the intermediary) to the UPD.
BPDs specify all business transactions of the bank and are used to validate the data sent to it; they contain, for example, the supported security procedures, compression procedures and business transactions. Customer software often comes with bank parameter data from common banks.
UPD are sent by the bank and define the user’s access rights for certain accounts and business transactions, and The customer software uses the UPD to check whether the user is authorized to execute one of the business transactions specified in the BPD. For example, the UPD contain the authorizations of the business transactions for each one of the user’s account (for example, to enter payment orders or as a signatory) and other information, such as its currency, a limit …
UPD and IPD are each a subset of the BPD, that is, they can only restrict and detail the BPD, but not extend it.
Client and bank communicate via confirmation codes that are classified by the first digit of the code:
A message is syntactically valid if it obeys the underlying XML schema; if not, they are answered with the confirmation code 9110 for “Unknown structure”.
| Code | Text |
|---|---|
| 0020 | Information received without errors |
| 1040 | BPD no longer current. Current version will follow |
| 1050 | UPD no longer current. Current version will follow |
| 3330 | Keys are already available |
| 9010 | Order rejected |
| 9210 | Language is not supported |
The confirmation codes enable customer software to react automatically to messages from the credit institution; for example, if the response is “wrong institution”, then the software can automatically request the correction of the institution (as part of the IBAN). While the “confirmation text” gives the user plain text information, the confirmation code facilitates customer queries.
FinTS distinguished between the following roles:
Transactions are encrypted
either on the FinTS protocol layer using a key stored
or on the TSL protocol (underlying the HTTPS-Protocol) using PIN/TAN with indexed (iTAN) and mobile (mTAN) transaction numbers, that is, one-time passwords. (iTAN was abandoned in 2019 by the EU payment regulations directive PSD2.)
Using a chip card is the most secure because
If a file is used, then the key must be encrypted by a password chosen by the user and only accessible after manually having entered it.
The PIN/TAN method is more convenient because it does not require a card reader (for example, while travelling).
All asymmetric cryptography uses exclusively the RSA algorithm: The key pairs of the user are to be generated by the customer (from the chip card), and those of the bank are to be generated by the bank; according to the following procedure:
Encryption between client and server is hybrid and uses
RSA for the initial key exchange.
A randomly generated message 32 byte key for the symmetric encryption algorithm:
the current one-time key is encrypted with the public key of the recipient. The length of the one-time key of 256 bits is extended to the modulus length of the public encryption key (2048 bits) by the ZKA padding specified in the crypto-catalogue of the German Banking Industry.
FinTS uses RSA signatures to authenticate transactions (for example, in RAH-9 and RAH-10) and, in RAH-7, to sign transactions by a certificate. The signing key pairs is
An encrypted message is authenticated by signing its plaintext. All messages must be encrypted, with the notable exceptions of those that
For a vote, like every sensitive transaction, for example, a financial transaction,
the voter must be authenticated, and
the vote must be
However, the transaction, the ballot, must be anonymous as well; that is, the receiver cannot know the sender: there is no link to between the voter and her ballot (in particular, that there is no receipt that reveals the voter’s choice). Secrecy of the Ballot guarantees that only the voter herself, but no one else, knows of her choice (with the notable exception of a vote by a physically handicapped person instructing her assistant to give her vote and possibly, though forbidden by law, postal vote).
Integrity is about:
Integrity can only be achieved on the expense of Anonymity, and precautions must be taken to preserve it as much as possible. In an end-to-end auditable (or voter verifiable) voting system, each voter receives an encrypted ID, which she can use to check on a public list whether her choice was likely cast, registered and tallied as intended. The more voters check and errors are committed, the more probable that one of them is detected.
While secrecy can be strengthened by shuffling the assignment of bubbles to candidates on each ballot, the integrity check nevertheless demands a database that assigns each bubble of each ballot to a candidate, and which is owned by the election authorities at some point. Therefore, while integrity can likely be achieved, to break the secrecy of the ballot, it suffices:
To ensure that this assignment between the bubbles of the ballots and candidates is left unaltered during the casting of the ballots, the election authorities commit to it before the election by
cryptographically hashing
publicizing the hashes.
In many countries, the voting process that underlies a democracy should be understandable by everybody (instead of having to trust the computer), thus ruling out the use of cryptography. For example,
Instead, most countries opt for paper ballots that are hand counted. Therefore, instead of using voting machines to cast, register and tally votes, voting procedures such as Scantegrity (see below) are explored that use pen and paper to cast, register and tally votes, but cryptographically identify the ballot with the voter’s choice to ensure authenticity while preserving anonymity.
The Scantegrity voting scheme is an end-to-end voter verifiable voting scheme, that is, each voter receives an ID which she can use to check on a public list whether her choice was likely cast, registered and tallied as intended (and otherwise file a dispute). It was devised by David Chaum et al. in 2008 and supersedes the Punchscan scheme by David Chaum and since then continually evolved into versions I, II to III after trial elections. The paper ballot contains:
The voter can use her ballot to
A database assigns to each bubble of each ballot ID the candidate shown on the ballot. While this assignment could be achieved in a single table
for public auditing of the registration and tally of votes, this assignment is split into two steps and the table kept secret and expanded into three tables:
In table , in each row, the cells whose bubble codes have been revealed on the ballot are revealed. In table , the cells that corresponds to the bubble of a ballot that has been revealed is marked.
The public audit reveals a random half of the assignment between each bubble on a ballot and candidate in table , that is, either the cell in table or the column (and row) in table . While the chance to detect a given manipulated bubble is , the odds to overlook a manipulated bubble among, say, ten manipulated bubbles is below to , that is, the probability is .
If the voter chooses to audit a ballot, then this ballot is
Again, while the chance to detect a given manipulated ballot is , the odds to overlook a manipulated ballot among, say, ten manipulated ballot are below to , that is, the probability is .
As countermeasures to perceived attacks during trial elections with Scantegrity I, while in Scantegrity I the codes of the bubbles are randomly permuted among a set of letters that identify the bubbles, in Scantegrity II (or the basic system): The voter
This way,
the voter cannot ensure to choose a certain bubble code because every ballot contains different bubble codes; therefore she cannot be forced to randomize her vote by choosing a fixed letter.
a voter can prove online and anonymously, without a receipt, that she chose a certain bubble, because:
This avoids
In Scantegrity III, to prevent a human from reading off the information contained in a cast ballot (where all codes given to the voter were detached):
To prevent a voted ballot being turned into an audited or a spoiled ballot, two “authenticated status” codes are added to the ballot and committed to before the election. Each code is printed on the ballot in slow-reacting invisible ink, and individually detachable (for example, using a perforation).
If the voter:
If a voter later on the website,
has voted and finds that
has audited her ballot and finds that
has spoiled her ballot and finds that her ballot is misrepresented (as voted or audited), then, in theory, two additional status codes could be added to detect the misrepresentation; however, in practice it is sufficiently effective to prevent it at the voting booth by destroying all ballot IDs.
List four criteria that an end-to-end voter verifiable voting system should adhere to:
Which election steps in an end-to-end voter verifiable voting system should be verifiable by the voter:
Whether the vote is:
Steganography from Greek steganos, covered, is the art of concealing a message by embedding it within another message so that nobody but the intended recipient knows of the existence of the message. One example is given in The Histories of Herodotus where Histaeus shaved the head of his most trusted slave and punctured a message on his head which became hidden as soon as his hair had grown back.
In contrast, in cryptography the existence of the hidden message itself is not hidden, but only its content (for example, when sending an encrypted e-mail). Thus it makes public, presumably important, information is deliberately being hidden, drawing attention to the fact and possibly pitting interested cryptanalysts against it.
Steganography: the art of concealing a message by embedding it within another message so that nobody but the intended recipient knows of the existence of the message.
In computing, the message is typically hidden in a picture, for example, a compressed JPEG, but also an audio file, say, in the MP3 format, is conceivable. This can be used, for example, to hide, in the picture itself, a copyright notice of the owner of a picture (Coded Anti-Piracy). Because a typical picture file has hundreds of kilobytes, a few bytes can be changed to convey a secret message without noticeable change. The secret information is usually stored in the marginal parts of the image: The simplest picture format is a bitmap, that is, a picture
Because man cannot distinguish more than degrees of each primary color, it suffices to represent each pixel by three bytes.
Least-Significant Bit Substitution: The hidden message, as a stream of bits, can then be stored, for example, in the least significant bit of the eight for each primary color of each pixel: For each byte, as a number between and , the hidden bit is if and only if is odd.
To read the hidden content in a medium, it must be
Steganalysis is the art of detecting and extracting the hidden content in a medium without knowledge
Hidden content can be detected statistically by looking for significant deviations to similar reference data without hidden content. For these deviations to be statistically less significant, the hidden content itself should be statistically random, pattern free; this is for example achieved by encrypting it.
For example, Least-Significant Bit Substitution can be detected by a histogram, a diagram of bars, one for each color in the picture whose height is proportional to the number of pixels of that color. Because bytes that were originally
the heights of each pair of neighboring bars, that is, the frequency of pixels of neighboring colors, will be significantly closer to their mean than in the original picture. Therefore Least-Significant Bit Substitution can be reliably detected when the hidden information makes up less than 1% of the whole picture.
To counter this detection method, Least-Significant Bit Matching, instead of Least-Significant Bit Substitution, adds or subtracts to the byte randomly, instead of exclusively adding to even and subtracting from odd bytes. That is, if the bit of the hidden message is , then, a coin flip decides whether the byte is incremented or decremented (instead of decrementing the byte if it is odd and decrementing it if it is even). Then, like in Least-Significant Bit Substitution, for each byte, as a number between and , the hidden bit is if and only if is odd. However, the heights of each pair of neighboring bars in the histogram are no longer significantly closer to their mean than statistically expected and the problem of detecting .
Kerckhoff’s principle, that an attacker who knows of the steganographic algorithm used to store the hidden information cannot detect it, is however more difficult to achieve in steganography than in cryptography.
The command-line tool Tomb by Denis Roio (aka Jaromil), is a Linux
shell script that encrypt folders by dm-crypt, which is
part of the kernel; the encrypted folders are consequently called Tombs
(whereas dm-crypt calls them containers). These can be
created and integrated into the running system with a few commands on
the command line (which, however, partially need administrative rights).
For highest security, and tomb and its key should not be stored on the
same device. For example, if the tomb is on a PC or notebook, the tomb
could be stored on a USB stick. If however, the key must be stored on
the same device as the tomb, then Tomb offers to hide the key in a JPEG
picture using steganography. This hides the key from unauthorized eyes
and helps remember the key’s location.
Tomb can mount folders that other applications need at runtime, for
example, the mailbox of an e-mail client. To this end, it needs the
package steghide. The key can be hidden in a small JPEG
picture by tomb bury and extracted by
tomb exhume:
tomb bury secret.tomb -k picture.jpgtomb exhume picture.jpg -k secret.keytomb open secret.tomb -k picture.jpgHow does steganography differ from cryptography?
Steganos means cover while crypto means hide in Greek. Steganography covers up a secret message by a plain message while cryptography reversibly scrambles its content.*
Chaum introduced in 1981 Mix-Nets to communicate anonymously on the network by passing the data through relays that can only forward to their nearest neighbors.
Each relay has a public key pair with public keys , …, numbered in the order in which the message travels through them, for the relay after the sender, …, for the relay before the receiver.
To send a message anonymously and confidentially, the receiver sends:
The sender selects the (IP) addresses of the receiver and of each relay , …, .
The sender chooses a random number for each relay (to ensure uniqueness of each message).
The sender
and sends this encrypted data to the first relay.
To receive data anonymously and confidentially, the receiver sends to the sender the following data (which in turn is successively sent to each relay):
The message sent anonymously and confidentially as described above could, for example, be this (encrypted) list of addresses and symmetric keys to receive data anonymously and confidentially.
The receiver selects the (IP) addresses of the sender and of each relay , …, .
The receiver creates symmetric keys for the sender and each relay , …, .
The receiver
and sends this data to the sender.
The sender
The first relay (after the sender)
…
The last relay (before the receiver)
Tor is an implementation of second-generation onion routing to guarantee anonymity on the Internet. It was originally sponsored by the US Naval Research Laboratory, then the Electronic Frontier Foundation (EFF) between late 2004 and 2005.
Onion Routing: A chain in which every node only knows its immediate predecessor and successor, and in which all traffic between both endpoints is indecipherable to every node but the endpoints.
To connect to the network, each client:
The first node in the circuit knows the requested IP address. But from the second node on, the negotiation is done through the already built partial circuit, so that the second node, for example, will only know the IP address of the first node (and eventually of the third node). The packets to be routed are identified by a code (chosen at the time the circuit is built) of the owner of the circuit (the person who built it). Each node of the circuit receives its own private (asymmetric) key encrypted by the public (asymmetric) key dedicated to that node.
Before dispatching a TCP packet to the server, the client encrypts it as many times as there are nodes:
…
At this point, all layers of the onion enclose the TCP packet. The onion is peeled when the client dispatches it to the circuit she has built :
1 and sends it to the second server;2 and sends it to the third server;…
A user on the Tor network can set up her web browser to use a
personal proxy server to access Tor (such as Privoxy); for
example, to connect to ongel.de:
Her web browser sends the HTTP request to
Privoxy;
Privoxy removes the non-anonymous information and
passes the information via SOCKS to the Tor client.
The Tor client
The first node decrypts part of the envelope and forwards the data to the exit node;
This exit node sends the request to
ongel.de.
For the ongel.de website to connect to the user, the
steps are carried out in inverse order.
The most accessible use of the Tor network without advanced computer skills is the Tor Browser:
The Tor Browser is a web browser, available for Linux, Microsoft Windows and Mac that tunes Mozilla Firefox for leave as few traces as possible on the network and the computer:
duckduckgo.com as the default search engine, andNoScript and HTTPS-Everywhere
extensions enabled by default.Tails (The Amnesic Incognito Live System) is an operating system that uses the Tor network by default and designed to leave no trace on the computer being used. It is built to run on removable media (such as USB drives) and is based on the Linux distribution Debian.
How many times does a client encrypt a packet before sending it to the server through ten nodes in a Tor network?
the client encrypts it as many times as there are nodes, that is, ten times
The online banking protocol FinTS standardizes data exchange between the customer and her bank by the XML (Extensible Markup Language) format, and ensures best cryptographic practices such as
The blockchain replaces a third trusted party, the bank, that mediates financial transactions, by a database of entries that successively point to each other. This pointer is a hash of the whole other entry, ensuring the database’s integrity: thus, a change of the entry entails a change of the hash, thus invalidates the pointer, thus the whole chain. Because the hashes must have many leading zeros, finding valid entries, aka mining, demands much computational power and practically turns impossible.
Verifiability of the tallying in an election by cryptography puts additional requirements on its implementation because
While some anonymity has to be put at risk to database breaches by colluding election officials, the Scantegrity II pen-and-paper voting-scheme lets the voter check the tallying of her vote probabilistically by an intermediate private database that connects each ballot to the candidate choices.
While cryptography hides a message by reversibly scrambling it, steganography hides it by embedding in a plaintext message, say, by embedding a secret key inside an image. The most common approach is slightly altering each pixel color according to a set rule; for example, to set the least significant bit (out of eight) to that of the message. If done too naively, for example, as described, than statistical analysis gives away the existence of concealed information; however, if done with care, then it is hardly discovered.
The Tor network achieves anonymous data transfer on the Internet by so-called onion routing, where traffic passes through a chain of nodes in which
Which home banking protocol standard precedes FinTS?
How high is, roundabout in percents, the chance that ten manipulated ballots go undiscovered in the Scantegrity II voting scheme?
What does the Greek word Steganos translate to?
What routing technique does the anonymity of data transfer in the Tor network rest on?
On completion of this chapter, you will have learned the anatomy of the blockchain that stores and secures the transactions of cryptocurrencies such as Bitcoin.
When using a common currency traders trust a third party, the bank, that keeps a ledger of all transactions. When using a cryptocurrency, they put their trust instead into a blockchain: a public ledger of all transactions, split into blocks, packets of transactions, each containing around 2000 of them, immutably bound together. It is maintained (and replicated) by a network of thousands of computers to make it practically unforgeable: The whole network can read all the blocks and it will only accept the addition of valid blocks.
The Bitcoin network prevents the (malevolent) alteration of the (existing) blockchain by requiring a proof of work for appending a block to it: the computation of an input to a cryptographic hash function that yields an output with many leading zeros.
There are other approaches to make cryptocurrencies costly, for example:
the BurstCoin uses a “proof of space” instead of a
proof of work, that is, the reservation of a hard disk space, to earn
coins. Like the Bitcoin, it also has the drawback that all
transactions are public (with the knowledge of the person behind the
public key [the Bitcoin address] as the only
cover-up).
For increased privacy, the cryptocurrency
Monero uses group signatures (see Section 4.3) to confirm transactions between
traders, thus obscuring the cryptocash flow, andZcash which uses zk-SNARKs instead of
group signatures, a non-interactive zero knowledge proof.We will see
The blockchain, literally, is a chain of blocks. There is an initial block, the Genesis block and blocks that point to their predecessors. This arrow pointing to the predecessor is a hash, an identification of the entire contents of the previous block; it is an address that appears in the block header. The trunk of the block consists of an average of transactions between Bitcoin users.
Since the hash of the block depends on the entire contents of the block, the change of a single bit changes its hash, that is, invalidates the arrow pointing to its successor! Thus, for the blocks to continue to form a chain, this arrow must be changed. Thus, the hash of the successor block changes! Thus, for blocks to continue to form a chain, it is necessary to change the arrow of the successor of the successor, and so on; a chain reaction! That is, if we change one detail, for example, a transaction in the first block, all the arrows (= hashes) that follow must be recalculated!
Enters so-called “mining”, which makes this change very difficult, because only blocks whose hashes are small, that is, start with many zeros, are accepted by the network (that is, by its verifier nodes). Thus, it is not enough to change a transaction and calculate the new hashes of all successor blocks. This change has to be such that all blocks are accepted, that is, their hashes are small! It is highly difficult to find such a change: Currently, searching such a block takes a billion years on a regular computer; but only ten minutes on the mining network. While the bad guy started searching for admissible blocks, the network has already created several others, thereby invalidating his work!
All existing bitcoins were generated by mining, that is, they were given (by the coinbase transaction) as a reward to the one who created a block (with a small hash). All other transactions have an input and output: As input a sufficient amount is gathered together to pay what will be spent. Better almost the full amount be spent, because everything what is not spent will go to the miner who will eventually make this transaction happen (by including it in the block he mined). Therefore usually a transaction includes the sender as a recipient as well to receive the unspent money back; the change transaction (whereas usually only about bitcoin is paid to the miner as a transaction fee). The recipient is designated by his public key, and only at the time he will spend the received coins he will need to prove that he owns the corresponding private key, by signing the transaction.
Bitcoin uses encryption by finite elliptic curves to sign transactions: Diffie-Hellman uses finite rings of number such as (for example, for the clock, and a prime number such as with digits in Bitcoin). The concept used by Bitcoin resembles that of Diffie-Hellman, only instead of numbers , , , … it uses pairs of numbers that designate Cartesian coordinates of points on a (so-called elliptical) curve. The beauty of this curve is that one can add points on them: if these three points , and lie on the same line. Instead of multiplying the same number several times as in Diffie-Hellman, we add the same point several times. It is easy to add points, but it is very difficult to know how many times a point was added to itself to obtain the resulting point. Encryption corresponds to iterated addition, decryption to the knowledge of how many iterations.
Finally, the signature scheme is a variation of ElGamal’s signature: the signature shows that the owner of the private key was able to solve a difficult equation; so difficult that it is practically impossible to solve it without this private key that provides a shortcut.
How many transactions does a block of the Bitcoin blockchain contain on average?
How long does the addition of a block to the Bitcoin blockchain currently take on average on a regular computer?
The blockchain is a chain of blocks that are linked, that is, each block contains a hash of another block, which we think of as a pointer (or address) to the previous block.
Branches, orphaned blocks, occur; however, only the longest chain (more exactly, whose construction was computationally heaviest; see proof of work in Section 16.4) is considered valid. As it is very difficult to extend the chain by another block, branches rarely have more than one block.
The chain was lanced on January 3, 2009 at 18:15 UTC, probably by Satoshi Nakamoto, with the first block, the genesis block.
Each block consists
The hash of the block depends on all of its content. That is, (practically) any change causes its hash to change; for example:
For example:
In other words, a chain reaction occurs: The change of a single transaction in one block invalidates all the hashes of its later blocks.
Therefore, for the blocks to continue to form a chain, the pointers (that is, the hashes of the later blocks) of all the blocks that follow the changed block must be recomputed: Normally, these new blocks invalidate the blockchain because these new hashes no longer conform to the required pattern (= a sufficient number of leading s) to be accepted in the blockchain.
Each block groups transactions between users in a Merkle tree.
| Field | Description | Size |
|---|---|---|
| Magic | = 0xD9B4BEF9 | 4 bytes |
| Header | Contains 6 items | 80 bytes |
| Block | Size | 4 bytes |
| Number of transactions | 1 – 9 bytes | |
| Transactions |
Each block groups transactions (which have, on average, bytes). First its size (up to Megabyte) and number of transactions (on average ) are indicated.
The first transaction, the coinbase transaction, the
reward for the work done for its creation, is written by the creator of
the block and, therefore, commonly she and her collaborators are put as
recipients.
The other transactions are transmitted to the network by the senders, that is, payers, and all block creators, the miners, decide which transactions they include in the block they are creating. To encourage the inclusion of a transaction, the sender may pay a fee to the creator of the block; hence often the miner includes as many transactions as possible, about Megabyte.

The header of each block contains:
nonce, a field without (semantic) content, which
serves to change the hash of the block without changing its (semantic)
content.The cryptographic hash function used by Bitcoin is
SHA-256. In more detail:
| Field | Updated when… | Size |
|---|---|---|
| Version | the software is updated | 4 bytes |
| Hash of the previous block | a new block is created | 32 bytes |
| Hash of the tree root | a transaction was accepted | 32 bytes |
| Date of creation | a few seconds passed | 4 bytes |
| Difficulty | every -th block | 4 bytes |
| Nonce | another hash is proven | 4 bytes |
The “body” of the block, its content (in contrast to the header metadata), is formed by the transactions. These are grouped in a “Merkle” tree, a (usually binary) tree of hashes where the hash of a node is calculated by those of its successors; the data, here the transactions, constitute its leaves.
The nonce is used to search for a block with a
sufficiently small hash without changing its (semantic) content. For
quite some time the
bytes of the nonce are insufficient to find a sufficiently
small hash. That is, after
increments, no found hash is small enough. In this case,
ExtraNonce, the coinbase transaction message
(which has
bytes) is iterated. However, then the hash of the Merkle tree root needs
to be recomputed.
The first transaction, the coinbase transaction, the
reward for the work done for its creation, is created by the creator of
the block and, therefore, commonly he and his collaborators are the
recipients. Each transaction has
In all (except the initial transaction) the input collects outputs from transactions (by referring to their hashes) whose sum is greater than (or equal to) the sum of the outputs. In the initial transaction of the block, the input is arbitrary, and the amount is the reward given to the miner, initially bitcoins, in 2021.
The first block of the chain, mined by Satoshi Nakamoto, the anonymous creator of Bitcoin, contains the title of page one of the Financial Times:
The Times 03/Jan/2009
Chancellor on brink of second bailout for banksHowever, as mentioned above, the content nowadays is often not human readable; instead, it is a value for technical purposes, for example, to alter the block such that its hash is small enough.
To append a block to the blockchain, a proof of work must be
given, the calculation of (a head of) a block such that its
hash is small, that is, that its binary expansion starts with a large
number of zero digits (in January 2021, with
zeros in the hexadecimal expansion or
zeros in the binary expansion). Perhaps the most used software for this
purpose is currently CGMiner; there are
versions for all operating systems, some adapted for graphics processors
(GPUs) and others for processors specifically programmed
for mining (ASICs).
The hash of a mined block on January 13, 2021:
000000000000000000010f32aa4a0a862d4761ae7a997fbf8590ce2191dfc064While the high computational cost is useless to build a blockchain, it is essential for its integrity because it makes it practically impossible to (malevolently) alter previous blocks. That is, it ensures the irreversibility of the blockchain: Once a transaction is in a block which has been extended by, say, at least five other blocks, it is practically impossible to replace the blockchain blocks because every such effort is outpaced: while these blocks are hard searched for, the blockchain has already been extended by other blocks.
Since each block contains in particular as an entry the hash of the previous block, and the hash of the entire block depends in particular on this entry, changing a block requires changing every subsequent block; since each block needs a hash with many initial zeros to be accepted into the blockchain, it is hard to find these subsequent blocks. A lot of work against time:
To change a block in the chain, the single miner needs to
This irreversibility lets one dispense with a third party for the traders, that is, a fiducial authority. Instead, it is the nodes of the network agree on the validity of the transaction.
However, if a miner has more computing power than all other miners, then he can apply the % attack:
A proof of work shows information that is computationally costly to obtain. Often, the work consists of repeating an operation till an unlikely event occurs, that is, brute force.
Bitcoin uses the proof of work introduced by
Hashcash to prevent spam by a proof of work required for
the sending of each email to each recipient; so that the proof of work
makes mass sending costly.
In Bitcoin, the proof of work is required to extend the chain by a new block.
The work consists in searching for a block whose hash with
bytes by the SHA-256 algorithm is less than a certain
target number:
Other common Hash algorithms (instead of SHA-256) for
proof work are, for example,
We iteratively append to the string “Hello, world!” a
nonce, a number used once, such
that (the hexadecimal expansion [with the
digits
–
and
–
])
of its SHA-256 hash starts with 0000. There
are
combinations of four hexadecimal digits; so if the values of the hash
function are uniformly distributed, then we expect about
attempts to find it. In fact, after
attempts, which take a millisecond on a modern computer, we obtain:
"Hello, world!0" => 1312AF178C253F84028D480A6ADC1E25...
"Hello, world!1" => E9AFC424B79E4F6AB42D99C81156D3A1...
"Hello, world!2" => AE37343A357A8297591625E7134CBEA2...
...
"Hello, world!4248" => 6E110D98B388E77E9C6F042AC6B49...
"Hello, world!4249" => C004190B822F1669CAC8DC37E761C...
"Hello, world!4250" => 0000C3AF42FC31103F1FDC0151FA7...However, in Bitcoin, the hashed object, the block header, is more complex, in particular because it contains the root of the (Merkle) tree of transactions.
The ‘difficulty’ field in the block header compares
with
Initially, for the “Genesis” block to be accepted in the chain, the
binary expansion of the hash of its header needed to start with
zeros (= the size, in bits, of the nonce in the block
header); that is, it took
)
computations of hashes to find a block with such a hash (taking a couple
of minutes on a notebook).
Since then, the number of zeros has been readjusted after every -th block to ensure that the computation of a new attachable block over the network takes, on average, minutes. (That is, computing new attachable blocks takes on average weeks.)
Each readjustment (after blocks) calculates the new difficulty as a ratio between
that is, To avoid too steep a jump, the new difficulty is . That is, even if (that is, the network took less than three and a half days to append blocks), then the new difficulty is .
Computing a block header whose hash is smaller than the current target, that is, whose binary expansion begins with enough zeros, is called mining.
The difficulty is at each moment (with a delay of at most two weeks) proportional to the joined computational force of the miners: The more miners, the more difficult, the fewer miners, the easier. Currently, in 2022, the binary expansion of the hash has to start with around zeros to be accepted by the network.
Since the hash used in bitcoin is cryptographic (currently
SHA-256), that is, its output doesn’t allow deducing the
input, the only practical way to find a header such that its hash is
small enough is by brute force, that is, trying out all
possible combinations one after another. Since a hash function is almost
uniformly random, that is, the probabilities of all outputs are almost
equal, it takes on average about
attempts until a header whose hash has a binary expansion starting with
zeros is found.
Intel Core i7 2600, computes around
=
million hashes per second. That is, it takes on average around
seconds
(
years, that is, a billion years).This gives an idea of the current combined computational power of the
miners, since they calculate this hash on average in ten minutes. Since
the hash function used by Bitcoin is SHA-256,
as discussed in Section 3.7, it is quickly
computed by a CPU, a microprocessor for general use on a
personal computer, and in particular,
GPU, by a graphics
processor; about
times faster than a CPU, andASIC, a
microprocessor suitable for a specific application such as the
computation of SHA-256; it is about
times faster than a CPU.In fact, the energy expenditure for mining is equivalent to that of the whole of Austria at any given time. For this reason, alternative concepts to the proof of work have emerged, for example, the proof of stake where the owner of the next block is determined by how much she owns instead of how much she can compute. However, so far these alternative concepts have not worked so well in practice.
Once such a block and its hash are found, given both, the verification that the hash is small enough is quickly done: simply compute the hash of the block and compare it to the given hash.
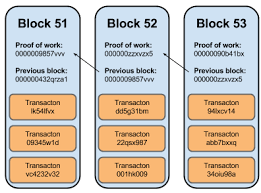
The interval to create a new block is, on average, minutes. While it will not always take almost exactly ten minutes or less, as a Poisson process the probability of a block been found in this minute range is about (more exactly, the probability is ).
To change the block header, let us recall that the changeable header data consists of (cf. Section 16.3)
nonce, a field without (semantic) content that
serves to change the hash of the block without changing its (semantic)
content.In particular, the main content of the block, the transactions, enters into its hash only indirectly through the hash of the root of the Merkle tree.
Currently, since the number of initial zeros in the binary expansion
of an admissible hash
and the field nonce only has
bytes (=
bits), rarely (that is, with a probability of only about
)
there is a value of the nonce such that the block hash is small enough.
Therefore the miners change, in addition to the nonce,
timestamp, the creation date in seconds counted
from 1970-01-01 at 00:00 UTC, coinbase, the message (having
bytes) that accompanies the first transaction of the block and transfers
a reward to the miner for having found the block with a hash accepted by
the blockchain network. While coinbase provides ample space
to change the hash, it is a more expensive option than
timestamp or hash because, being part of the
transactions, its change implies the recomputation of the hashes of the
Merkle tree that stores the transactions. (Recall though that it is only
the root hash of the tree that enters the block header.)When a new block is discovered, the miner transmits it to the network, and the nodes check, among others:
After the blockchain has been extended by at least other blocks following this block (so that the network ensured that this blocks will persist in the blockchain, the longest chain), its finder:
As the reward gradually fades out (until it runs out after blocks), these transaction fees will play a more and more important role in encouraging the miners to hold on mining.
To distribute the unpredictable reward from mining more evenly, many
miners join their computational forces in groups, clusters,
to share the rewarded bitcoins.
All bitcoins are generated by mining: The miner, the creator of the
block, can freely choose the recipients of the first transaction of the
created block, the coinbase transaction.
Once generated, a bitcoin changes place by a chain of
digital signatures: A bitcoin is transferred by its
owner
The sum shown in the Bitcoin Core graphical user
interface (initially developed by Satoshi Nakamoto under the name
Bitcoin-Qt and used by
% of the traders) is the sum of all transactions that the owner
received: For Alice to pay a certain amount, for example,
bitcoins, to Bob, the program
bitcoin to Alice.That is, Alice received another transaction (although of a smaller value than the two initials).
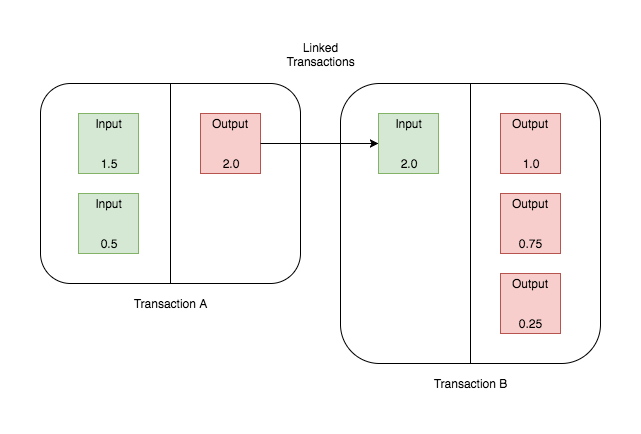
The identity of each trader corresponds to his asymmetric key
(ECDSA), a pair of
To get his address, several hash functions are applied to
the public key. Then the final sequence of
letters is coded by the Base58 whose
numbers are
0O and the letters
Il for the risk of mixing the letters of each pair up.To calculate the hash of the public key:
ECDSA,RIPEMD-160 (to the last result), and0x0000 for P2PKH,
0x0005 for P2SH).To add a checksum:
SHA-256,SHA-256,To abbreviate the result (in a human-readable way):
Base58.To see it in in action, visit https://gobittest.appspot.com/Address.

To get the scriptPubkey format used in transactions:
Base58 to hexadecimal base,and finally add a certain instruction code.
The use of a hash instead of the public key as the address, besides shortening it,
ECDSA) will be
compromised one day, andA transaction is a bitcoin transfer, first transmitted on the network, then collected in a block by a miner and published. All transactions are public, while (the hashes of) the public keys are anonymous, that is, they do not reveal a priori the owners’ names.
There are two types of transactions:
In more detail:
a generation transaction is determined by the miner:
coinbase field (instead of scriptSig)
whose content is arbitrary. (It is often (ab)used as
ExtraNonce, that is, additional Nonce
for mining, since the size of Nonce,
bytes, is currently insufficient to find a block whose hash is small
enough. However, unlike the Nonce field,
ExtraNonce only indirectly enters the transaction through
the hash of the Merkle tree root. Therefore, modifying
ExtraNonce requires recomputing the hashes of the coinbase
branch into the Merkle tree of transactions).output distributes the reward (of
bitcoins, plus the earned transaction fees, in 2021) to the recipients
favored by the miner.a payment transaction has
an ‘input’, that lists transactions in which the sender received bitcoins, and
an ‘output’ that transfers to the recipients an amount equal to the sum of the sender’s received bitcoins.
Often, the transaction includes an exchange, that is, the sender appears as one of the recipients: If the sum is smaller, the difference is paid to the miner of the block that included the transaction as an incentive to swiftly consider it.
Once a block is included in the chain, and this block is extended by a sufficient number () of other blocks, the transaction can be considered irreversible; it is confirmed.
In the bitcoin network, there are
A miner is incentivized
However, the miner has no incentive to forward a block mined by someone else to the node network. Instead, he rather hides its existence until he has mined an own block that extends it. This instantaneous transmission is up to the nodes.
A user is incentivized to maintain a node to ensure the integrity of the blockchain at all times. However, maintaining an entire node is above all an altruistic need that is essential to the functioning of blockchain: The chain is only safe using a partial node (which only knows part of the chain) while there are sufficiently many full nodes in the network that guarantee the validity of the blockchain.
We summarize how a transaction is processed, from its emission to its accomplishment:
Send a transaction through your portfolio application.
The transaction is diffused by the nodes and becomes part of the pool of unconfirmed transactions.
Miners
Each miner tries to modify the block so that its hash becomes small enough (currently starting with null bytes). The probability of finding such a block, that is, the difficulty of the problem, is the same for all blocks and miners. This difficulty is adjusted every -th block (that is, after about two weeks) so that the miners’ total computational power to find such a block takes on average ten minutes.
When a new block is appended to the chain, all the miners have to start again with another block since
Every miner who found a valid block transmits it to the network nodes.
The node validates the block, that is, checks whether
If the node confirms the validity of the block, then it appends it to the chain. A confirmation of a transaction is each extension of the chain by a block after the block containing the transaction. The extension of the chain by the block containing the transaction counts as the first confirmation, the block after this one as the second confirmation, and so on. The probability that the last six confirmations (after an average of one hour) are undone is practically zero. Therefore, a transaction is usually seen as accomplished after its sixth confirmation.
For the node to quickly check the validity of a transaction entry,
that is, if the cashed in transactions have not yet been spent, he
steadily updates the Unspent Transaction Ouput
(UTXO) database of all transactions that have not yet been
spent. Currently, the UTXO has about
GB and is stored in memory to ensure fast queries.
Let us recall that each transaction is unique, and can be spent only once and entirely. When a transaction is transmitted,
UTXO, andUTXO.To prevent double spending, the node checks whether an outgoing
transaction is in the UTXO: if so, it allows the
transaction, otherwise it prevents it.
Let us recall that a confirmation of a transaction is each extension of the chain by a block after the block containing the transaction. The extension of the chain by the block containing the transaction counts as the first confirmation, the block after this one as the second confirmation, and so on. Because it is practically impossible that the last six confirmations (after an average of one hour) are undone, a transaction is usually seen as accomplished after its sixth confirmation.
For example, the default graphical interface for bitcoin,
Bitcoin Core, shows a transaction as confirmed when the
confirmation count reached
.
However, this number of confirmations
is arbitrary.
In contrast, bitcoins mined can only be spent
after the generated block has achieved a confirmation count of
.
The blockchain replaces a third trusted party, the bank, that mediates financial transactions, by a database of entries that successively point to each other. This pointer is a hash of the whole previous entry, ensuring the database’s integrity: thus, a change of the previous entry entails a change of the hash, thus invalidates the pointer, thus the whole chain. Because the hashes must have many leading zeros, finding valid entries, mining, demands much computational power and practically makes malevolent alterations impossible.
How long does the addition of a new block to the Bitcoin blockchain take on average?
Availability of URLs: Even after a certain URL
URLhas expired its content will still be available at thearchive.orgunder the URLhttps://web.archive.org/web/URL. For example, the finite field function plotter http://graui.de/code/ffplot/ is available under https://web.archive.org/web/http://graui.de/code/ffplot/. In this case, the page was archived on May 5, 2018; its status on this date is available at https://web.archive.org/web/20180505102200/http://graui.de/code/ffplot/.