UFAL, Maceió — Inverno 2019
Inverno 2019
A criptografia é a arte da transformação de um texto (ou qualquer outro arquivo) compreensível em um texto incompreensível tal que só uma informação adicional secreta, a chave, permita desfazê-la; útil desde a antiguidade, por exemplo, para ocultar do inimigo a comunicação militar.
O livro primeiro estabelece a diferença entre
e
Um sobrevoo da História da criptografia apresenta os algoritmos simétricos da antiguidade que servirão como pedras angulares dos algoritmos criptográficos simétricos modernos, as redes de permutação e substituição, como o atual padrão AES.
Este é percorrido passo a passo para compreender a sua invulnerabilidade contra os ataques mais sofisticados para decifrar o texto cifrado por ele sem conhecimento da chave.
Entra nos anos 70 a criptografia assimétrica, indispensável na idade da internet e ubíqua no nosso dia-a-dia, por exemplo, para cifrar os mensageiros do celular, sites seguros no navegador e transações financeiras à distância. Sofre, porém, do ataque pelo homem no meio que assume as identidades dos correspondentes, o que leva à infraestrutura de teias de confiança, autoridades e certificados, visualizados por cadeados na barra de endereço no navegador.
Por trás de toda a criptografia assimétrica figura a Aritmética Modular que permite criar uma aplicação invertível (chamada de arapuca) cujo inverso é praticamente incomputável. Exemplos são a potenciação respectivamente a exponenciação modular que são usadas pelos dois algoritmos fundamentais da criptografia assimétrica:
RSAque são ambos estudados passo a passo e cujas bases teóricas são motivadas e explicadas.
Ultimamente a criptografia por curvas elípticas finitas, um grupo finito de pontos num reticulado no plano, tornou-se o novo padrão da criptografia assimétrica. A sua aplicação arapuca é análoga à do Diffie-Hellman, assim como os passos da cifração e assinatura, mas pela sua maior complexidade mais segura.
Elas são usadas, por exemplo, para assinar as transações na criptomoeda Bitcoin cujo conceito e funcionamento é desenvolvido na parte final do livro: Ao contrário de uma moeda comum na qual os negociantes confiam em um banco, uma criptomoeda mantém um livro-razão público de todas as transações. Para garantir a sua imutabilidade, ele precisa de funções de embaralhamento (ou hashes) que têm vários usos na computação, os quais são todos apresentados e comparados no penúltimo capítulo. O último capítulo examina a anatomia do livro-razão, a Blockchain ou, literalmente, cadeia de blocos: os seus blocos e os laços entre eles (os hashes). Em seguida responde às questões como ela
Historicamente, a chave para codificar e descodificar é a mesma: a cifração simétrica. Nos anos 70, surgiu a cifração assimétrica, na qual as chaves para cifrar (a chave pública) e decifrar (a chave secreta) são diferentes. Matematicamente, ela baseia-se em uma função alçapão, uma função invertível que é facilmente computável, mas cujo inverso é computacionalmente inviável.
Hoje em dia os algoritmos de cifração assimétrica têm altíssimo valor comercial: Toda hora, seguram e certificam milhões de transações financeiras na internet; quanto mais seguros os algoritmos, tanto mais as transações.
Distinguimos entre
A criptografia (simétrica) histórica trata textos e dispõe de duas operações:
Por exemplo, a Enigma usada pela Alemanha na Segunda Guerra Mundial usava apenas o primeiro recurso, a substituição das letras do texto claro pelas letras permutadas do alfabeto.
A criptografia simétrica moderna trata dados, isto é, bites, baites ou números em geral em blocos (Cifras de Feistel como o AES) e itera estas duas operações,
além de aplicar uma operação matemática como a multiplicação de matrizes, para obter ótima difusão (isto é, filosoficamente, cada letra do texto cifrado depende de todas as letras da chave e do texto claro).
A primeira parte trata a questão ubíqua da confiança. Como a criptografia assimétrica permite obter a chave por uma fonte anônima, como garantir que seja confiável? Quer dizer, como evitar o perigo do ataque do man-in-the-middle em que o atacante se interpõe entre os correspondentes, assumindo a identidade de cada um, assim observando e interceptando suas mensagens?
Na segunda parte, tratamos das ideias matemáticas por trás da implantação dos algoritmos de criptografia assimétrica:
Introduzimos as ferramentas básicas para tratar a criptográfica assimétrica, que é matematicamente mais rica: Por trás de todos os algoritmos criptográficos é o problema da insolubilidade computacional do logaritmo discreto, o que muda a figura é o grupo sobre o qual ele opera. Os exemplos principais são
Estudamos primeiro o caso clássico, o grupo multiplicativo de um corpo finito: Revisaremos as bases matemáticas, números primos, aritmética modular e corpos finitos, para então tratar os algoritmos mais antigos (dos anos 80) baseados nelas: os algoritmos
Concluímos com o caso mais recente, o grupo aditivo de uma curva elíptica: As suas bases matemáticas são mais envolvidas, com efeito, baseiam-se na teoria dos corpos finitos.
Os meios criptográficos para implementar uma criptomoeda como o Bitcoin são
O primeiro capítulo não-numerado, Introdução,
O segundo capítulo não-numerado, Notações, é um glossário das noções e notações usadas.
Este capítulo estabelece a diferença entre a criptografia simétrica, usada desde a antiguidade, e a criptografia assimétrica, inventada nos anos 70. Em particular, destaca a importância da assinatura digital, possibilitada pela última. Mostra como quaisquer dados, sejam textos ou imagens, se codificam em arquivos digitais, isto é,
Este capítulo dá os exemplos históricos da criptografia (simétrica) dos romanos e espartanos que servirão como protótipos para algoritmos modernos.
Discute a segurança destes algoritmos e mostra como podem ser quebrados por regularidades estatísticas apesar de um grande número de chaves.
Desmantela a Enigma, máquina criptográfica usada pelos eixos de potências, em particular, pelos alemães durante a Segunda Guerra Mundial. Delineia como ela foi quebrada pelos aliados apesar de ser teoricamente segura.
Este capítulo apresenta AES, o atual algoritmo padrão da criptografia simétrica, e mostra como os algoritmos antigos servem como suas pedras angulares. Motiva porque ele é considerado imune contra os ataques mais valentes conhecidos. Explica em particular o ataque da Criptoanálise Diferencial e mostra a imunidade do AES contra ela.
Este capítulo sobre a criptografia assimétrica discute
Salienta a indispensabilidade da assinatura digital para assegurar toda negociação (financeira) online.
Orienta sobre as melhores práticas para o gerenciamento das chaves públicas e privadas; em particular, como guardar as chaves privadas da forma mais segura possível.
Introduz ao uso do o atual padrão GPG para criptografia assimétrica, e apresenta uns aplicativos, tais como mensageiros, que a usam (entre eles WhatsApp).
Este capítulo estimula o leitor a estudar a base de toda a teoria por trás da criptografia assimétrica, a Aritmética Modular, pela sua utilidade na criptografia assimétrica.
Este capítulo dá os passos do protocolo criptográfico assimétrico mais antigo, dos anos 70, a troca de chaves por Diffie-Hellman, e explica porque é considerado seguro até hoje.
Este capítulo prepara a estrada para o algoritmo assimétrico mais usado até hoje, o RSA, pela apresentação do Algoritmo de Euclides, uma iterada divisão com resto, em que ele se baseia.
Este capítulo dá
RSA, e explica porque é considerado seguro até hoje, eElGamal que se baseia no Diffie-Hellman e serve como protótipo para muitos protocolos de assinatura como o DSA e EC-DSA.Este capítulo introduz a criptografia pelas curvas elípticas finitas, o novo padrão da criptografia assimétrica e atualmente considerado mais eficiente. Compara as suas vantagens e inconveniências com o Diffie-Hellman ou RSA.
Este capítulo prepara as ferramentas principais para as criptomoedas baseadas na Prova de Trabalho (tal como o Bitcoin) pela introdução das funções de embaralhamento ou funções hash. Os seus valores servem como (carteiras de) identidade de arquivos. Existem vários usos delas na computação; logo, existem diferentes tipos delas com diferentes finalidades os quais apresenta todas.
Este capítulo explica
Bitcoin:
Bitcoins são (seguramente) guardados e transferidos?Excelentes livros de referências para acompanhar o curso são
Lembremo-nos de que, mesmo se o link URL expirou, o conteúdo é ainda disponível pelo archive.org no endereço https://web.archive.org/web/URL/ . Por exemplo, o plotter de funções sobre um corpo finito http://graui.de/code/ffplot/ ficará disponível sob https://web.archive.org/web/http://graui.de/code/ffplot/ . Neste caso, a página foi arquivada no dia 5 de maio 2018; o seu estado nesta data continua a estar disponível em https://web.archive.org/web/20180505102200/http://graui.de/code/ffplot/ .
Esta secção explica a linguagem matemática básica, conjuntos e funções. Como as notações usada na matemática acadêmica diferem em uns pontos das do ensino escolar, repitamos as mais comuns:
A noção fundamental da matemática é a de um conjunto; segundo os dicionários Aurélio, Houaiss ou Michaelis:
Esta coleção de seres matemáticos é denotada por . Se um ser matemático pertence ao conjunto , dizemos que é em e escrevemos ou .
Por exemplo, o conjunto
Podemos comparar dois conjuntos e :
Podemos formar um novo conjunto a partir de dois conjuntos e :
Por exemplo, os números irracionais são todos os números reais que não são racionais, isto é, que pertencem ao .
Denote o seu produto cujos elementos são para em e em , isto é, Se , escrevemos em vez de , e em vez de , e assim por diante. Por exemplo, é o plano (euclidiano), e é o espaço.
Uma função descreve a dependência entre duas quantidades. No ensino escolar, é usualmente denotada por uma equação onde na expressão figuram
Por exemplo:
Porém, existem outras dependências, por exemplo:
Definição. Uma função é uma regra que associa a cada elemento de um conjunto exatamente um elemento de um conjunto .
Esta associação é simbolicamente expressa por . Refiramo-nos
A de é o conjunto de todos os valores de , Por exemplo, e para a função constante . O contra-domínio contém a imagem, mas não necessariamente coincide com ela,
Usualmente, vemos funções com e , isto é, funções reais; chamamo-nas muitas vezes simplesmente de funções. Usualmente as letras denotem números reais; as letras denotem números naturais (usados para enumerações). Nos nossos exemplos:
Funções reais aparecem em diversas formas: além de
obtemos pela substituição da variável por um número real como , , , , …
uma tabela de valores e dado pela avaliação do lado direito da igualdade , e
um gráfico
Em mais detalhes:
Na forma de uma equação como nos exemplos acima: , por exemplo, Para facilitar, fazemos o convênio seguinte: Se escrevemos apenas a regra de associação, por exemplo, ou , então o domínio é o subconjunto máximo de para que esta regra seja definida (quer dizer, faça sentido). Por exemplo, nestes exemplos, e .
Na forma de uma tabela de valores, por exemplo: Um experimento mede a tensão de um resistor em dependência da corrente . A tabela tem as entradas e . Aqui (e ). (Gostaríamos de extrapolar esta função, isto é, estender o seu domínio a ; a este fim, parece provável que com .)
A equação funcional associa a cada valor um único valor , em símbolos, . Um tal par de valores pode ser interpretado como ponto no plano cartesiano. Para cada par de valores obtemos exatamente um ponto. Dado um ponto , os números reais e são chamados das coordenadas (cartesianas). O conjunto de todos os pontos forma a curva da função (ou gráfico), que ilustra o percurso da função . (Por exemplo, a parábola ou uma função afim .)
Para desenhar a curva:
Enche uma tabela de valores para uns argumentos , , …
Desenha os pontos dados nela, e
Conecta-os para obter o percurso da curva da função.

De vez em quando, para destacar que um objeto, por exemplo, uma função , depende de outro objeto, por exemplo, de um conjunto ou uma ênupla , escrevemos ou respetivamente ou em vez de .
No ensino acadêmico, uma função ou aplicação é denotada por para os dois conjuntos,
dizemos que manda ou envia cada argumento em a um único valor em .
Lê-se que é uma função de a , ou tem argumentos em e valores em . No contexto informático, pensamos de como um algoritmo, e referimo-nos a e como entrada e saída.
Uma função manda ou envia cada argumento em a um único valor em (ou associa a cada um único ). Escrevemos e denotemos este valor por . Frequentemente, ou e ou . Por exemplo, a função dada por manda em a em .
Função e aplicação são sinónimos. Contudo, a conotação é outra: Se os objetas do domínio são, por exeplo, números inteiros, conjuntos, então aplicação é mais comum, enquanto função é principalmente usada quando o domínio consiste de (ênuplas de) números reais.
A partir de duas funções e (sobre quaisquer domínios e imagens) pode ser obtida outra por concatenação; a função composta ou a composição , dado que a imagem de é contida no domínio de , isto é, . É definida por simbolicamente, para obter , substituímos em por .
Se temos duas funções, isto é, tais que os valores de são argumentos de , a sua composição é definida por isto é, a saída de é a entrada de , e denotada por
Por definição, uma função associa a cada argumento exatamente um valor . Frequentemente surge o problema inverso: Dado um valor , determina o seu argumento sob , isto é, tal que . Se uma função é injetora, isto é, implica , isto é, a argumentos diferentes são associados valores diferentes, então a cada valor é associado um único argumento . A função obtida pela associação inequívoca inversa , ou é a ou o de e denotada por . Ora, é a variável e a variável . Em fórmulas, a função inversa é obtida pela permutação das duas variáveis e na equação .
Matematicamente, a função tem o inverso , se e . Por exemplo, sobre vale para , e para e .
Para desenhar a função inversa, poderíamos permutar as designações dos dois eixos. Porém, isto comumente não se faz. Porém, se o domínio e a imagem coincidem, o gráfico da função inversa é o espelhamento do gráfico da função invertida na diagonal dos pontos cuja coordenada é igual à coordenada .
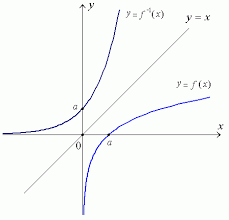
Exemplos. Olhemos uns exemplos de funções invertíveis. Observamos em particular que a invertibilidade depende do domínio: Quanto menor o domínio, tanto mais provável que a função seja invertível.
Resumimos:
Um número real no dia-a-dia é escrito em notação decimal com , , , , , em . Isto é, é como soma em potências de e com algarismos , …, . Por exemplo, Em vez da base decimal , existem outras. As mais comuns na informática são
Isto é,
Por exemplo, e
A criptografia serve a proteger dados, e consegue isto por um embaralhamento (cifração) que praticamente pode unicamente ser invertido (decifração) com uma informação adicional secreta, a chave.
Outrora, a criptografia estudou a transformação de um
tal que só uma informação adicional secreta, a chave, permita desfazê-la.
Hoje em dia, a criptografia estuda a transformação de
tal que só uma informação adicional secreta, a chave, permita desfazê-la.
| dados | = | arquivo digital (de texto, imagem, som, vídeo, …) |
| = | sequência de bites (= 0, 1) | |
| = | sequência de baites (= 00, 01, …, FE, FF) | |
| = | número (= 0, 1, 2, 3 …) |
Isto é, toda sequência de bites é uma número pela sua expansão binária e vice-versa.
A – F correspondem a um grupo de quatro bites) é preferida na criptografia simétrica cujos algoritmos transformam-nas, por exemplo, por permutação e substituição dos seus dígitos.Dados referem-se classicamente, antes da época digital, a textos, hoje em dia a qualquer arquivo digital, sejam textos, imagens, sons, e assim por diante. Nos nossos exemplos, sempre suponhamos que os dados sejam um texto. Quando assumirmos o ponto de vista matemática, os dados referem-se a um número natural, isto é, um elemento em , , , , …
Mostramos pelos exemplos de textos e imagens como esta codificação, dos dados em (sequências de) números se faz: Recordemo-nos de que
Um texto é uma sequência de símbolos. Há várias codificações que associam a cada símbolo um número; as duas mais conhecidas são
ASCII, que cobre todos os caracteres ingleses (e os símbolos de pontuação) e que envia um símbolo a um baite,UTF-8, que inclui a ASCII e cobre todos os caracteres de todos os idiomas (por exemplo, do chinês, coreano, … e além disso, por exemplo, todos os símbolos matemáticos) e que envia um símbolo a , , ou até baites.Por exemplo, Com efeito, o ASCII somente predetermina a codificação dos números , isto é, todas as sequências de bites que começam com 0. Depois do ASCII,para internacionalizá-la, surgiram inúmeras codificações (por exemplo,
ISO-8859-1 ou ISO-Latin-1 para os alfabetos latins na Europa ocidental eISO-8859-5 para os alfabetos cirílicos usados na Europa oriental (por exemplo, na Bulgária ou Sérbia) e na Rússia.Todas elas ocuparam o espaço dos números para acrescentar os símbolos do próprio alfabeto, isto é, todas as sequências de bites que começam com 1.
A codificação UTF-8 teve uma abordagem mais engenhosa: O número dos dígitos binários consecutivos iniciais iguais a nos primeiros bites, acrescentado por , iguale o número de baites, de a , do símbolo codificado. Isto é, ela envia um símbolo a , , ou até baites, onde
Por exemplo, o símbolo ç, a letra c com uma cedilha, tem baites e Vemos que, com efeito, o número dos primeiros coeficientes consecutivos iguais a é (como já o segundo coeficiente é igual a ), o que, acrescentado por , resulta em , o número de baites de ç.
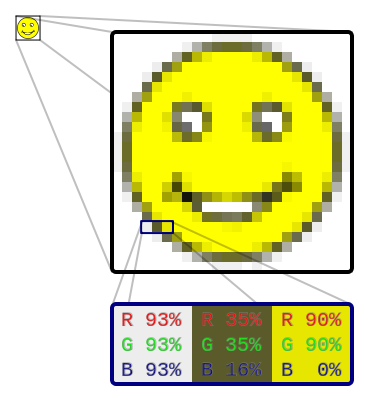
Para imagens, o formato mais simples é o de um bitmap, um mapa de bites. Uma imagem
é um conjunto de pixeis (por exemplo, ),
cada pixel é uma cor, e
cada cor é os seus graus de intensidade da luz das três cores primárias
O homem não consegue distinguir mais de 256 graus de cada cor primária,
basta codificar cada pixel por três baites.
Recordemo-nos de que a chave é a informação adicional secreta que pode ter várias formas a qual é sobretudo uma questão da conveniência. As mais usais são a
Por exemplo, no algoritmo antigo da Cítala ou bastão de Licurgo, a chave consiste da circunferência (em letras) do bastão usado, um número. Hoje em dia, um código PIN (= Número de Identificação Pessoal) ou senha são omnipresentes no nosso dia-a-dia; para facilitar a decoração, para datas muito sensíveis, é encorajada a decoração de completas frases (= múltiplas palavras) secretas.
A criptografia assimétrica depende de chaves maiores e por isso as armazena em arquivos (de textos com letras, chamados de ASCII-armor) de alguns quilobaites.
Historicamente, a chave para inverter a transformação (de dados inteligíveis em dados ininteligíveis) era tanto necessária para decifrar quanto para cifrar, a criptografia simétrica. Já foi usada pelo egípcios quase 2000 anos antes de Cristo.
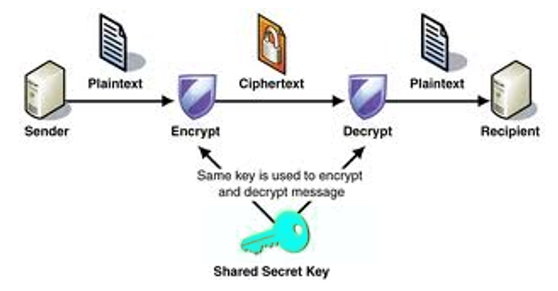
Nos anos 70, surgiu a criptografia assimétrica, na qual as chaves para cifrar (a chave pública) e decifrar (a chave privada) são diferentes.
Com efeito, só a chave para decifrar é privada, guardada secreta, enquanto a para cifrar é pública, conhecida a todo mundo. (Porém, é possível, e muitíssimo útil, que as chaves trocam os seus papéis, a chave privada cifra e a pública decifra, a assinatura digital, explicada mais em baixo.)
Em comparação a criptografia simétrica, a criptografia assimétrica evita o risco de comprometimento da chave para decifrar envolvido
Em particular o primeiro ponto, que permite comunicar seguramente com qualquer pessoa através de um canal inseguro, é uma grande vantagem em comparação à criptografia simétrica! Tão grande que, enquanto antes da era da internet a criptografia assimétrica era impensável, depois a internet ficou impensável sem a criptografia assimétrica.
A um nível de segurança comparável, os algoritmos da criptografia simétrica são mais econômicos que os da criptografia assimétrica.
Aqui mais econômicos quer dizer que os algoritmos simétricos
RSA usa chaves de pelo menos bites, enquanto o algoritmo simétrico AES usa chaves de bites. (Esta diferença será explicada em Seção 9.5.)Esta diferença se reflete pelo gerenciamento entre uma chave assimétrica ou simétrica:
passphrase) que o usuário decora.MD5 ou SHA-256 a uma sequência de byes de um comprimento determinado, por exemplo, de baites. Padroniza o comprimento da chave e cifra para evitar uma leitura por outra pessoa.)Exemplo de uma chave pública codificada em ASCII:
-----BEGIN PGP PUBLIC KEY BLOCK-----
Version: SKS 1.1.6
Comment: Hostname: pgp.mit.edu
mQENBFcFAs8BCACrW3TP/ZiMRQJqWP0SEzXqm2cBZ+fyBUrvcu1fGU890pd43J diW
IreHx/sbJdW1wjABeW8xS1bM67nLW9VVHUPLi9QP3VGfmqmXqbWIB7OxizZ PTDCWm
oymm/+TlTTAZWU6Wwvmjk88QlmU941tUvBsQ1cw1cAxw+2jLCgkz8XvW npMPKKj1f
sNZ/FcPVMC6dkwHAFc7Rm4DNibJzLvD8woL0vAdUR4HhOQli9+Fpv UO0KVVhOwF0f
14EURddA4qZVyPM8e3FvxiWF0JWJuxCuiBHh5ghT/Q+OQMMOJW VTwME5nQ87vohfX
gjRbYjW8gyLRqIjt2Gc7dNgIoKE5r/PABEBAAG0I0Vubm8g TmFnZWwgPGVubm8ubm
FnZWxAdC1vbmxpbmUuZGU+iQE5BBMBAgAjBQJXBQLPAh sDBwsJCAcDAgEGFQgCCQo
LBBYCAwECHgECF4AACgkQVJDsz4ujnoR03gf9HIIc pOSI1yokf6JZjH/Oon+FDoJd
7i7B1wfMyOKmSDsTbrJqimi7s8R9hsSljYuf/s TzMbGGCoHkOfnZyGuv3HovTO90x
g5JSsCTU/DhojHqANODJ23lTZFgW0vOmxkL KpRKOPiZ+xX3z9PjDNULFCBLV4s2+m
UABKbkKJLecytE8g4WWDkV7ePHrkTZyS sAoaNvLW6f0BxGmO0L4Igf35UG2ZbzMah
m8eFu6ADr3gQKO1DaiOhQsF5oInGq ymyaZyNCMR0CohWZuGT1DLVFUOzGos1p42Tl
BqylUJGw8ll9xeQJevAMf2xdrl DyRNxyy6ojOjXMzmf32CPQpI7JN7kBDQRXBQLPA
QgAwL9sFKBf2h8KLjHkfSXD EMMVgKdifO9J6F0ubS8l4vXj+DlnJusjxa7oLMIrxp
BT35y06pohtqwKMsxGEZ Uvx9MKk1NdU5OksPyvoSSVcIm4APzC/1pSFaHUjlWp3HI
4PC5yFBo3IMqIajtu PyYOB3A8O5iIIm8ip1BvEVHTruAOz/1wIFr+xgFmglqU2XvO
coDHz442h71CD0 2iDVjQyO8Cmb87AmSc+dV4iXUalK5+GQRe21lAhIB2jVprdFvx6
VJvsF7Xf+RB 2GsZ61v4glGgYFaXLDeRYwyearjGuE2thLo9RdGu2/gfyJFwij43Lc
7kGX1/rI YHOTPJTmv5QQARAQABiQEfBBgBAgAJBQJXBQLPAhsMAAoJEFSQ7M+Lo56
EoLMH /3AMzxXON2m0rXwFVnBStaYGAC7bQilAJdgoiYASAxS2KHphpvHQ8Y6BUOHv
xG Wp4v350kZkiMGDblOe63/6mFHizFg/PTxeRDJLS7hWp1RUASd47hmBbrjFDRHu
4i1mYHrHvQy6QXSO6z88fStgYFWcer+JALtlnJCs8cQ67wMRxjZPEjUj1uGrm6 skK
Y5LBJvTCj4GN3vPVExvmLvRXPgS0pgiCYPdqbxUY97VT9jzsHXeCmmNJO8t oUnlH0
HpIcNfP76d3vdBwnAkCarnxqcCPBMZ+0lJWYUeqmlRTIBsIMRTOpTi3x fdbVBxlb+
wJ/p8VnJSURox3xoxHaJCHeU==jKED
-----END PGP PUBLIC KEY BLOCK-----Para comparar, o hash md5 (de 16 baites) da palavra “chave” em codificação hexadecimal (isto é, o alfabeto 0, …, 9, A, B, C, D, E, F) é
3fc75801d131d80c89186ce5d064dc2ba3.TSL])
A chave pública e privada podem inverter os seus papéis: Assim só o dono da chave privada pode cifrar o texto, e todo mundo (que conhece a chave pública) pode decifrá-lo.
O que parece fútil é com efeito um uso (economicamente) importantíssimo da criptografia assimétrica. Ele chama-se assinatura digital, e serve para identificar a fonte de dados na internet: Com efeito, como só o dono da chave privada pode cifrar o texto tal que a chave pública o decifre, todo mundo que conhece a chave pública pode verificar que o texto cifrado provém do dono da chave privada.
A criptografia assimétrica usa métodos matemáticos, mais exatamente aritmética modular, para cifrar. A segurança (= a dificuldade da decifração) da criptografia assimétrica é baseada em problemas matemáticos reconhecidos dificílimos há séculos.
A criptografia simétrica (como as funções de hash) usa métodos de cifrarão mais artesanais, que, de aparência, visam maximizar a difusão e confusão, principalmente por substituição e permutação (vide Seção 1.3.1). A segurança da criptografia simétrica é simplesmente baseada na renitência de falhar diante ataques de criptógrafos durante anos. Isto é, não é satisfatório de um ponto de vista transcendente, mais pelo menos prático. (A grande maioria das ciências, por exemplo, a medicina, confia quase exclusivamente nas estatísticas como fonte de conhecimento.)
O princípio de Kerckhoff postula que o
Enquanto o conhecimento da chave compromete uma única cifração, o conhecimento do algoritmo compromete todas as cifrações. Um algoritmo público garante a dificuldade da decifração depender só do conhecimento da chave, mas não do do algoritmo. Quanto mais usado, tanto mais provável que o algoritmo será conhecido. Para ele ser útil, necessita ser seguro mesmo sendo público.
As metas de Shannon da
desejam ofuscar a relação entre o texto cifrado e
Idealmente, quando uma letra da chave respectivamente do texto claro muda, a metade do texto cifrado mude, isto é, cada letra do texto cifrado mude com uma probabilidade de 50%. Enquanto a saída da cifração, o texto cifrado, depende deterministicamente da entrada, do texto claro, e da chave, o algoritmo visa ofuscar esta relação no sentido de torná-la tão complicada, entrelaçada, embaralhada quanto possível: cada letra da saída, do texto cifrado, depende de cada letra da entrada, do texto claro, e da chave.
Uma boa confusão ou difusão dificulta ataques estatísticos sobre
Textos claros geralmente não ocorrem com a mesma probabilidade. Ela depende, por exemplo, do idioma, do jargão ou do protocolo usado.
Moralmente, um método de criptografia é perfeitamente seguro se um texto cifrado gerado com ele não permite tirar conclusões sobre o texto claro correspondente. Isto é, a probabilidade que um texto claro e uma chave resultaram no texto cifrado é a mesma para todos os textos claros e todas as chaves.
Denote um texto claro e a sua probabilidade.
Um método de criptografia é chamado perfeitamente seguro se, para todo texto claro, a sua probabilidade é (estocasticamente) independente de qualquer texto cifrado. Em fórmulas, para todo texto claro e todo texto cifrado , temos .
Se um atacante interceptar um texto cifrado , então ele terá nenhuma vantagem, isto é, a sua probabilidade de obter o texto claro é a mesma como se ele não conhecesse .
Em 1949, Shannon provou o seguinte teorema, que explica sob quais condições um método de criptografia é perfeitamente seguro:
Seja finita o número de chaves e de texto claros e para todo texto claro . O método de criptografia é perfeitamente seguro, se
Isto é, desvios estatísticos tendem a enfraquecer o criptossistema. Em particular, é importante usar um gerador de números totalmente aleatório para as chaves.
Um criptossistema perfeitamente seguro é o one-time pad em que uma chave (do mesmo tamanho que o do texto claro) é adicionada (bite a bite) ao texto claro (vide ). Vide Seção 3.1.
Usar um tal criptossistema perfeitamente seguro é geralmente complicado na prática. Para aplicações em tempo real, como na Internet, eles são pouco usados.
Como segurança perfeita é inviável, a segurança é demonstrada
Embora existam criptossistemas simétricos comprovadamente seguros (tal como o gerador pseudo-aleatório de Blum-Blum-Shub cuja segurança é redutível ao problema da computação do Resíduo Quadrático), os algoritmos mais eficientes e mais usados, tal como o AES, comprovam a sua resistência apenas contra ataques conhecidos, tais como as da criptoanálise diferencial ou linear.
Os problemas usados pela criptografia assimétrica são todos NP: Todo algoritmo criptográfico cifra ou decifra uma mensagem com a chave em tempo polinomial no tamanho da chave em bites. Por outro lado, todos os algoritmos conhecidos para cifrar ou decifrar sem a chave levam tempo exponencial no tamanho da chave em bites.
Por enquanto, a conjectura sendo irresolvida, existem teoricamente algoritmos polinomiais para cifrar ou decifrar sem a chave em tempo polinomial; contudo, praticamente, após décadas de esforços contínuas da comunidade de criptógrafos em vão, parece improvável.
Exemplo. O exemplo inicial de um tal criptossistema comprovadamente seguro foi em 1982 o de Goldwasser e Micali para a segurança semântica pela redução ao problema do Resíduo Quadrático.
Dados e um produto de dois primos, é difícil determinar se é quadrático módulo (isto é, se existe tal que ou não) se, e tão-somente se, o assim-chamado símbolo de Jacobi para é e se os fatores primos de são desconhecidos.
O criptossistema de Goldwasser-Micali consiste em:
Logo em seguida, em 1985, surgiu criptossistema o algoritmo ElGamal, que foi provado semanticamente seguro pela redução ao problema de Diffie-Hellman Decisório. Isto é, a segurança semântica (IND-CPA) do criptossistema ElGamal é provada sob a hipótese da dificuldade do problema de Diffie-Hellman Decisório que é uma variação do (dificílimo) problema da computação do logaritmo discreto (na aritmética modular); vide Seção 6.2 para mais detalhes. Isto é, prova-se que ganhar o jogo do IND-CPA é pelo menos tão difícil quanto o problema de Diffie-Hellman suposições de segurança com um fator polinomial.
Cautela: A segurança teórica permanece uma idealização insuficiente para a realidade: Por exemplo, Ajtai e Dwork apresentaram em 1997 um criptossistema e o provaram teoricamente seguro pela redução a um problema difícil. Um ano depois, em 1998, este foi quebrado por Phong Nguyen e Jacques Stern.
O paradoxo é que comprovado não significa verdadeiro: um sistema comprovadamente seguro não é necessariamente verdadeiramente seguro, porque a prova se faz em um modelo formal que supõe
Por exemplo,
Além disto, a prova pode estar errada! Apesar desta incerteza, as provas de segurança são um critério (teoricamente necessário, mas praticamente insuficiente) útil para a segurança de um criptossistema.
O que exatamente significa segurança? A ideia que o atacante não pode derivar o texto original do texto cifrado é insuficiente, porque não significa que um atacante consiga outras informações relevantes sobre o conteúdo do texto claro (tais como trechos dele).
Mas até esta condição que não consiga informações sobre o texto claro é insuficiente nalgumas circunstâncias: Se
RSA de livro didático, por exemplo) eentão ele pode cifrar todos esses possíveis textos claros com a chave pública e comparar o texto cifrado com os seus textos cifrados obtidos.
Portanto, num método de criptografia assimétrica, sempre deve ser assumido que o atacante conheça a chave pública. Assim, ele pode cifrar qualquer texto claro de sua escolha e compará-lo com o texto cifrado para aprender algo sobre o texto claro desconhecido. Esse ataque é chamado de ataque de texto claro selecionado (Chosen Plaintext Attack = CPA).
Demarquemos a noção da segurança pela resistência contra vários cenários de ataques que ordenamos pelos recursos dos quais o atacante dispõe:
CPO = ciphertext-only attack)O atacante tem o texto cifrado de várias mensagens, todas cifradas pelo mesmo algoritmo. A tarefa do atacante é encontrar tantas mensagens claras quanto possíveis, ou melhor ainda, encontrar a chave ou chaves que foram usadas, o que permitiria decifrar outras mensagens cifradas com essas mesmas chaves.
O atacante tem o texto cifrado e supõe que o texto claro contenha certas palavras ou até frases inteiras (o crib). Por exemplo, a Enigma, máquina criptográfica usada pelos eixos de potências na Segunda Guerra Mundial, foi quebrada pela repetitividade das palavras nas mensagens; muitas comunicaram, por exemplo, diariamente o boletim meteorológico e o anunciaram por tais palavras (Wetterbericht em alemão) no início de cada tal mensagem.
KPO = known plaintext attack)O atacante tem o texto cifrado e o texto claro correspondente. A tarefa é encontrar as chaves usadas ou um algoritmo que decifra outros textos cifrados pelas mesmas chaves. (A criptoanálise linear situa-se neste cenário.) Um exemplo recente é um ataque de 2006 ao protocolo Wired Equivalent Privacy (WEP) para cifrar uma rede local sem fio que explora a previsibilidade de partes das mensagens cifradas, os cabeçalhos do protocolo 802.11.
CPA = chosen plaintext attack)O atacante tem o texto cifrado e o texto claro correspondente, e pode escolher os textos claros; assim que o atacante possa deliberadamente variar, ou adaptar, o texto claro e analisar as alterações resultantes no texto cifrado. (A criptoanálise diferencial situa-se neste cenário.)
Este é o cenário mínimo para criptografia assimétrica! Como a chave de criptografia é pública, o atacante pode cifrar mensagens à vontade. Logo, se o atacante pode reduzir o número de textos claros possíveis, por exemplo, ele sabe que são ou “Sim” ou “Não”, então ele pode cifrar todos os textos claros possíveis pela chave pública e compará-los com o texto cifrado interceptado. Por exemplo, o algoritmo modelar RSA (em Seção 8.1) sofre deste ataque, e nas suas implementações é preciso de preencher o texto claro por dados aleatórios para robustecê-lo contra este ataque CPA.
No ataque de texto cifrado selecionado o atacante seleciona diferentes textos cifrados (exceto o texto cifrado a ser decifrado) que serão decifrados para ele derivar a chave. Por exemplo, o atacante dispõe de um dispositivo que não é desmontável e cifra automaticamente.
No ataque de texto cifrado adaptativo os textos cifrados (exceto o texto cifrado a ser decifrado) são adaptados dependendo do texto obtido após cada decifração. Poucos ataques práticos se situam neste cenário, mas ele é importante para provas de segurança: Se a resistência contra os ataques neste cenário é comprovada, então a resistência contra todo ataque realístico de texto cifrado selecionado pode ser admitida.
O termo “segurança polinomial” apareceu em 1984 em Goldwasser e Micali (1984).
IND-CPAOs autores, Goldwasser e Micali, demonstraram subsequentemente que a segurança semântica é equivalente a IND-CPA, indistinguibilidade (IND) do texto cifrado sob texto claro selecionado (= Chosen Plain-text Attack):
Em um método de criptografia assimétrica, o atacante conhece a chave pública. Assim, ele pode cifrar qualquer texto claro de sua escolha e compará-lo com o texto cifrado para aprender algo sobre o texto claro desconhecido. Esse ataque é chamado de ataque de texto claro selecionado (CPA = Chosen Plain-text Attack). Um método de criptografia é seguro contra IND-CPA (indistinguibilidade do texto cifrado para textos claros selecionados), se nenhum atacante consegue distinguir o qual entre dois textos claros, que ele selecionou antes, corresponde ao texto cifrado, que recebeu depois.
O criptossistema é indistinguível sob ataque de texto claro selecionado se todo adversário de tempo polinomial probabilístico tiver apenas uma “vantagem” insignificante sobre adivinhação aleatória:
O jogo IND-CPA em quatro passos com restrição de tempo de execução polinomial (no comprimento [em bites] da chave ) para os cálculos de atacante (ao criar os dois textos claros, no segundo passo, e ao escolher o texto claro que corresponde ao texto cifrado, no quarto passo).
É criada um par de chaves, uma secreta e outra pública, ambas com bites. O atacante recebe a chave pública.
O atacante cria dois textos claros de tamanho igual e .
A máquina criptográfica
O atacante escolhe um bite em .
Um atacante que escolhe o bite na quarta etapa aleatoriamente está com probabilidade correto. Um método de criptografia é chamado seguro contra IND-CPA se nenhum atacante tiver uma probabilidade de sucesso significantemente maior que . Isto é, se é insignificante. O adversário tem uma “vantagem” insignificante, se vence com probabilidade , onde é uma função insignificante em , isto é, para toda função polinomial (diferente de zero) existe tal que para todo .
Uma diferença insignificante deve ser permitida porque é o atacante facilmente aumenta a sua probabilidade de sucesso acima de por adivinhar uma chave secreta e tentar decifrar o texto cifrado com ela.
Observação. Embora o jogo acima é formulado para um criptossistema assimétrico, pode ser adaptado ao caso simétrico, substituindo a cifração com a chave pública por um oráculo criptográfico (= uma função cujo funcionamento é totalmente desconhecido) que retém a chave secreta e cifra textos claros arbitrários a pedido do adversário.
Algoritmos de criptografia semântica segura incluem El Gamal e Goldwasser-Micali porque a sua segurança semântica pode ser reduzida à solução dalgum problema matemático difícil, isto é, irresolúvel em tempo polinomial; nestes exemplos, o problema Diffie-Hellman decisório e o Problema do Resíduo Quadrático. Outros algoritmos semanticamente inseguros, como RSA, podem ser tornados semanticamente seguros por preenchimentos criptográficos aleatórios como o OAEP (= Optimal Asymmetric Encryption Padding).
Exemplo. O método de criptografia Elgamal é IND-CPA-seguro sob a hipótese de que o problema de Diffie Hellman Decisório seja difícil. Para provar a segurança, construamos a partir de um
IND-CPA para El Gamal (isto é, se lhe é dada a cifração de uma de duas mensagens claras sob a chave pública, então ele identifica com probabilidade à qual (das duas mensagens claras) ela corresponde),DDH, isto é, dada uma base e expoentes , e em , decide em tempo polinomial se ou não,como se segue:
A estratégia de é, portanto, optar por se, e tão-somente se, está correto. Logo, a probabilidade que esteja correto é .
IND-CCARecordemo-nos de
IND-CPA (indistinguibilidade de texto cifrado para textos claros selecionados), se nenhum atacante consegue distinguir o qual entre dois textos claros, que ele selecionou antes, corresponde ao texto cifrado, que recebeu depois, eUm método de criptografia é seguro contra IND-CCA (indistinguibilidade de texto cifrado para textos cifrados selecionados), se o atacante, no segundo e quarto passo do jogo de IND-CPA, pode mandar decifrar qualquer texto cifrado (exceto aquele a ser decifrado), e, mesmo assim, não consegue distinguir o qual entre dois textos claros corresponde ao texto cifrado:
Exemplo. O ataque de Bleichenbacher de PKCS#1 de 1998 contra a variante de RSA seguro contra IND-CPA (mas, justamente, não contra IND-CCA).
Bellare e Namprempre mostraram em 2000 para uma cifra simétrica que se
IND-CPA, eentão a cifra com Encrypt-then-MAC resiste contra um ataque IND-CCA.
Um sistema criptográfico é maleável se é possível transformar toda mensagem cifrada de uma mensagem , sem nenhum conhecimento sobre , em uma mensagem cifrada de alguma mensagem por uma função conhecida tal que a relação entre e seja conhecida.
Exemplo. Todos os criptossistemas comuns são maleáveis; veremos, entre outros, que o criptossistema ElGamal é maleável.
Como consequência prática, uma cifra maleável não permita verificar a autenticidade de uma mensagem, isto é, se foi alterada entre envio e receção. Logo, é mais suscetível a um ataque de Man-in-the-middle, um homem (no meio) entre dois correspondentes que interceta e forja as suas mensagens trocadas.
Se a maleabilidade é indesejada (para garantir a autenticidade da mensagem cifrada), então se anexa à mensagem um valor de uma função unidirecional, tal como um hash criptográfico, chamado de Código de Autenticação de Mensagem (MAC) da mensagem cifrada. (Chamado de Encrypt-then-MAC e usado, por exemplo, em VPNs, redes privadas virtuais. O hash não cifrado da mensagem clara, MAC-and-Encrypt é usado no protocolo SSH e o hash cifrado da mensagem clara no protocolo TLS que segura o protocolo HTTPS.) Embora um atacante possa alterar a mensagem cifrada , não consegue alterar o seu MAC.
Observação. Existem cifras assimétricas não-maleáveis; a primeira tal cifra foi a de Cramer-Shoup.
O one-time pad que
é maleável porque um bite no texto cifrado é invertido se, e tão-somente se, o bit correspondente no texto claro é invertido.
Se o atacante sabe decifrar um trecho do texto cifrado, então ele pode alterá-lo para corresponder a qualquer outro texto do mesmo comprimento. Isto é: Se seja o texto claro, a chave secreta e o texto cifrado, então o texto cifrado de para qualquer é .
No sistema criptográfico RSA, um texto claro é cifrado por onde é a chave pública módulo . Se é um texto cifrado de um texto claro , então o texto cifrado de para qualquer é Por isso, quando implementado, o texto claro é primeiro preenchido aleatoriamente por um protocolo como OAEP ou o PKCS1.
No sistema criptográfico ElGamal, um texto claro é cifrado pelo par , onde é a chave pública para a base . Logo, se o par é o texto cifrado de , então, para qualquer , o par , é o texto cifrado de .
É recomendado experimentar com o aplicativo CrypTool que
apresenta mais de algoritmos criptográficos tais como os históricos (simétricos)
Enigma,mas também os modernos simétricos e assimétricos, como
AES, eRSAe
Além disto, explica a matemática por trás destes algoritmos, por exemplo, o Algoritmo de Euclides, por animações.
Tem duas versões diferentes, CrypTool 1 e CrypTool 2. Trabalhamos de preferência com o CrypTool 1.
CrypTool 2Apresentamos uns exemplos antigos de algoritmos criptográficos sobre textos: Historicamente, a criptografia estuda a transformação de um
tal que só uma informação adicional secreta, a chave, permita desfazê-la.
Os algoritmos protótipos históricos são
Veremos que mesmo com a presença de muitas chaves um algoritmo, como o dado pela permutação arbitraria do alfabeto que tem quase chaves, pode ser facilmente quebrado porque preserva regularidades como a da frequência das letras.
Como critério suficiente para uma boa segurança existe o da boa difusão por Shannon: Idealmente, se uma letra do texto claro muda, então a metade das letras do texto cifrado muda.
Veremos em Seção 3 como os algoritmos modernos, as redes da substituição e permutação, juntam e iteram os dois algoritmos protótipos complementares para atingir a meta da boa difusão por Shannon.
Este método foi usado por (Júlio) César (100 – 44 B.C.) e por Augusto (César) (63 – 14 B.C.): Fixa-se uma distancia entre letras em ordem alfabética, isto é, um número entre 0 e 25, e traslada-se (para frente) cada letra do alfabeto (latino) por esta distância . Suponhamos que as letras sejam arranjadas em um anel; assim que o traslado de uma letra no fim do alfabeto resulte em uma letra no início do alfabeto.

Por exemplo, se , então
Existem chaves (incluindo a chave trivial ).

Para decifrar, traslada-se cada letra pela distância , isto é, posições para trás. Se as letras do alfabeto forma uma roda, então as letras estão trasladadas
Pela ciclicidade (ou circularidade) da formação das letras, observamos que um traslado de posições no sentido anti-horário iguala a um de posições no sentido horário.
Questão: Para qual a cifração é auto-inversa, isto é, a cifração iguala a decifração?
Em vez de substituirmos cada letra por outra trasladada pela mesma distância fixada , substituamos cada letra por outra letra arbitrária, por exemplo:
| A | B | … | Y | Z |
| … | ||||
| E | Z | … | G | A |
Para podermos desfazer a cifração, é necessária que nunca duas letras sejam enviada a mesma letra! Isto é, permutamos as letras. Assim obtemos chaves ( o número de senhas que podem ser formados com bites).
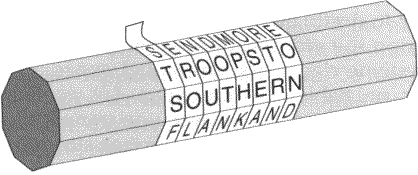
A cítala ou o bastão de Licurgo (= legislador de Esparta cerca de 800 AC) é um bastão com o qual os espartanos cifravam como segue:
As letras assim transpostas no pano podiam unicamente ser decifradas por um bastão com a mesma circunferência (e suficientemente comprido) pela mesma maneira como o texto foi cifrado:

Aqui, a chave é o número dado pelo número das letras que cabem nesta circunferência.
Por exemplo, se o bastão tem uma circunferência de letras (e um comprimento de letras), as duas linhas
| l | u | a |
| m | e | l |
tornam-se as três linhas
| l | m |
| u | e |
| a | l |
que são concatenadas (para não revelarem nem a circunferência, nem o comprimento) à linha
| L | M | U | E | A | L |
Aplicamos os critérios para segurança em Seção 1.3.1 aos exemplos históricos.
A Substituição (das letras do alfabeto por traslado) usada por César
viola todas as qualidades desejáveis, principalmente o princípio de Kerckhoff, que o algoritmo seja público:
Uma vez o método for conhecido, considerando a pequena quantidade de 25 chaves, o texto cifrado cede em pouco tempo a um ataque de força bruta, uma busca exaustiva que prova cada chave.
A Substituição (das letras do alfabeto por permutação arbitrária)
| A | B | … | Y | Z |
| … | ||||
| E | Z | … | G | A |
tem chaves, por isso um ataque de força bruta é computacionalmente inviável.
Mas ele viola as metas da difusão e confusão. Se a chave (= permutação do alfabeto) troca a letra pela letra , então há
Com efeito, o algoritmo permite ataques estatísticos sobre a frequência de
em português. Por exemplo,
Substituindo
é um ponto de partida propício para decifrar o texto: Quanto mais texto cifrado, tanto mais provável que esta substituição coincide com a dada pela da chave para estas letras.
Por exemplo, o texto considerando que as três letras mais comuns do português são, nesta ordem, AEO e que , e aparecem respectivamente , e vezes, obtemos Suponhamos que = e que = . Em particular, corresponde a e a . Logo para estarmos levados ao chute Este exemplo é muito artificial pela sua brevidade que dificilmente permita formar uma frase que tenha no mesmo tempo um conteúdo típico e frequências de letras típicas. Como exercício, caro leitor, construa uma tal frase!
A cítala viola
Com efeito, o valor máximo da circunferência é onde = o número das letras do texto cifrado. Por isso, um ataque de força bruta, é viável.
Ela tem
Com efeito, o algoritmo permite ataques estatísticos sobre a frequência de
Por exemplo, propício seria a escolha da circunferência como o número que maximiza a frequência do bigrama ‘de’ entre as cadeias de letras nas posições , .
Por exemplo, se olhamos observamos que e são distanciados por três letras, o que nos leva ao chute que e à decifração
A enigma substitui o alfabeto, isto é, permuta as letras do alfabeta latim, mas cada letra por outro alfabeto; é uma substituição poli-alfabética.
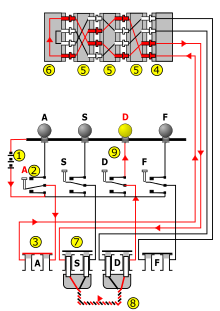
O esquema elétrico, constituído por:
Ao teclar uma letra, a corrente entra
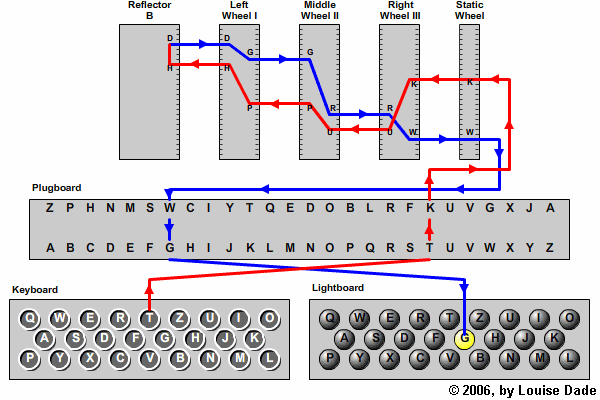
Cada cilindro consiste em
Ao teclar uma letra, o rotor à direita (o rotor rápido) avança uma posição (antes da corrente entrar nos cilindros). Figura 2.1 mostra a substituição da letra A
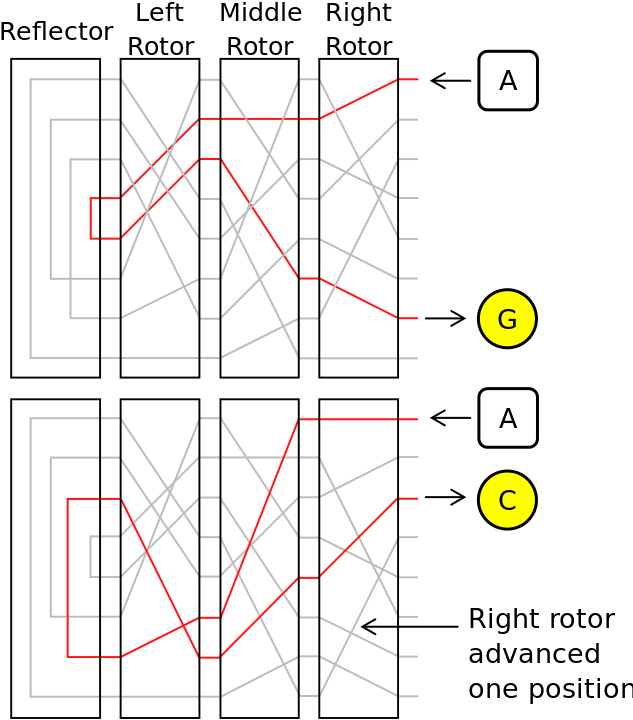
Em posições inicialmente determinadas pela posição do anel do rotor rápido e do rotor no meio, avançam também, uma posição,
Após este primeiro avanço (ou do rotor médio, ou do rotor lento),
Isto é, os rotores comportam-se como os de um taxímetro ou conta-quilômetros, com a diferença que
(além do detalhe que o rotor médio avança mais uma vez após o avanço do rotor lento). Esta simulação da Enigma online mostra a cifração da Engima em ação.
Cada cilindro permuta o alfabeto inteiro por um cabeamento interno. Este cabeamento é fixo, e não pode ser mudado pelo usuário. Por dentro, há uma verdadeira salada de cabos:

O anel tem o entalhe que desencadeia o avanço do rotor seguinte. Por isso, a posição do anel determina o ponto em que o vai-um, o avanço do rotor seguinte, tem lugar. Como o rotor lento não tem sucessor, de fato só as posições do rotor médio e rápido têm efeito criptográfico.
O cilindro de retorno garante que a substituição seja auto-inversa, isto é, a cifração iguale à decifração. Também, um defeito criptográfico, implicou que uma letra nunca foi cifrada a si mesma para evitar um curto-circuito!
O cilindro de entrada igualmente permuta o alfabeto, mas só existia na versão comercial da Enigma.

Na versão militar, não fazia nada, isto é, a substituição é a identidade. Isto foi intuído por Marian Rejweski, criptógrafo polonês (pelo vício dos alemães na ordem) antes da Segunda Guerra Mundial. Assim conseguiu inferir o cabeamento dos cilindros da Enigma à distância, enquanto os franceses e britânicos estavam perdidos.
O painel de ligações troca uns pares de letras, na prática, dez. Por exemplo, na foto, A e J, e S e O.

Expresso por uma fórmula, a substituição (= Maquina) da Enigma descreve-se pela concatenação das substituições onde
O CrypTool 2 inclui uma animação do funcionamento criptográfico da Enigma. (Mencionamos que o funcionamento do anel é errôneo, porque não afeta o momento do vai-um.)

CrypTool 2Em particular, como a cada letra teclada (ao menos) o rotor rápido avança uma posição, isto é é aumentado por , toda a substituição muda. (E a cada rotação completa do rotor rápido, após 26 avanços, o rotor médio avança, e igualmente, a cada rotação completa do rotor médio, após 26 avanços, o rotor lento avança.)
Como a cada letra teclada o rotor rápido avança uma posição,
Por isso, as mesmas substituições só reaparecem após uma rotação completa de todos os cilindros, em particular, do cilindro lento; isto é, após cerca de tecladas (a periodicidade). A Enigma é uma cifração por uma substituição poli-alfabética.
Recordemo-nos de que o ataque estatístico pelas frequências das letras
Esta correspondência entre a frequência da letra cifrada e a da letra clara necessita que cada letra seja substituída pela mesma substituição!
Logo, o ataque estatístico pela frequência das letras (por exemplo, da língua alemã) para decifrar o texto,
1, 17.001, 34.001 e assim por diante são substituídas pela mesma substituição); por exemplo, em um texto com letras, um livro espessíssimo;Para a Engima I, há quatro fatores:
Ordem e Escolha dos Cilindros: Foram escolhidos (o lento, no meio e o rápido) entre cilindros e em qualquer ordem, resultando em possibilidades.
Posição do Anel: Determina a qual ponto o cilindro seguinte inicialmente avança uma posição, isto é, quando a rodada inicial se completa. Depois, uma rodada se completa a cada letras. Há posições ( – ) do anel para o rotor rápido e no meio (enquanto a posição do anel do rotor lento não importa, porque não implica um avanço de um cilindro em seguida), resultando em possibilidades.
Posição do Rotor: Determina em qual ponto a corrente inicialmente entra. Para cada um dos rotores, há possíveis posições ( – ), resultando em posições. Por causa do mecanismo do escalonamento, posições entre elas são criptograficamente redundantes, sobrando possibilidades.
Conexões do Painel: Há até cabos com dois conectores para conectar as letras do alfabeto.
Em geral, para o cabo , há possibilidades.
Como a ordem em que os pares de letras foram conectadas pelos cabos não importa, divide-se por .
Ao total, obtemos possibilidades. Durante a guerra, a partir de Agosto 1939, foram conectados pares de letras, dando possibilidades.
Resumimos que há
o que dá ao total possibilidades, mais o menos o número de sequências de bites. (Por exemplo, o DES (= Data Encryption Standard) utiliza uma chave de bites.)
Na Segunda Guerra Mundial as mensagens enviadas pelos alemães tiveram, por ordem, no máximo letras. Por isso:
Logo, importam criptograficamente
A bomba de Turing ajudou a reduzir estas possibilidades, sobretudo as do maior fator, as ligações do painel. Sobraram ainda possibilidades. Considerando a força de trabalho de pessoas (entre elas mulheres) em Bletchley Park, o centro criptográfico inglês, neste ponto, um ataque de força bruta é viável, isto é, provando exaustivamente todas as possibilidades sobrantes.

Presumindo uma configuração do painel de ligações e um crib, uma palavra (alemã típica) que provavelmente ocorre no texto cifrado, a bomba de Turing (o nome deriva-se do som de uma bomba-relógio que a primeira tal máquina, a bomba criptográfica polonesa, emitia) elimina muitas posições de cilindros inválidas, da seguinte maneira:
Intui um crib, uma palavra provável, por exemplo,
OBERKOMMANODERWEHRMACHT, (= comando supremo do exercito alemão)WETTERBERICHT (= previsão do tempo)EINS (= o número um)e compara com um trecho do texto cifrado. Para encontrar o trecho certo, toma em conta que a Enigma nunca cifrava uma letra a si mesma!
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| W | E | T | T | E | R | B | E | R | I | C | H | T |
| A | R | E | S | T | U | W | L | S | K | H | I | O |
Cria o menu, um diagrama do percurso de uma letra dado pelas substituições entre o texto claro e o texto cifrado; aqui obtemos o circuíto
| R | — | 2 | — | E |
| 9 | 3 | |||
| S | — | 4 | — | T |
Isto é, são trocadas as letras
Intui um conector do painel de ligações que troca uma das letras do circuito, por exemplo a troca entre e .
Então, a Bomba de Turing, fixados
WETTERBERICHT,ARESTUWLSKHIO, eprovou cada posição de cilindros para a sua compatibilidade com os circuitos do menu, da seguinte maneira:
Recordemo-nos de que a substituição da uma letra pela Enigma se descreve pela concatenação das substituições seguintes onde
Para facilitar,
Isto é,
Para destacar a dependência da substituição da posição da letra no texto a ser cifrado (pelo avanço do cilindro rápido a cada letra teclada), denote (Conforme à notação anterior e supondo que o cilindro no meio não avance, ela deveria ser onde é a configuração inicial do cilindro lento, médio e rápido.) Aqui para , obtemos Como o painel de ligação troca as letras em pares, a substituição pelo painel de ligação é auto-inversa, isto é, . Por isso, ao aplicarmos a ambos lados desta equação, Em seguida, da mesma maneira, e assim por diante para as outras letras no circuito, até fechando o circuito.
Isto é, sob esta configuração dos cilindros, obtemos que a substituição deixa a letra invariante,
Concluímos que cada tal circuito (obtido pelo texto claro e cifrado) exclui muitas configurações. A Bomba calculou quais.
Alan Turing calculou quantas configurações de posições de cilindros são em média compatíveis para um Crib com dado número de circuitos e letras :
| # circuitos \ # letras | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|
| 3 | 2.2 | 1.1 | 0.42 | 0.14 | 0.04 | <0.01 | <0.01 | < 0.01 |
| 2 | 58 | 28 | 11 | 3.8 | 1.2 | 0.30 | 0.06 | < 0.01 |
| 1 | 1500 | 720 | 280 | 100 | 31 | 7.7 | 1.6 | 0.28 |
As equações acima implicam também, a partir de
todas as outras trocas das letras no circuito pelo painel de ligações:
Por exemplo, dado , o valor define-se por em seguida, e assim por diante, obtendo as trocas de todas as letras do circuito: , , e .
Como a validade da chave era um dia, e a mesma entre todas as naves (e entre todas as aeronaves e entre todos os trens), logo que uma chave foi obtida, todas as mensagens entre todas as naves durante este dia podiam ser decifradas com ela. Mudavam as posições dos rotores e conectores do painel cada dia, e a escolha e ordem dos cilindros cada mês.
Destacamos a importância do crib, da palavra alemã típica, neste método. Os aliados até provocaram pelas suas manobras certas mensagens para aplicar este método. Caso contrário, não conseguiram por exemplo decifrar a comunicação entre os condutores de trem por desconhecimento do jargão (= gírias profissionais) entre eles.
Hoje em dia, a criptografia estuda a transformação de
tal que só uma informação adicional secreta, a chave, permite desfazê-la.
| dados | = | arquivo digital (de texto, imagem, som, vídeo, …) |
| = | sequência de bites (= 0, 1) | |
| = | sequência de baites (= 00, 01, …, FE, FF) | |
| = | número (= 0, 1, 2, 3 …) |
O One-time pad (= Bloco de Uso Único) adiciona (pela operação XOR, isto é, ou exclusivo, a disjunção exclusiva) cada baite do texto claro com o baite (na posição) correspondente de uma chave que
Isto é, o texto cifrado é Este método de cifração é tão seguro quanto teoricamente possível!
Se o texto claro tem um único bloco , então a simples adição (XOR) de uma chave, o one-time pad, é um algoritmo seguro. Porém, é frequentemente inconveniente ou até praticamente impossível ter uma chave tão grande quanto o texto claro: Por exemplo,
Na prática, imagine-se um agente duplicar gigabaites de ruído em dois meios de armazenamento, por exemplo, um disco rígido e pendrive, e levar um destes meios para cifrar a sua comunicação pelo one-time pad.
Infelizmente, é uma péssima ideia (apesar de ser tão natural) de usar a mesma chave para dois blocos diferentes: se, por exemplo, o texto claro tem dois blocos e , então, com este algoritmo, a soma (XOR) dos dois blocos cifrados e iguala a soma dos dois blocos claros (porque a adição XOR é por definição auto-inversa, isto é independente do dígito binário ser ou )!

Pode ser visto como a cifração do primeiro bloco por one-time pad cuja chave é o segundo bloco. Infelizmente, o segundo bloco não é uma boa chave, porque longe de ser aleatório; ao contrário, normalmente o seu conteúdo semelha ao do primeiro bloco, isto é, a chave é previsível.
Por isso, é mais seguro aplicar uma substituição do bloco por outro segunda a escolha da chave.
Porém, o alfabeto desta substituição seria gigantesco, e, por isso, este ideal é praticamente inatingível, sobretudo sobre um hardware tão limitado quanto o de um cartão inteligente com o seu processador de bites.
Para um bloco de por exemplo, baites, esta tabela de substituição teria horrendos baites. Por isso, por exemplo, o AES adiciona a chave; depois substitui só cada baite, cada casa do bloco, uma tabela de substituição de entradas de baite; em seguida, permuta as casas. Veremos que estas operações se complementam tão bem que são quase tão seguros como uma substituição do bloco inteiro. Isto é, em compensa da ausência de uma substituição do bloco inteiro por outro, a permutação imita esta substituição gigantesca da melhor maneira.
Uma Cifra de Feistel ou uma rede de substituição e permutação (abreviada SPN para Substitution Permutation Network) agrupa o texto (= sequência de baites) em blocos de baites (por exemplo, para AES e no nosso modelo prototípico) e cifra cada bloco pela iteração (por exemplo, vezes no AES, e vezes no nosso modelo prototípico) dos três seguintes passos, em dada ordem:
XOR) da chave,Isto é, após
One-time pad,são aplicadas
AES cada baite, par de letras hexadecimais, por outro), eAES, que agrupa o texto em um quadrado de baites (= pares de letras hexadecimais), são permutas as casas nas linhas (e colunas).Estas duas simples operações,
complementam-se muito bem, isto é, geram alta confusão e difusão após de poucas iterações.
Na primeira e última rodada, os passos antes respetivamente depois da adição da chave são omitidos porque não aumentam a segurança criptográfica: Como o algoritmo é público (segundo o critério de Kerckhoff), qualquer atacante pode desfazer os passos que não necessitam o conhecimento da chave.
Usamos o algoritmo de Heys (2002) como modelo simples de uma cifra de Feistel que
e em cada uma das primeiras rodadas , e ,
Adiciona a chave da rodada (para cada rodada, tem uma chave correspondente independente) ao bloco, .
Substitui cada um dos sub-blocos de bites pela tabela
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 4 | D | 1 | 2 | F | B | 8 | 3 | A | 6 | C | 5 | 9 | 0 | 7 |
Troca o bite do sub-bloco com o bite do sub-bloco ;
Na penúltima rodada
Na última rodada
Isto é:
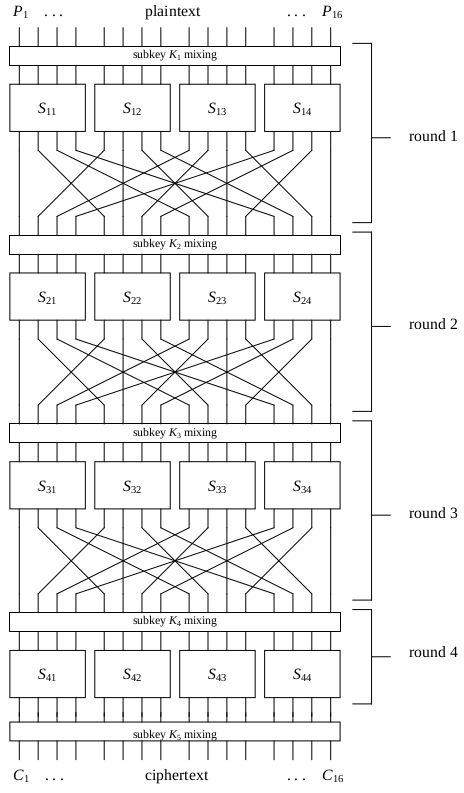
A tabela origina do algoritmo DES e e comumente chamada de S-box, caixa de substituição.
Para compreender as razões por trás das escolhas de cada passo de um algoritmo criptográfico simétrico moderno que cifra em blocos, tal como o AES, precisa-se de entender contra quais ataques se robustece. Um dos mais conhecidos ataques é o da criptoanálise diferencial que vamos explicar agora pelo exemplo da cifra de bloco prototípica de Heys:
O sonho de todo decifrador é poder aprender se uma parte da chave escolhida é correta, isto é, se coincide com a parte correspondente da chave usada para cifrar o texto: Por exemplo, no algoritmo de Heys a chave consiste de bites: Se for possível saber, para bites da chave provada, se eles coincidem com os bites correspondentes da chave correta, então o decifrador
Isto é, o número de combinações que precisam ser provadas foi reduzido de a .
Mais exatamente, a chave consiste de blocos de bites. Daremos um exemplo da criptoanálise abaixo em que o decifrador terá um critério probabilista para decidir se dos blocos, isto é, bites, da chave provada são corretos.
No ataque de força bruta, o decifrador, para cada chave possível, decifra o texto cifrado com ela. Para saber se a chave é correta, isto é, se coincide com a chave usada para cifrar o texto, o decifrador verifica se o conteúdo seja inteligível; por exemplo, pelo critério de
Se a cifra tem uma única rodada, então este critério se aplica. Porém, se a cifra tem duas ou mais rodadas, e o decifrador executa a última rodada do algoritmo da decifração com certa chave, então este critério não presta mais porque o texto obtido é a saída do algoritmo da cifração (com a mesma chave) da penúltima rodada (logo, de qualquer forma, ininteligível). Ao invés dele, o critério da criptoanálise diferencial para ter encontrado a chave correta é probabilista: a chave provada é provavelmente correta se, para uma determinada diferença “entrante” e uma determinada diferença “sainte” , pares de textos claros com diferença resultam na penúltima rodada com determinada probabilidade em pares de textos cifrados com diferença .
Para a criptoanálise diferencial ser aplicável, o decifrador precisa de poder cifrar pelo cifrador (pela mesma chave)
em seguida,
A criptoanálise diferencial explora a alta probabilidade da propagação de uma diferença entre dois textos claros e a uma diferença entre os dois textos cifrados e de e na penúltima rodada. (Recordemo-nos de que é a adição XOR bite a bite, em que a saída é se, e tão-somente se, as duas entradas são diferentes. Isto é, , indica todos os bites em que e diferem.)
Chamemos este par o diferencial. Para a criptoanálise diferencial ser eficiente, é preciso existir um diferencial com alta probabilidade (onde alto é quantificado em Equação 3.1); isto é, entre todos os pares entrantes com a diferença , a probabilidade de um par sainte ter diferença (na penúltima rodada) é . Mais exatamente, o cifrador cifrará um número estatisticamente significante de pares () de textos claros com diferença para contar o número de pares dos textos cifrados com diferença .
Observemos que para uma aplicação afim (isto é, dada por um polinômio de grau , ou, equivalentemente, a composição
o diferencial independe do par e entrante: Se a aplicação
Aplicada esta observação à uma cifre de Feistel, vemos que
isto é, a diferencial independe do par e entrante. Porém, a diferença sainte da substituição não é determinada apenas pela diferença , mas ela depende de e !
Logo, para encontrar tal diferencial com uma alta probabilidade , precisamos de investigar apenas a tabela de substituição. Estamos interessados na frequência de uma diferença sainte dada uma diferença entrante : Dada , há possibilidades para (e o qual determina ), e contamos as frequências das possíveis saídas .
Esta tabela alista, para umas diferenças entrantes e todos os pares entrantes com estas diferenças, as suas diferenças saintes.
Contemos, para toda diferença entrante , quantas vezes cada diferença sainte resulta entre todos os possíveis pares entrantes e com .
| $backslash | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 2 | 4 | 0 | 4 | 2 | 0 | 0 |
| 2 | 0 | 0 | 0 | 2 | 0 | 6 | 2 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 |
| 3 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 4 | 2 | 0 | 2 | 0 | 0 | 4 |
| 4 | 0 | 0 | 0 | 2 | 0 | 0 | 6 | 0 | 0 | 2 | 0 | 4 | 2 | 0 | 0 | 0 |
| 5 | 0 | 4 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 2 |
| 6 | 0 | 0 | 0 | 4 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 2 | 2 |
| 7 | 0 | 0 | 2 | 2 | 2 | 0 | 2 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 4 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 4 | 0 | 4 | 2 | 2 |
| 9 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 4 | 2 | 0 | 2 | 2 | 2 | 0 | 0 | 0 |
| A | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 2 | 0 | 0 | 4 | 0 |
| B | 0 | 0 | 8 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 2 |
| C | 0 | 2 | 0 | 0 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 6 | 0 | 0 |
| D | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 4 | 2 | 0 | 2 | 0 | 2 | 0 | 2 | 0 |
| E | 0 | 0 | 2 | 4 | 2 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| F | 0 | 2 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 4 | 0 | 2 | 0 | 0 | 2 | 0 |
As entradas de cada linha somam-se a , o número dos possíveis pares para uma dada diferença entre eles. A primeira linha constata que duas entradas iguais resultam em duas saídas iguais. O número maior é e atingido para e . Além dele, surge cinco vezes o número .
Exemplo. A tabela de frequência
Escolheremos os nossos diferenciais entre os com estas altas frequências:
Para uma cifra de Feistel, uma trilha diferencial é uma sequência finita de diferenças tal que toda diferença é a entrada da S-box da rodada da cifra. Dada a saída da S-box da rodada , a entrada da rodada seguinte é o resultado da aplicação da permutação a .
Queremos encontrar o mais provável trilha diferencial da cifra de Heys, ou, pelo menos, tal que cada diferencial seja entre os mais prováveis.
Todo diferencial consiste de sub-diferenciais, correspondente aos sub-blocos de bites que constituem o bloco de bites. Para encontrar uma tal trilha diferencial provável, queremos, em cada rodada,
S-box substitui a diferença entrante pela diferença sainte do sub-diferencial;Um exemplo de uma tal trilha é a seguinte: Seja a diferença entrante na primeira rodada que é pela S-box substituída por Pela permutação subsequente, obtemos a diferença entrante na segunda rodada que é pela S-box substituída por Pelos bites número e diferentes de zero, obtemos na terceira rodada pela permutação a diferença entrante com dois sub-diferenciais ativos que é pelas S-boxes e substituída por Finalmente, obtemos pela permutação como entrada da quarta rodada
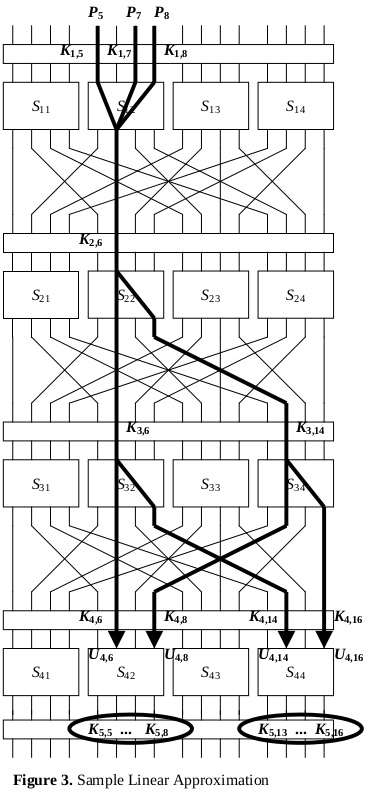
Denote a substituição do sub-bloco pela S-box na rodada . Na nossa trilha diferencial, alistamos
a probabilidade que, se a diferença entre na substituição , então a diferença saia:
| Substituição | Entrada | Saída | Probabilidade |
|---|---|---|---|
Se suponhamos que os diferenciais de uma rodada sejam independentes dos diferenciais da rodada anterior, então a probabilidade da substituição por é o produto das probabilidades de cada substituição,
A fim de encontrar a chave, para
o decifrador
S-box na quarta rodada pela chave para obter o par e e assim a diferença , eSe para uma combinação de sub-blocos e vale , isto é, a proporção entre
é próxima da probabilidade , então estes sub-blocos são provavelmente os sub-blocos e da chave usada pelo cifrador.
Observação. Para concluir ter encontrado os sub-blocos corretos, usamos as hipóteses
Os dois não tem fundamento matemático rígido, mas são apenas plausíveis, porque, respetivamente:
Notemos que para este ataque ser mais rápido, isto é, ser mais eficaz do que o ataque de força bruta (que simplesmente prova todas as chaves possíveis), é preciso onde
Logo, é necessário que a trilha seja estreita, isto é, tenha poucos blocos ativos, para poder aprender se a chave provada é correta, isto é, coincide com a chave usada, apenas nestes blocos ativos (o que reduz o número de combinações logaritmicamente). No exemplo dado, apenas dos sub-diferenciais são ativos, o que permitiu ao decifrador aprender nestes blocos se a chave é correta: o número de combinações que precisam ser provadas foi reduzido de a .
AESOs algoritmos criptográficos simétricos modernos, tais como DES e AES, cifram dados em vez de textos, isto é, sequências de baites ou bites. Ambos, o DES e o AES, são cifras de bloco, isto é, agrupam o texto claro em blocos de um tamanho de baites determinado (no caso do AES, de , ou baites).
Lembremo-nos de que, idealmente, a rodada consistiria só
Porém, o alfabeto desta substituição seria tão gigantesco que este ideal é praticamente inatingível; sobretudo sobre um hardware tão limitado quanto o de um cartão inteligente.
Para um bloco de por exemplo, baites, esta tabela de substituição teria horrendos baites. Por isso o AES substitui só cada baite, cada casa do bloco, uma tabela de substituição de entradas de baite; em seguida, considera o bloco como quadrado de casas, e
Os criadores do AES conseguiram demonstrar em Daemen e Rijmen (1999) que estas duas operações se complementam tão bem que, após várias iterações, quase compensam da ausência de uma substituição do bloco inteiro por outro. Isto é, conseguiram demonstrar que é imune contra um ataque de criptoanálise diferencial em Seção 3.4 pela sua ótima difusão. Para uma fonte mais detalhada, vide Daemen e Rijmen (2002).
Em vez disto, para conseguirem uma boa confusão e difusão (como definidas por Shannon), iteram ambas as operações (conhecidas pelos algoritmos antigos que operam sobre textos),
além da operação (nova sobre dados = sequências de bites),
O algoritmo AES é o vencedor de uma competição anunciada pelo National Institute of Standards and Technology of the United States (NIST) de 1997 a 2000 para substituir o então padrão de criptografia simétrico, o Data Encryption Standard (DES).
Antes de tornar-se o AES, este algoritmo foi denominado pelos seus criadores Vincent Rijmen e Joan Daemen Rijndael, pelas letras iniciais dos seus sobrenomes.
No final da competição, restaram estes cinco algoritmos com as seguintes votações:
Rijndael: 86 votos positivos, 10 negativosSerpent: 59 votos positivos, 7 negativosTwofish: 31 votos positivos, 21 negativosRC6: 23 votos positivos, 37 negativosMARS: 13 votos positivos, 84 negativosEntre eles, nenhum deles se destacou pela sua maior segurança, mas o Rijndael, sim, pela sua simplicidade, ou clareza, e em particular economia computacional, na implementação. Como este algoritmo será a rodar por toda parte, por exemplo, nos processadores minúsculos de 8 bites nos cartões inteligentes (smartcards), a decisão foi tomada em favor do Rijndael.
Até hoje, este algoritmo continua firme e forte e é considerado o mais seguro; não há necessidade para outro padrão de algoritmo criptográfico simétrico.
E com efeito roda em todo lugar. Por exemplo, para cifrar uma rede sem fio, usa-se uma chave só, então a criptografia é simétrica. A opção mais segura, e logo mais recomendada, é a cifração por AES.
AESVamos conhecer este algoritmo tão simples!
O algoritmo AES agrupa o texto claro (e as chaves) em retângulos de baites onde Comumente, e para nós de agora para diante, , isto é, os retângulos são quadrados. Em base hexadecimal (= cujos algarismos são – , , , , , e ), um tal quadrado tem por exemplo a forma
| A1 | 13 | B1 | 4A |
| A3 | AF | 04 | 1E |
| 3D | 13 | C1 | 55 |
| B1 | 92 | 83 | 72 |
RijndaelNão para implementá-lo, mas para entendermos as funções do AES, principalmente SubBytes e MixColumn, precisamos de uma digressão matemática: Um baite em é considerado como polinômio com coeficientes binários por Por exemplo, o número hexadecimal , ou baite , corresponde a
Todas as adições e multiplicações têm lugar no corpo binário com elementos, o qual é um conjunto de números com uma adição e multiplicação (que satisfaz a leis comutativa, associativa e distributiva; como, por exemplo, ) construído como segue: Seja o corpo de dois elementos com
XOR), e asSeja isto é, as somas finitas para , , …, em e seja Isto é, o resultado de ambas as operações e em é o resto da divisão por .
A adição de dois polinômios é a adição em coeficiente a coeficiente. Isto é, como baites, a adição é dada pela adição XOR.
A multiplicação é dada pela multiplicação natural seguida pela divisão com resto pelo polinômio Por exemplo, em notação hexadecimal, , pois e
A multiplicação pelo polinômio não muda nada, é o elemento neutro. Para qualquer polinômio , o algoritmo estendido de Euclides, calcula polinômios e tais que Isto é, na divisão com resto de por sobra o resto . Quer dizer, é o inverso multiplicativo em , Quando invertermos um baite em , referimo-nos ao baite .
Com efeito, a
é o análogo da
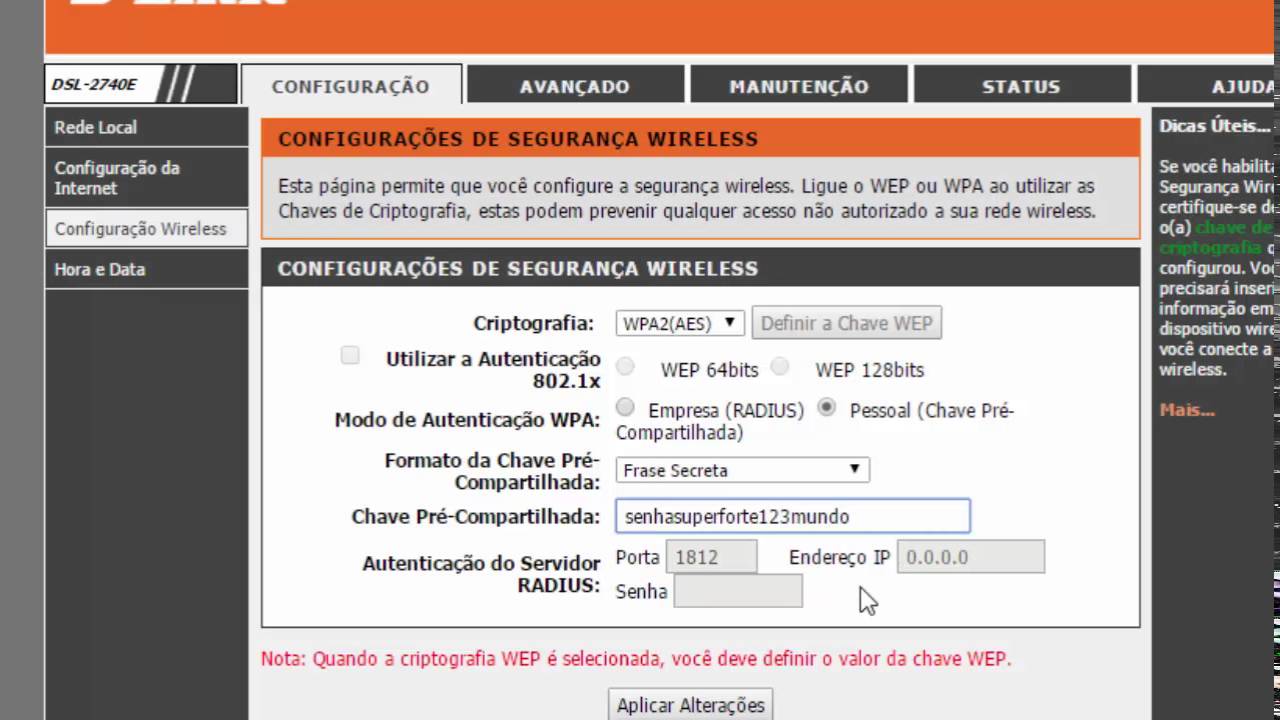
O AES cifra cada bloco iterativamente, em rodadas. Seja que depende de , há
Então, para nós, . Nestas rodadas, são geradas chaves, o texto claro substituído e transposto pelas seguintes operações:
Rodada :
AddRoundKey para adicionar (por XOR) a chave ao quadradoRodadas para cifrar, aplicando as seguintes funções:
SubBytes para substituir cada casa do quadrado (isto é, byte, sequencia de oito bites) por uma sequência de bites melhor distribuída,ShiftRows para transpôr as casas das linhas do quadrado,MixColumn para adicionar as casas das colunas do quadrado entre elas,AddRoundKey para gerar uma chave a partir da chave da rodada anterior e adicioná-la (por XOR) ao quadrado.Rodada para cifrar, aplicando as seguintes funções:
SubBytesShiftRowsAddRoundKeyIsto é, em comparação às rodadas anteriores, a função MixColumn é omitida: Revela-se que MixColumn e AddRoundKey, após uma leve modificação de AddRoundkey, podem trocar a ordem sem modificar o resultado final de ambas operações. Nesta equivalente ordem, a operação MixColumn não aumenta a segurança criptográfica, sendo a última operação invertível sem chave. Então, pode ser omitida.
O CrypTool 1 oferece no Menu Individual Procedures -> Visualization of Algorithms -> AES
Animation para ver a animação em Figura 3.1 das rodadas, eInspector em Figura 3.2 para experimentar com os valores do texto claro e da chave.
AES no CrypTool 1Vamos descrever estas funções em mais detalhes:
SubBytesSubBytes substitui cada baite do bloco por outro baite pela tabela de substituição S-box dada abaixo.
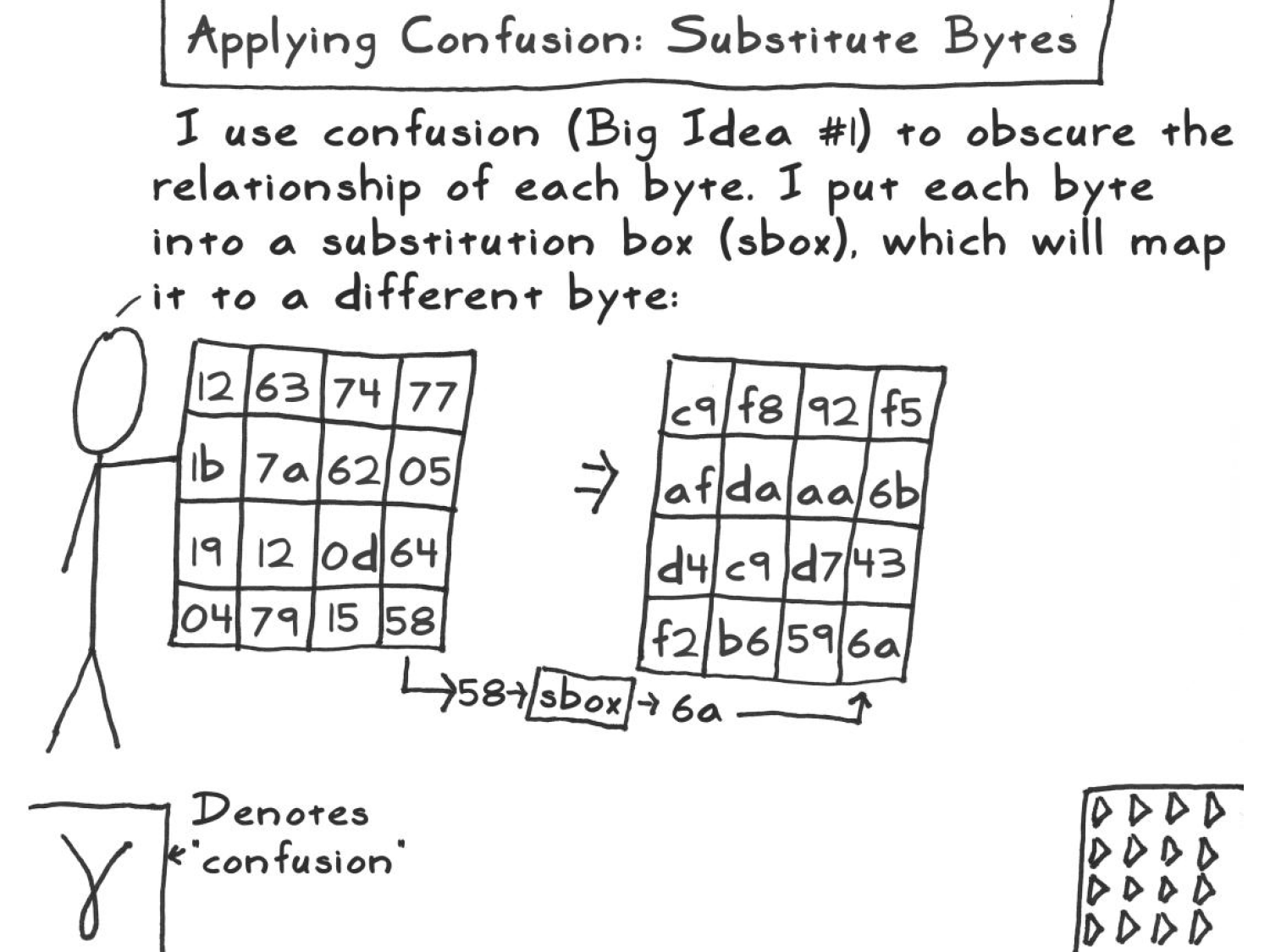
Para calcular o valor da casa pelo qual o S-box substitui o dado baite:
Calcula o seu inverso multiplicativo em ,
Calcula onde , , …, é o índice de cada bite de um baite, e
Em forma matricial, e como tabela calculada de antemão em notação hexadecimal (onde o número da linha corresponde ao primeiro e o número da coluna ao segundo digito do baite a ser substituído):
| 63 | 7c | 77 | 7b | f2 | 6b | 6f | c5 | 30 | 01 | 67 | 2b | fe | d7 | ab | 76 |
| ca | 82 | c9 | 7d | fa | 59 | 47 | f0 | ad | d4 | a2 | af | 9c | a4 | 72 | c0 |
| b7 | fd | 93 | 26 | 36 | 3f | f7 | cc | 34 | a5 | e5 | f1 | 71 | d8 | 31 | 15 |
| 04 | c7 | 23 | c3 | 18 | 96 | 05 | 9a | 07 | 12 | 80 | e2 | eb | 27 | b2 | 75 |
| 09 | 83 | 2c | 1a | 1b | 6e | 5a | a0 | 52 | 3b | d6 | b3 | 29 | e3 | 2f | 84 |
| 53 | d1 | 00 | ed | 20 | fc | b1 | 5b | 6a | cb | be | 39 | 4a | 4c | 58 | cf |
| d0 | ef | aa | fb | 43 | 4d | 33 | 85 | 45 | f9 | 02 | 7f | 50 | 3c | 9f | a8 |
| 51 | a3 | 40 | 8f | 92 | 9d | 38 | f5 | bc | b6 | da | 21 | 10 | ff | f3 | d2 |
| cd | 0c | 13 | ec | 5f | 97 | 44 | 17 | c4 | a7 | 7e | 3d | 64 | 5d | 19 | 73 |
| 60 | 81 | 4f | dc | 22 | 2a | 90 | 88 | 46 | ee | b8 | 14 | de | 5e | 0b | db |
| e0 | 32 | 3a | 0a | 49 | 06 | 24 | 5c | c2 | d3 | ac | 62 | 91 | 95 | e4 | 79 |
| e7 | c8 | 37 | 6d | 8d | d5 | 4e | a9 | 6c | 56 | f4 | ea | 65 | 7a | ae | 08 |
| ba | 78 | 25 | 2e | 1c | a6 | b4 | c6 | e8 | dd | 74 | 1f | 4b | bd | 8b | 8a |
| 70 | 3e | b5 | 66 | 48 | 03 | f6 | 0e | 61 | 35 | 57 | b9 | 86 | c1 | 1d | 9e |
| e1 | f8 | 98 | 11 | 69 | d9 | 8e | 94 | 9b | 1e | 87 | e9 | ce | 55 | 28 | df |
| 8c | a1 | 89 | 0d | bf | e6 | 42 | 68 | 41 | 99 | 2d | 0f | b0 | 54 | bb | 16 |
ShiftRowsShiftRows traslada a linha do quadrado posições para a esquerda (onde as linhas são enumeradas a partir de zero, isto é, percorre e e a traslação é cíclica). (Em particular, primeira linha não é trasladada.) Visualmente, o quadrado com entradas
é transformada em um com entradas
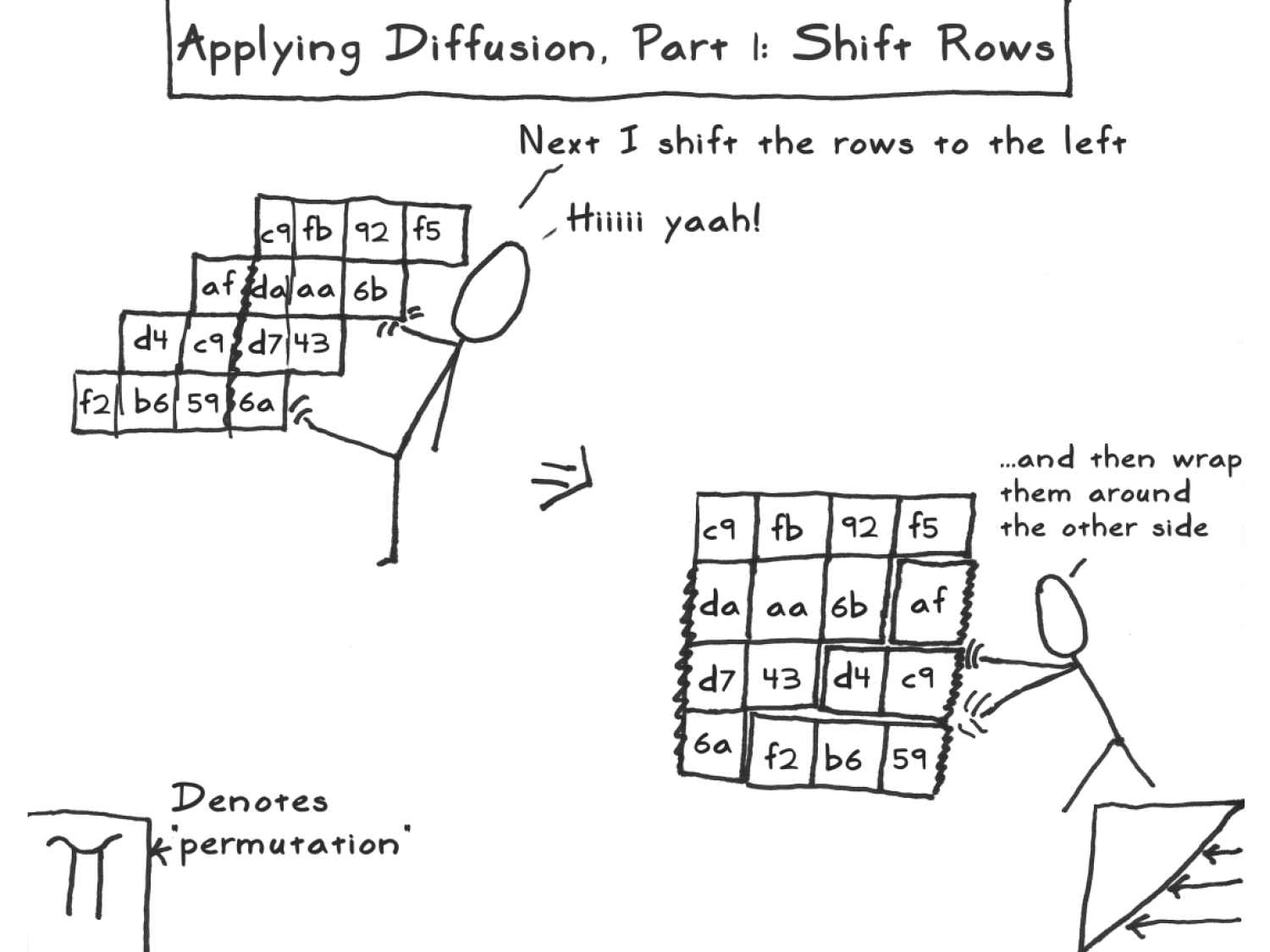
MixColumnMixColumn multiplica cada coluna do bloco por uma matriz fixa. Mais exatamente,
então Por exemplo, o baite é calculado por
AddRoundKeyAddRoundKey adiciona, pela operação XOR, a chave da rodada atual ao quadrado do texto cifrado, isto é, A chave é gerada coluna a coluna. Denotemo-las por , , e ; isto é, Como a chave tem baites, cada coluna tem .
A primeira chave , isto é, da primeira rodada, é dada pela chave inicial .
Para (onde é o número total de rodadas, para nós), as quatro colunas , , e da nova chave são geradas a partir das colunas da antiga chave como segue:
ScheduleCore aplicada à primeira coluna da chave da rodada precedente (que denotemos por ); aqui ScheduleChore é a composição das transformações:
SubWord: Substitui cada um dos baites de segundo a S-box em SubBytes.RotWord: Traslada um baite à esquerda.Rcon(): Adiciona (por XOR) a o valor constante, em notação hexadecimal, [] onde a potencia (= produto iterado) é calculada no corpo de Rijndael . Isto é, o único baite que muda é o primeiro, pela adição, ou do o valor (para ), ou do valor em para .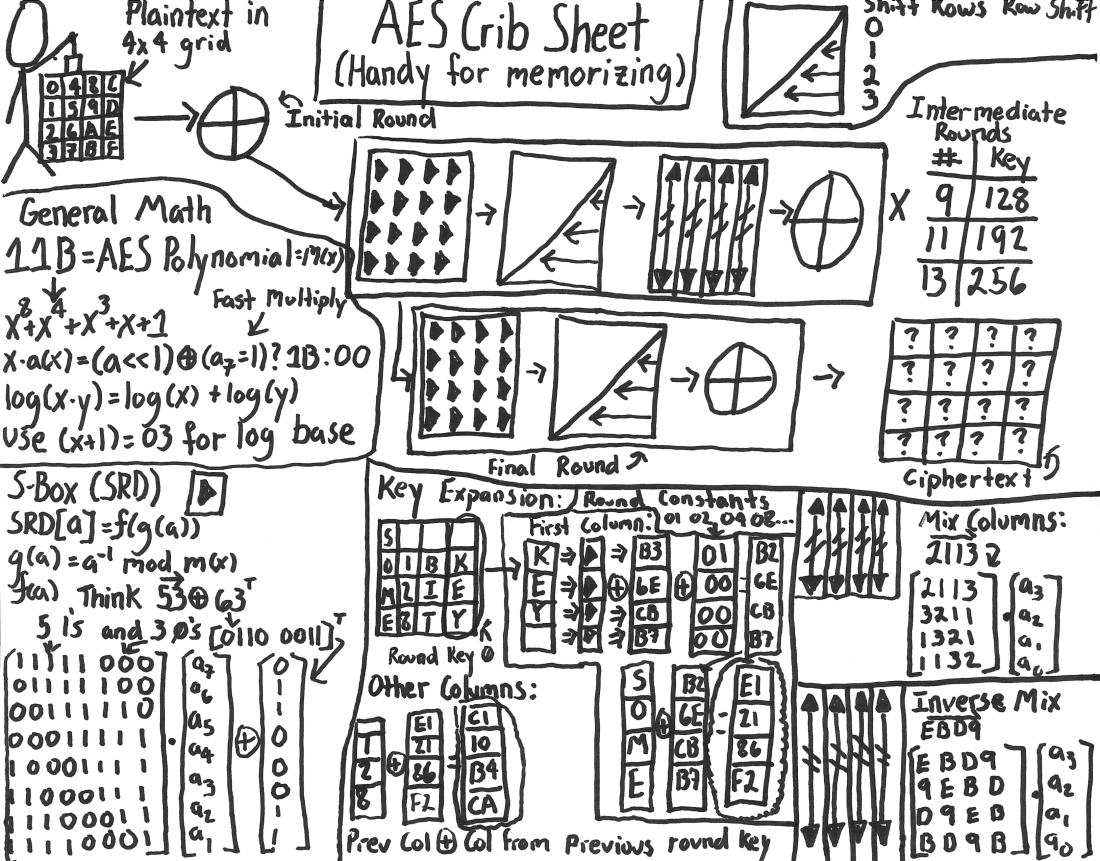
Observamos que a única transformação que não é afim (isto é, dada por um polinômio de grau , ou, equivalentemente, a composição de uma aplicação linear e um traslação) é a inversão no corpo na operação SubBytes. Com efeito
SubBytes são aplicadas, nesta ordem,
ShiftRows é uma permutação, em particular,linear.MixColumn é uma adição, em particular, linear.AddRoundKey é a traslação pela chave da rodada.Quanto às metas da difusão e confusão, podemos ressaltar que a cada etapa são substituídos e transpostos cerca da metade dos bites (no SubBytes) ou baites (no MixColumn e ShiftRows). Para convencer-se da complementaridade das simples operações para segurança criptográfica, isto é, que geram em conjunção alta confusão e difusão após de poucas iterações,
vale a pena experimentar em Individual Procedures -> Visualization of Algorithms -> AES -> Inspector com uns valores patológicos, por exemplo:
00, e00 e do texto claro iguais a 00 exceto uma entrada sendo igual a 01, isto é, mudar um singelo bite.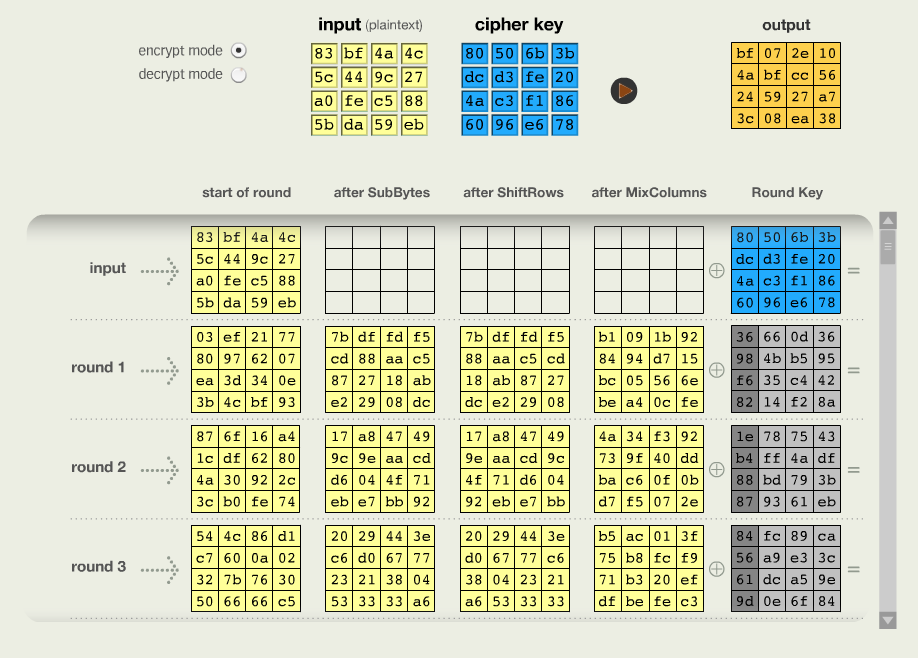
AES no CrypTool 1Vemos como se espalha esta pequena diferença inicial, gerando já resultados totalmente diferente após, digamos, quatro rodadas! Isto torna plausível a imunidade do AES contra a criptoanálise diferencial como será mostrado em Seção 3.6.
No caso que todas as entradas da chave e do texto claro sejam iguais a 00, compreendemos também o impacto da adição da constante Rcon à chave em cada rodada: é dela que provém toda a confusão!
AES contra a Criptoanálise DiferencialO principio principal é o de Shannon, da boa difusão e confusão. Idealmente, cada bite cifrado depende de cada bite da chave e do texto claro; se um bite da chave ou do texto claro muda, então todo bite do texto cifrado muda com uma probabilidade de .
Contra a criptoanálise diferencial, isto é, para evitar trilhas diferenciais altamente prováveis, o AES usa
S-box cuja tabela de distribuição diferencial tem como entrada máxima (sendo o mínimo), masO quociente de propagação para um diferencial , uma diferença entrante e diferença sainte para uma aplicação é
O peso de restrição de um diferencial é
Se a aplicação é afim (isto é, , um polinômio de grau , ou, equivalentemente, a composição de uma aplicação linear e um traslação ), o quociente de propagação é para e senão.
Se , então para e tem quociente de propagação e peso de restrição
Uma trilha diferencial é uma sequência finita de diferenças tal que o resultado do diferencial seja a entrada do diferencial seguinte .
O peso de restrição de uma trilha diferencial é
É inviável calcular o quociente de propagação de uma trilha diferencial, mas fácil calcular o seu peso de restrição. Se os diferenciais da trilha diferencial são pouco correlacionados, então Esta aproximação, por exemplo, para DES, é muito boa se . Se , então não pode valer mais. Neste caso, em média apenas uma fração das trilhas diferenciais com peso com uma diferença inicial ocorrem.
Observamos que o peso de restrição de uma trilha independe das chaves das rodadas, porque cada peso de restrição é. Contudo, o quociente de propagação da trilha depende das chaves. Porém, pela aproximação , uma trilha diferencial com peso de restrição significantemente tem um quociente de propagação que pode ser considerado independente das chaves das rodadas.
O passo da permutação é subdividido em dois sub-passos
ShiftRows, que opera sobre cada linha do blocoMixColumn, que opera sobre cada coluna do blocoe os quais, em combinação, conseguem uma excelente confusão e difusão porque garantem trilhas largas, diferenciais com muitos baites ativos, após poucas rodadas. Mais exatamente, Teorema 2 mostrará que após quatro rodadas, qualquer trilha diferencial tem baites ativos, isto é, o dos baites diferentes de em todos os diferenciais na trilha diferenciais é .
Daqui por diante, um vetor é uma sequência finita. Um vetor de bites (por exemplo, um bite, um baite, um vetor de baites) é ativo se é diferente de . Para um vetor de baites , seja o peso de . Recordemo-nos de que uma aplicação entre vetores de baites é linear se .
Definição. Para uma aplicação linear entre espaços de vetores de baites, seja o seu número de ramificação.
Isto é, para ser grande, quanto menos baites diferentes de em , tanto mais em . Como F = MixColumn opera sobre vetores de baites, . Com efeito, vale igualdade:
Lema 1. O número de ramificação da aplicação linear MixColumn é .
Em particular, para qualquer vetor que tem um único baite diferente de , a sua imagem tem quatro baites diferentes de .
Para , , …,
ShiftRows na rodada .Em particular, é aplicado MixColumn para obter .
Uma trilha (diferencial) é uma sequência finita de diferenciais (de pares de baites); em particular, é uma sequência finita, ou vetor, de baites e podemos contar o seu peso, isto é, contar ao início de cada rodada o número de baites diferentes de e somá-los. Isto é, o peso de uma trilha é .
Como SubBytes opera baite a baite, e AddRoundKey não muda o diferencial, observamos que as únicas operações que mudam os baites ativos em uma trilha diferencial são ShiftRows e MixColumn. Além disso,
MixColumn, eShiftRows.Em particular, e .
Teorema 1. Para uma trilha diferencial sobre duas rodadas, onde é o número de baites ativos da trilha e é o número de colunas ativas na entrada da segunda rodada.
Demonstração: Como pelo Lema 1 o número de ramificação de MixColumn é , em cada coluna, a soma do número de baites ativos em e é . Logo,

Em particular, toda trilha sobre duas rodadas tem baites ativos.
Lema 2. Em uma trilha diferencial sobre duas rodadas, onde e são os números de colunas ativas na entrada e saída da trilha.
Demonstração: Como ShiftRows move cada baite diferente a uma coluna diferente, observamos e quer dizer, antes e depois de ShiftRows.
Seja uma coluna (isto é, os baites do bloco nas posições dadas por esta coluna, independente da rodada) que é ativa em , na entrada da segunda rodada (ou, equivalentemente, em , após ShiftRows na primeira rodada). Temos e, da mesma maneira, Como MixColumn tem número de ramificação , e pois segue

Teorema 2. Toda trilha diferencial sobre quatro rodadas tem baites ativos.
Demonstração: Tem-se onde
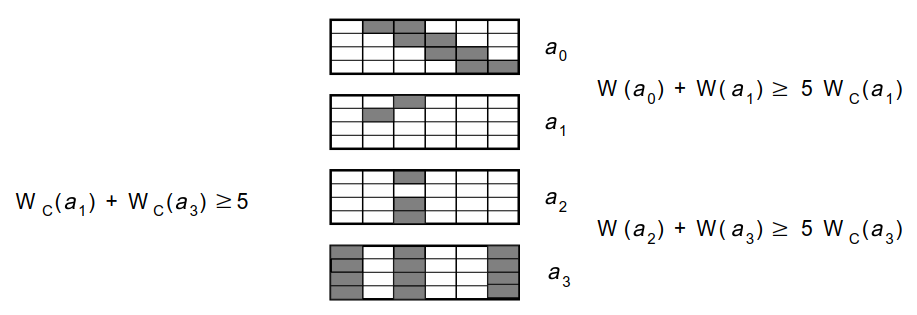
Corolário: Não há trilhas com uma probabilidade maior que para rodadas de AES.
Demonstração: Como a S-box tem um quociente de propagação de e uma trilha com rodadas pelo menos S-boxes ativas. Por Capítulo 5 em Daemen (1995), a probabilidade da trilha é aproximadamente o produto da probabilidade de cada S-box.
A criptografia assimétrica foi sugerida pela primeira vez, publicamente, em Diffie e Hellman (1976).

Por trás dela figura uma função alçapão (mais especificamente, nesse artigo, a exponencial modular), uma função invertível que é facilmente computável, mas cujo inverso é dificilimamente computável em ausência de uma informação adicional, a chave secreta.
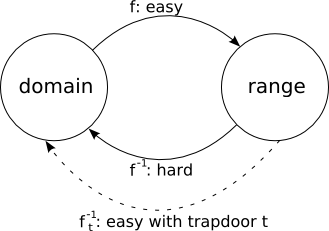
Para cifrar, aplica-se a função, para decifrar, seu inverso com a chave secreta. Por exemplo, na abordagem segundo Diffie e Hellman, esta função é a exponencial, porém, sobre outro domínio que os números reais a que estamos acostumados, explicado em Seção 5.1.
Com efeito, Diffie e Hellman (1976) introduziu apenas um esquema para trocar uma chave secreta através de um canal inseguro. Foi foi realizado pela primeira vez
RSA foi criado, eElGamal, mais recente, mas é o exemplo mais próximo do esquema original.
RSA, Rivest, Shamir e AdlemanRecordemo-nos de que há duas chaves, uma chave pública e outra privada, Comumente:
Assim, um texto pode ser transferido do cifrador (Alice) a uma pessoa só, o decifrador (Bob).
Os papéis das chaves públicas e privada podem ser invertidos:
Assim, o cifrador pode provar a todos os decifradores (os que têm a chave pública) a sua posse da chave privada; a assinatura digital.
A teoria (quer dizer a matemática) por trás da cifração pela chave pública (mensagens digitais) ou privada (assinatura digital) é quase a mesma; unicamente os papéis dos argumentos da função alçapão são invertidos. (Por exemplo, no algoritmo RSA, esta troca de variáveis é verdadeiramente tudo o que acontece.) Porém, na prática, geralmente são cifrados:
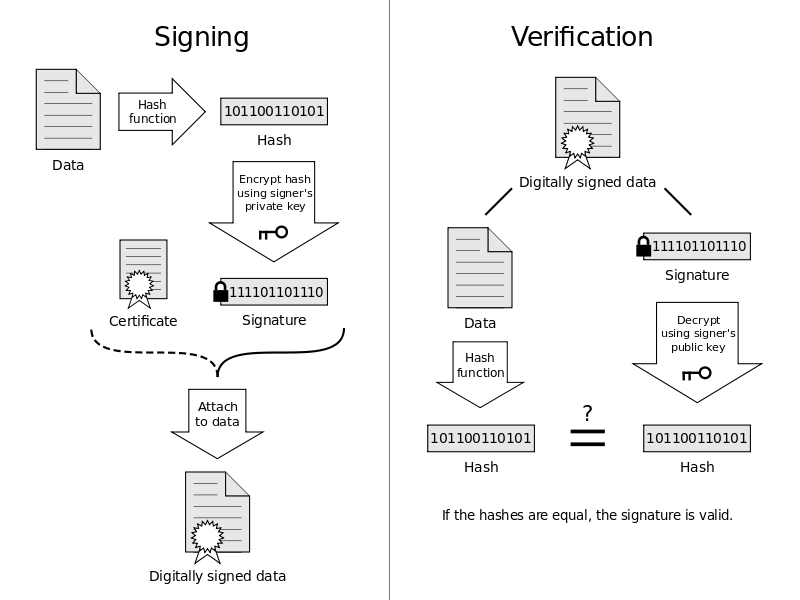
Isto é, enquanto
Uma subchave de uma chave principal é uma chave (cuja soma de verificação criptográfica é) assinada pela chave principal.
O dono frequentemente cria subchaves a fim de usar a chave (pública e privada) principal unicamente
e as subchaves para os outros fins quotidianos (assinar e decifrar) com um maior risco de comprometimento.
Desta maneira o eventual comprometimento de uma subchave (o que é mais provável pelo seu uso quotidiano!) não comprometerá a chave principal. Neste caso,
Estudamos como as subchaves funcionam em prática no aplicativo criptográfico principal, o programa de linha-de-comando GPG discutido em Seção 4.6. Uma boa referência é https://wiki.debian.org/Subkeys.
Para mais segurança, o usuário cria (por exemplo, em GPG)

GPG para Subscrever e EncriptarQuanto ao uso de chaves diferentes para assinar e cifrar,
ElGamal,RSA.pois
pois, por exemplo no algoritmo RSA, a assinatura e a decifração (pela chave privada) são matematicamente iguais!
Por isso, a assinatura (pela chave privada) de um documento cifrado pela chave pública equivale à decifração! Porém, esta possibilidade é teórica, mas não pratica: Todas as implementações do RSA protegem o usuário pelo fato que sempre e exclusivamente
Unicamente a chave principal é imutavelmente ligada a identidade do dono, e todas as outras substituíveis: Enquanto a
Pelo programa paperkey que extrai a parte secreta (do arquivo) da chave privada (isto é, omite todas as informações publicas como
e codifica esta parte em notação hexadecimal (armazenado em um arquivo de texto). (Por isso, se a chave tem, por exemplo, bites, o arquivo gerado por paperkey tem baites.) Este comando
gpg --export-secret-key 0xAE46173C6C25A1A1! > ~/private.sec
paperkey --secret-key ~/private.sec > ~/private.paperkey!) a chave secreta principal (0xAE46173C6C25A1A1) das chaves privadas, epaperkey em um arquivo de texto.Pelo programa qrencoder (para chaves cujo arquivo tem caracteres) que a codifica em um código QR.
a leitura das chaves de um cartão inteligente é muito mais difícil do que de um arquivo (armazenado num pendrive ou HD)
deixa menos traços:
keyloggers que gravam as letras tecladas.
Na (Perfect) Forward Secrecy (sigilo futuro perfeito), depois que os correspondentes trocaram as suas chaves públicas (permanentes) e estabeleceram confiança mútua,
MITM (vide Seção 4.2).,Desta maneira, mesmo se a correspondência foi espreitada e gravada, não pode ser decifrada posteriormente; em particular, não pode ser decifrada pela obtenção da chave privada de um correspondente.
Por exemplo, o protocolo TLS que cifra a comunicação em grande parte da internet, tem em versão 1.2 suporte para Perfect Forward Secrecy:
TLS.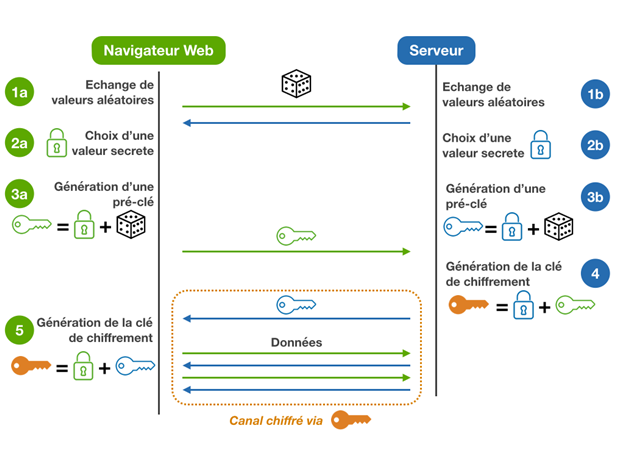
Deve ser pensado com solenidade antes de assinar qualquer documento. O mesmo vale para assinaturas digitais.
Uma assinatura tem como vantagem a garantia que o dono da chave privada escrevesse o conteúdo. Na comunicação por e-mails, evita o risco que um atacante
Porém, como inconveniência, caro leitor, se a comunicação contém algo que não desejas ser visto por terceiros (por exemplo, ser lido em voz alta pelo promotor público no tribunal), melhor não comproves a tua origem pela tua assinatura! Como esta mensagem pode ser espreitada, o teu correspondente mudar de ideia sobre a tua privacidade ou a sua conta ser hackeada, …
Para dar uma analogia à realidade nossa, uma assinatura automática compara-se a gravação de toda conversa privada; esperemos que ninguém tenha acesso a ela!
Observamos que Alice quer provar ao Bob que ela é a remetente, mas não a terceiros! Por isso surgiu a ideia da assinatura de grupo: uma chave efêmera para assinar é criada e compartilhada (isto é, a chave pública e privada) entre Alice e Bob. Desta maneira, Alice e Bob têm certeza sobre o originário, mas terceiros apenas que ele pertença ao grupo.
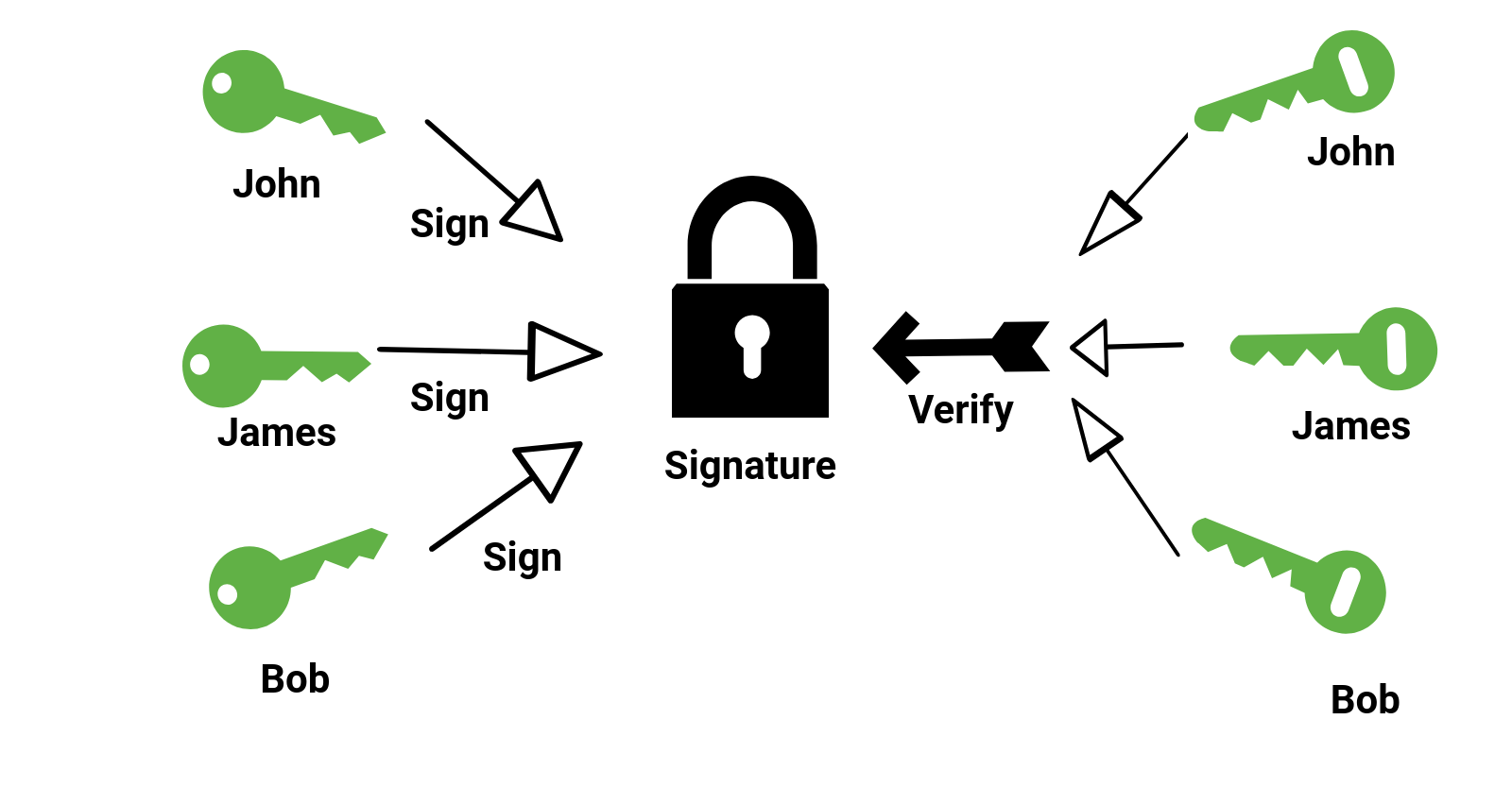
MITMA criptografia assimétrica permite a Alice, que conhece uma chave pública,
Com este conforte que a criptografia assimétrica (em contraste com a criptografia simétrica) permite à Alice, obter a chave pública impessoalmente sem encontrar o Bob, surge o problema da identidade do dono da chave pública: Considerando que a Alice
como garantir à Alice a identidade da chave privada, isto é, que o dono da chave privada seja verdadeiramente o Bob?
Quer dizer, como evitar um ataque “man-in-the middle” — MIM (talvez “Maria-Bonita-no-Meio” em português nordestino) ? No MIM, o atacante se interpõe entre os correspondentes, assumindo a identidade de cada um, assim observando e interceptando suas mensagens:
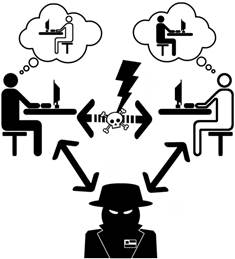
Suponhamos que Maria Bonita intercepte a correspondência entre Alice e Bob.
Assim, Alice como Bob são persuadidos que usem a chave pública do outro, mas, na verdade, é a da Maria Bonita!
Em termos práticos, este problema ocorre por exemplo no protocolo ARP, o Protocolo de Resolução de Endereços (do inglês Address Resolution Protocol) de 1982 (na RFC 826) que padroniza a resolução de endereços (conversão) da camada de internet em endereços da camada de enlace. Isto é, o ARP mapeia um endereço de rede (por exemplo, um endereço IPv4) em um endereço físico como um endereço Ethernet (ou endereço MAC). (Em redes Internet Protocol Version 6 (IPv6), o ARP foi substituído pelo NDP, o Protocolo de Descoberta de Vizinhos (do inglês Neighbor Discovery Protocol).)
O ataque de ARP poisoning (= poluição de cache ARP) procede como segue:
Maria Bonita quer interceptar as mensagens da Alice ao Bob, todos os três fazendo parte na mesma rede física.
arp who-has à Alice que contem como endereço de IP fonte o do Bob cuja identidade queremos usurpar (ARP spoofing) e o endereço físico MAC da placa de rede de Maria Bonita.MAC de Maria Bonita ao endereço IP do Bob.IP, será Maria Bonita que receberá os pacotes da Alice!Esta garantia da integridade da identidade é estabelecida por terceiros, isto é, identidades com chaves privadas que confirmam pelas suas assinaturas digitais que o Bob é o dono da chave privada.
O problema da identidade das chaves públicas surge outra vez: Como garantir que as identidades dos donos das chaves privadas sejam verdadeiras?
Há duas soluções:
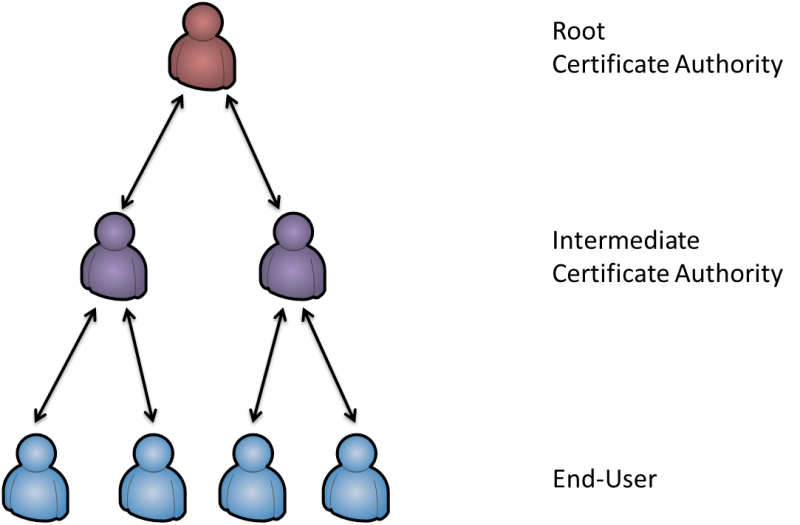
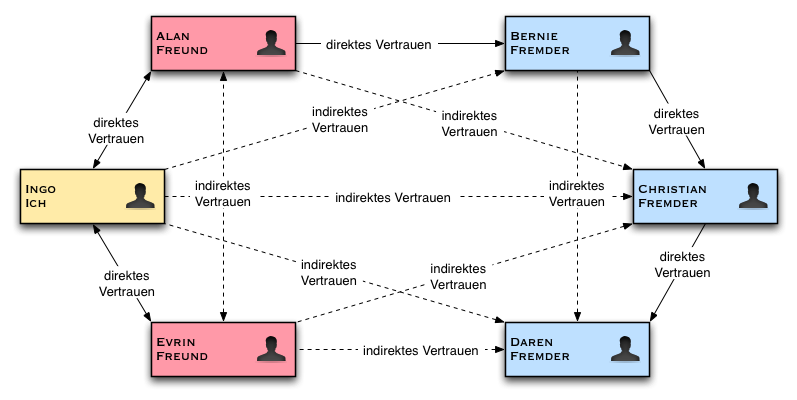
Nas autoridades hierárquicas, os donos de chaves privadas distinguem-se por níveis hierárquicos. No nível o mais alto jazem as autoridades radicais nas quais se confia incondicionalmente. Por exemplo,
VeriSign, GeoTrust, Comodo, … são grandes empresas certificadoras estado-unidenses;Let's encrypt sem fins lucrativos;/etc/ssl/certs na distribuição de Linux openSUSE revela que existe
T-TeleSec da Deutsche Telekom AG, a antiga operadora de telecomunicação nacional),Staat der Nederlanden),Firmaprofesional, ACCVRAIZ1 — Agencia de Tecnología y Certificación Electrónica, e ACC RAIZ FNMT — Fábrica Nacional de Moneda y Timbre),Firefox jazem na base-de-dados cert8.db na pasta do perfil do usuário [por exemplo, %APPDATA%/Mozilla/Firefox/<perfil>/cert8.db em Microsoft Windows > 7], mas precisa compila o programa certutil para lê-lo.)ICP, Instituto Nacional de Tecnologia da Informação da Casa Civil da Presidência da República, cuida da infraestrutura de chaves públicas. Em particular, credencia as autoridades radicais: Na lista destas autoridades, figuram, entre outras,
SERPRO - Serviço Federal de Processamento de Dados, primeira Autoridade Certificadora credenciada pela ICP-BrasilCaixa Econômica Federal, a única instituição financeira credenciada como Autoridade Certificadora da ICP-BrasilAC Digitalsign, uma empresa portuguesaPKD da Organização da Aviação Civil Internacional — ICAO, agência especializada das Nações Unidas.SERASA Experian, que fornece certificados digitais para quase todos os grupos financeiros participantes do Sistema de Pagamentos Brasileiro — SPB./etc/ssl/certs, ouChrome ou Firefox.Na teia de confiança, os donos de chaves privadas não se distinguem de um ao outro.
A ausência de autoridades radicais, entidades incondicionalmente confiáveis, é compensada pela
SMS, mensageiro instantâneo, …) eNa internet,
X.509, com o seu maior uso de cifrar a comunicação entre o usuário e um site (frequentemente comercial), eOpenPGP (e principalmente implementado pelo programa GnuPG), com o seu maior usa de cifrar os e-mails entre dois usuários. Este esquema radicalmente rejeita qualquer hierarquia: o usuário pode publicar uma chave pública com um endereço de e-mail em um servidor de chaves públicas (por exemplo, em pgp.mit.edu) sem sequer confirmar (por um e-mail de ativação) que tem acesso à conta deste endereço de e-mail.Comparamos as vantagens e inconveniências entre as duas abordagens:
X.509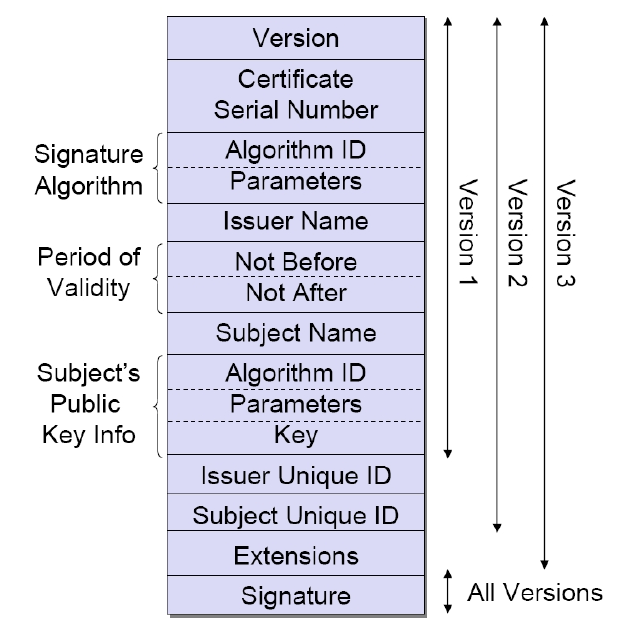
X.509A assinatura de um certificado X.509 é a cifração pela chave privada do hash da concatenação de
V = versão X.509,SN = número de série do certificado,AI = número identificador do algoritmo,CA = nome da autoridade certificadora,TA = tempo de intervalo de validade do certificado,A = nome do sujeito, eKA = chave pública do sujeito.O sistema de autoridades hierárquicas foi criado para estabelecer a confiança através de máquinas e tem como grande vantagem
Porém, confiança é uma questão humana, e tem como calcanhar-de-aquiles a confiança (absoluta) na autoridade (radical):
a confiança absoluta que a chave pública pertença à autoridade;
a confiança absoluta que a chave privada da autoridade não seja comprometida;
a confiança que a autoridade não abuse do seu poder. Por exemplo, cobrar indevidamente caro; (Esta observação levou a recente criação da autoridade livre Let’s Encrypt que
VeriSign cobra por cada certificado 399$ por um ano),a confiança que a autoridade trabalhe seriamente, por exemplo, na verificação da identidade do terceiro pela autoridade. A este fim, cada certificadora radical é sujeita a pareceres de auditorias periódicos (que leva a questão recursiva se o mesmo vale para quem faz as auditorias?!). Além disto, o nível de segurança reflete-se pela forma do cadeado na barra-de-endereço do navegador:
domain certificate, a verificação é completamente automatizada; nenhuma verificação fora de linha é feita. Basta ter acesso ao domínio para obter o certificado.extended certificate a verificação do proprietário do site é feita pessoalmente.Por isso, para ter certeza que o site pertença a quem pretende (por exemplo, evitar a confusão entre bancobrasil.com.br e bancobrazil.com.br), é importante verificar na barra-de-endereço que o cadeado indique um extended certificate; por exemplo, os navegadores Firefox e Chrome indicam-no pela cor verde do nome da entidade.
Pelo cadeado comum que corresponde a um domain certificate, o usuário apenas tem certeza que comunique com o dono do domínio, mas não que ele pertence à empresa ou organização que o site aparenta representar. Quer dizer, o cadeado (ou certificado) comum,
Isto é, mesmo se o cadeado do certificado comum desperta confiança, a sua emissão automatizada
MITM por DNS Cache poisoning, em que o endereço do nome (por exemplo, bancobrasil.com.br) é resolvido ao endereço numérico IP de outro servidor, contudoMITM pela confusão do usuário entre o endereço e a pessoa (jurídica).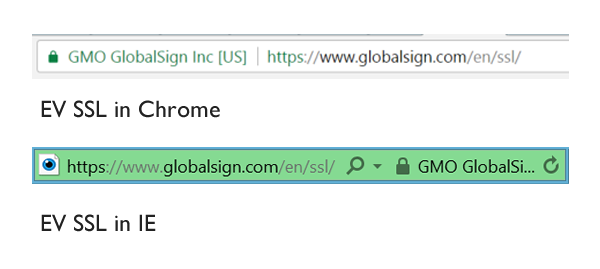

o respeito à autoridade, isto é, o receptor do certificado tem de saber se pode confiar na chave pública da autoridade ou não.
Por exemplo, nem o Chrome, nem o Firefox confiam na autoridade radical brasileira principal SERPRO; isto é, não inclui o seu certificado (= chave pública e auto-assinatura). Para o usuário, como o certificado auto-assinado
SERPROé desconhecido, aparece o seguinte alerta:
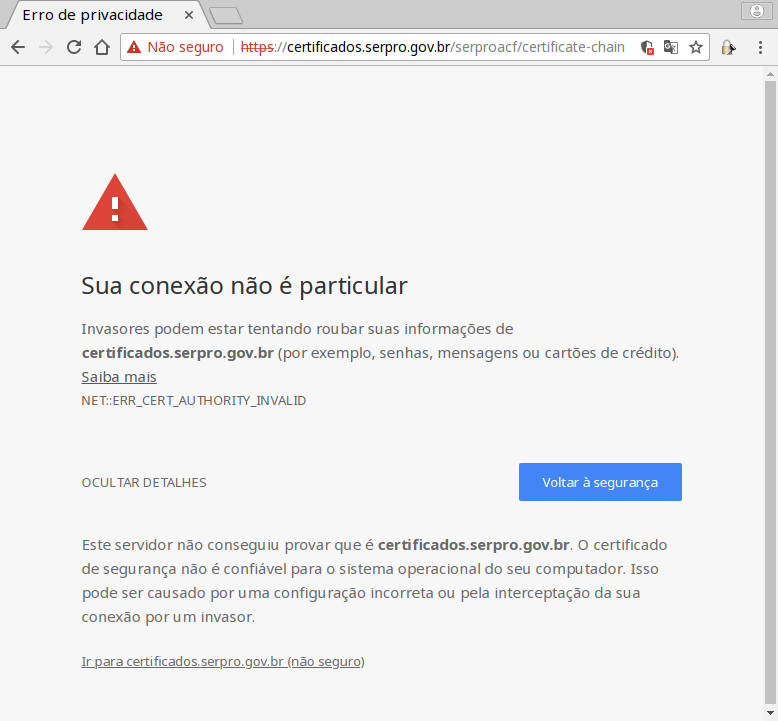
SERPROPor isso, por exemplo,
Caixa Económica Federal,
SERPRO),COMODO RSA,DETRAN em Alagoas,
SERPRO),Let's Encrypt.X.509Relatamos o maior uso do padrão X.509 na internet, o TLS Handshake:
Transport Layer Security, Segurança da Camada de Transporte (antigamente Secure Sockets Layer — SSL, Protocolo de Camada Segura de Soquetes), o protocolo que cifraTransmission Control Protocol — TCP.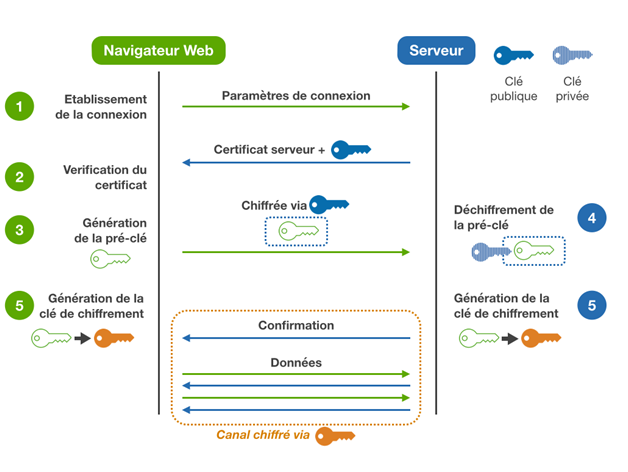
A referência definitiva é a especificação RFC 5246. Uma ótima visão global é dada pela Conexão Ilustrada de TLS 1.3 com cada baite explicado.
São os primeiros passos entre um cliente e o servidor, por exemplo, um site de comércio eletrônico, para estabelecer uma conexão cifrada (por exemplo, para receber os dados do cartão de crédito do cliente).
Opcionalmente,
RSA,ECC ou ElGamal).O “Alô” entre o cliente e o servidor, em que o cliente propõe, e o servidor escolhe, um pacote criptográfico; isto é, o conjunto dos algoritmos criptográficos,
MD5, SHA, …), eRSA, …),RSA, ECC, …),AES, Camellia, RS4, …). Frequentemente, é escolhido não o algoritmo simétrico mais seguro, mas, sim, o algoritmo mais econômico pelo servidor.Por exemplo, o pacote criptográfico TLS_RSA_WITH_3DES_EDE_CBC_SHA (codificado 0x00 0x0a) usa
RSA para autentificar e trocar as chaves,3DES em modo CBC para cifrar a conexão, eSHA como hash criptográfico.Além disto, cada um,
criam um nonce, isto é, um número de uso único, que contém
que evita um ataque de repetição (replay attack); isto é, a reutilização das autentificações em outras sessões.
O servidor identifica e autentifica-se pelo
X.509:
X.509Este contém (principalmente):
VeriSign), e a sua assinatura digital (usando o hash criptográfico e o algoritmo assimétrico já combinados); isto é, a cifração pela chave privada da autoridade (de uma soma de verificação criptográfica)
Na imagem, temos o servidor www.detran.al.gov
Let's Encrypt Authority X3DST Root CA X3O cliente procura a chave pública da autoridade (radical) indicada no certificado (que é usualmente inclusa no navegador), e usa-a para decifrar esta assinatura digital. Se o resultado é a soma de verificação esperada (isto é, do endereço do servidor e da sua chave pública), então
Como o cliente (ou, mais exatamente, o seu navegador) confia incondicionalmente nas autoridades radicais, a este ponto ele tem certeza que a chave pública pertença verdadeiramente ao servidor visado.
(Opcionalmente, neste ponto também o cliente se autentifica por um certificado.)
O cliente
pré-master-secret), um número (pseudo-)aleatório de baites,O servidor
O cliente e o servidor calculam o segredo (master secret), um número de baites, por uma função PRF, master_secret = PRF(pre_master_secret, ClientHello.random + ServerHello.random) que usa como variáveis
nonces, comunicados no Alô,
O cliente e o servidor calculam quatro chaves simétricas (para o algoritmo combinado inicialmente, por exemplo, se é AES, cada uma de baites) a partir do segredo; nomeadamente:
client_write_MAC_secret,server_write_MAC_secret,client_write_key, eserver_write_key.Entre elas,
Que cada lado tem uma chave diferente se deve à melhor prática (best practice) de usar uma chave diferente para cada uso diferente.
OpenPGPVamos discutir:
OpenPGP:O sistema da teia de confiança modela o estabelecimento da confiança humana e tem como grande vantagem que
e como grande inconveniência que
Além disso,
expõe informação como
não escala bem; isto é, a quantidade de armazenagem para a teia de confiança do mundo inteiro seria imensa. Para o nível de autentificação que fornece, não faz sentido nestas escalas; infelizmente, confiamos com convicção na chave da outra pessoa quando confiamos em todos os terceiros que testemunham a sua autenticidade, isto é, quando conhecemo-los pessoalmente.
quão séria é a confiança testemunhada pelos terceiros na teia? Por exemplo, as ditas key-sign parties comumente juntam desconhecidos que assinam as suas chaves um ao outro. Isto é o contrário de que confiança significa: Só deve ser passada quando conhecemos bem o dono da chave que assinamos!
A teia é tão segura quanto a sua malha menos segura; isto é, uma malha da teia (facilmente) comprometida põe todos os seus fios em risco: Uma chave comprometida pode ser usada para assinar qualquer outra chave na teia de confiança.
Por exemplo, imagina que Alice quer cifrar uma mensagem a Bob. Seja a chave de Carlos comprometida pelo man-in-the-middle.
man-in-the-middle
Mesmo se esta fraude for descoberta por outros (a ideia da teia de confiança é que é impossível enganar todo mundo), certo estrago já foi feito.
Na prática, em vez da teia de confiança, é mais viável estabelecer a confiança por outro canal impessoal (pela troca das impressões digitais das chaves públicas), por exemplo,
SMS,Telegram ou WhatsApp,OpenPGPApesar da absurdidade (visto que confiança é uma questão humana e pessoal) da confiança automática do usuário prestada às certificadoras radicais (sobretudo empresas),
X.509 é, pelo seu conforto para o usuário, ubíquo no comércio eletrônico,OpenPGP para comunicar por e-mail.Avaliam principalmente o esforço para a instalação do programa e a manutenção das chaves (a qual inerentemente necessita da estimativa do usuário para a confiança nas chaves usadas) desproporcionalmente grande para o benefício (da maior privacidade e segurança) obtido. Infelizmente, justamente porque tão poucas pessoas usam OpenPGP, a usabilidade dos programas dedicados melhorou pouco nos últimos anos.
Por isso:
OpenPGP e que serão apresentados em Seção 4.6. Mesmo se usuário perde (em parte) o controle sobre a confiança, a ganha de conforto ajuda a divulgar este protocolo para leigos. O tipo de segurança que oferecem chama-se Opportunistic Security: enquanto ninguém se interesse, é seguro; caso contrário, é vulnerável ao ataque pelo man-in-the-middle.OpenPGP tem as suas insuficiências concepcionais:
PFS); mesmo se o usuário típico quer guardar os e-mail escritos e lidos e prefere chifrá-los no seu computador pela mesma chave, é mais seguro cifrar o e-mail para o transporte (através do servidor do remetente e destinatário) por uma chave efêmera. (Consta-se, porém, que muitos usuários guardam localmente copias em texto claro das suas mensagens, o que compromete o esforço criptográfico no transporte.)OpenPGP usa o protocolo de e-mail que não cifra o conteúdo, omite-se facilmente a cifração por mal uso do cliente de e-mail. (Pode ser pensado em usar um cliente de e-mail exclusivamente dedicado a comunicação cifrada.)Recentemente, surgiu o programa opmsg (como alternativa a GPG que será apresentado em Seção 4.6) que implementa (muitos métodos d’) o protocolo Off the Record — OTR (como alternativa a OpenPGP) que oferece:
Perfect Forward Secrecy: o comprometimento das chaves privadas não compromete as conversas cifradas anteriores (porque uma chave efêmera é criada para o envio de cada mensagem e apagada após o recebimento)ring signature, que compartilha a chave secreta para assinar entre todos os correspondentes; por este recurso surge a necessidade de usar uma chave para cada correspondente!)Além disso
opmsg) para cada correspondente,OpenPGPApresentamos uns programas que usam a teia de confiança (o protocolo OpenPGP), como
GPG para criar chaves e (de)cifrar e assinar/autenticar por elas,Enigmail para o cliente de e-mail livre Thunderbird, que recentemente automatiza este processo pelo suporte a AutoCrypt,Mailvelope para cifrar os e-mails nos sites como gmail.com e Hotmail.com, entre outros, eDelta-Chat para Android que tem pelo uso do protocolo de e-mail a vantagem de não depender de um servidor só da empresa fornecedora, como o WhatsApp.GPGO programa GnuPG é um programa de linha-de-comando e pouco acolhedor para principiantes. Serve para a funcionalidade criptográfica de muitos programas criptográficos com interface gráfica.
GPGOferecer ao grande público aberta e gratuitamente métodos criptográficos para cifrar dados eletrônicos confidenciais.
Um programa de linha-de-comando para
Linux, eMac OS e Microsoft WindowsGnu Privacy Guard (= GPG) pelo alemão Werner Koch começou (e até hoje não cessou) para ter uma alternativa livre ao programa de criptografia de e-mail comercial Pretty Good Privacy (= PGP) por Phil Zimmermann. Até hoje, é o desenvolvedor principal e depende de doações como única fonte de renda. No ínico de 2015, os seus recuros estavam acabando e pediu ajuda financeira, a qual recebeu amplamente.
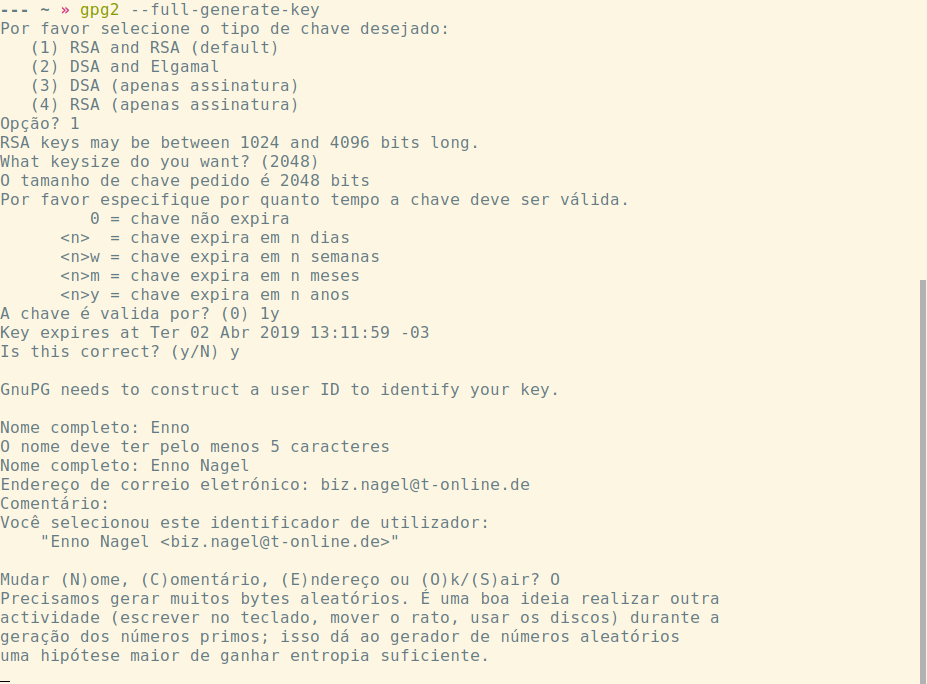
GPG na linha-de-comandoCria um par de chaves, uma pública e a outra privada, escolhendo
RSA),A chave pública é destinada à divulgação. Ela serve
A chave privada é guardada e protegida por uma senha. Ela serve
EnigmailO programa Enigmail é uma extensão para o programa de e-mail gráfico Thunderbird que adiciona a este a função de
pelo GnuPG, assim que o usuário pode aceder a estas funções por botões no próprio Thunderbird.
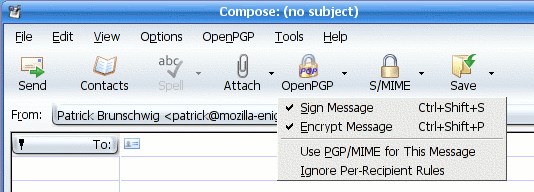
MailvelopeO Mailvelope é uma extensão para os navegadores Firefox e Chrome, desenvolvido por uma empresa alemã, que adiciona recursos de criptografia e descriptografia à interface de provedores comuns de webmail como:
GmailHotmail.comYahoo!Por exemplo, cifra e decifra mensagens (usando o padrão OpenPGP), arquivos em seu disco rígido e envie anexos de e-mail cifrados.
Mailvelope é de código aberto e com base em OpenPGP.js (https://openpgpjs.org), uma biblioteca OpenPGP para JavaScript.
Uma introdução é dada em https://casalribeiro.com/pt/email-encryption-mailvelope/ .
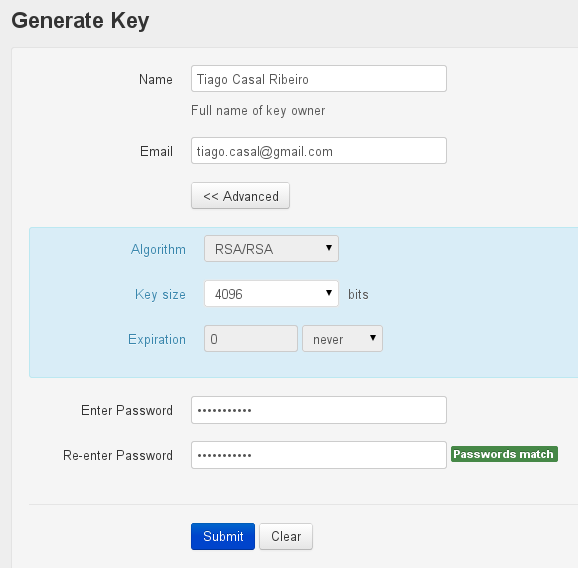
Mailvelope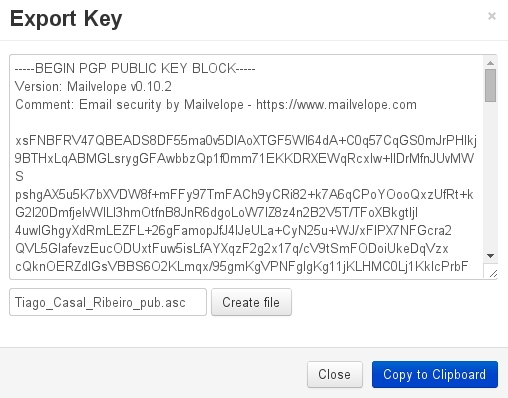
MailvelopeÉ muito confortável, porém, este conforto vem ao detrimento da segurança; consta-se que
XSS, em que um site acede aos dados locais armazenados para outro);Javascript em que a extensão é escrita não é apropriada para uma cifração segura; entre outros, é suscetível às seguintes falhas :
Por isso, é mais seguro usar um cliente de e-mail, como Thunderbird com Enigmail. Em seguida, para proteger as chaves da melhor forma, um cartão inteligente, como sera apresentado no fim deste capítulo.
Todo programa que será apresentado (Autocrypt ou prettyeasyprivacy ou Delta-Chat) não é uma solução perfeita, mas conforme a RFC 7435 (Request for Comments, padrão livremente criado pelos usuários na internet) oferece apenas “Opportunistic Security: Some Protecion Most of the Time”: Opportunistic Security significa uma proteção contra atacantes passivos, mas não contra atacantes ativos; isto é, a cifração da comunicação funciona só enquanto ninguém se interesse nela! Justamente pela falta da verificação do dono da chave privada que corresponde à chave pública, é vulnerável ao ataque “man-in-the middle” (MITM) em que o atacante se interpõe entre as duas partes que se comunicam; Por exemplo, é perfeitamente possível
WhatsApp.A cifração da comunicação apenas impede que é lida por terceiros, mas não garante que a conta pertença à pessoa alegada. Para evitar este ataque, tem que verificar pessoalmente (ou por outro canal, por exemplo, por telefone) com o dono o “fingerprint” (= impressão digital = uma soma de verificação criptográfica) da sua chave pública.
AutocryptNa versão 2.0 a extensão Enigmail tem suporte para o programa Autocrypt que automatiza a troca de chaves públicas: Ele insere uma linha adicional no cabeçalho do e-mail (que é normalmente invisível para o usuário) que contém o certificado (nome, endereço de e-mail e referência à chave pública do usuário). Autocrypt foi iniciado por um projeto da União Europeia em resposta às revelações por Edward Snowden.

AutocryptEm vez disto, o envio automático da chave pública de Alice, um melhor funcionamento seria:
prettyeasyprivacyOutro projeto para mandar e-mails cifrados automaticamente como Autocrypt, fundado por uma iniciativa privada, que dá suporte a programas comerciais como o cliente de e-mail (e agendador, entre outros) Microsoft Outlook é prettyeasyprivacy.
Instala e lança mão de GPG(4Win), isto é, é uma interface gráfica no cliente de e-mail para este programa.
Uma ideia interessante é usar Safewords (palavras seguras) em vez da codificação hexadecimal para verificar a impressão digital de uma chave pública, isto é,
72F0 5CA5 0D2B BA4D 8F86 E14C 38AA E0EB,Oceania contaminação arenas gogo ema; o que é bem mais apto para nos seres humanos.Delta-ChatMais um projeto semelhante, para mandar mensagens instantâneas automaticamente cifradas para outros usuários, é o aplicativo Delta-Chat que usa a conta de e-mail do usuário.
Como usa o mesmo protocolo aberto como o e-mail, em comparação a muitos outros aplicativos para mandar mensagens instantâneas automaticamente cifradas (como WhatsApp), não depende dos servidores de uma empresa específica. (Dizem que tem suporte a federação, por exemplo, um usuário de hotmail.com pode comunicar com outro de gmail.com.) Esta dependência traz os seguintes problemas:
facebook.com),WhatsApp aconteceu no Brasil e na China),Além disso, é compatível a destinatários que não usam o Delta Chat porque podem ser contatados por e-mail.
Isto dito, os meta-dados entre os servidores de e-mail não são cifrados. (O protocolo de e-mail IMAP é antigo e tem muitas deficiências; porém, é o estabelecido padrão, testado pelo tempo, com um grande ecossistema de programas.)
O mensageiro Conversations propõe um protocolo moderno XMPP que usa menos meta-dados que o protocolo IMAP. (Aparenta que o mensageiro Signal use menos meta-dados que Conversations, mas infelizmente quase todos os servidores são mantidos pela própria fornecedora Open Whisper Systems, em contraste ao Conversations. No fim das contas, a única solução segura é rodar o seu próprio servidor!)
É uma solução bastante completa quanto à segurança; infelizmente pouco estabelecida; por exemplo, há muitos servidores de e-mail (isto é, que comunicam pelo protocolo IMAP); porém, pouquíssimos que comunicam por XMPP.
Explicamos a utilidade da aritmética modular na criptografia: Lembremo-nos que a função alçapão é facilmente computável, porém o seu inverso (por exemplo, a radiciação no RSA) é quase incomputável!
É esta dificuldade de calcular o inverso que corresponde à dificuldade da decifração, de inverter a cifração.
Os algoritmos criptográficos assimétricos como o RSA usam
Os algoritmos criptográficos, como o RSA, usam a aritmética modular para dificultar a computação da função inversa da potenciação, a radiciação. Já conhecemos a aritmética modular ou circular! Pela aritmético do relógio, onde um número fixo , por exemplo no caso do relógio, é considerado igual a . Como o indicador recomeça a contar a partir de após cada volta, por exemplo, horas após horas são horas: Sobre este domínios, chamados de anéis finitos, (os gráficos d’) estas funções tornam-se irregulares e praticamente incomputáveis, pelo menos sem conhecimento de um atalho, a chave.
A seguir,
A dificuldade de calcular o inverso corresponde à dificuldade da decifração, de inverter a cifração. Na criptografia assimétrica,
baseiam-se em uma função invertível tal que
Por exemplo, os inversos das funções alçapão
Diffie-Hellman), eRSA)são dados pela
Observação. Observamos que as funções usadas são ambas algébricas, isto é, exprimem-se por uma fórmula (de somas, produtos e potências) finita. Funções analíticas, isto é, somas infinitas convergentes, por exemplo, o seno, cosseno, …, parecem impraticáveis pelos erros que surgem do necessário arredondamento.
Eles são
Introduzamos estes domínios:
O seu domínio não é o dos números inteiros (ou o dos números reais que os contém), porque ambas as funções, exponenciação e potenciação, são contínuas sobre :
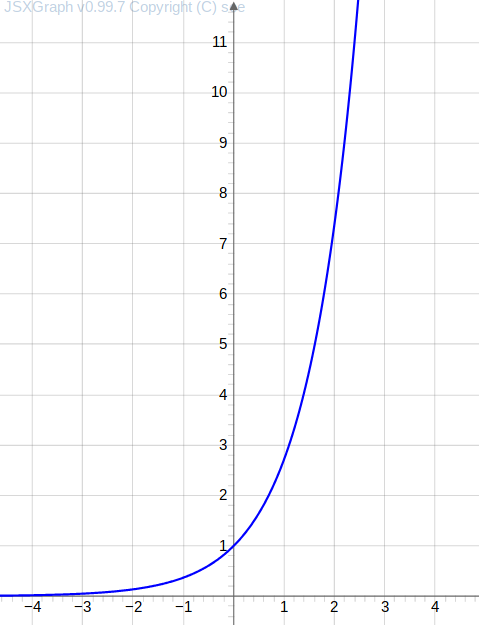
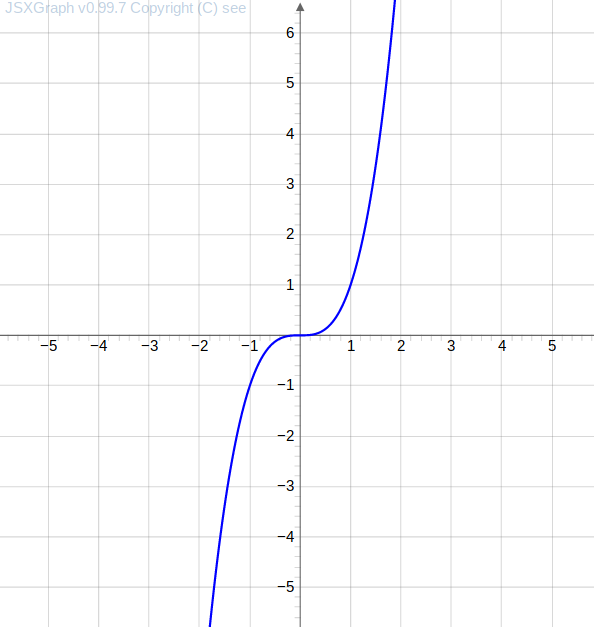
Se o domínio destas funções fosse , os seus inversos poderiam ser aproximados sobre , por exemplo, pelo Método da Bisseção: Dado , encontrar um tal que equivalha encontrar um zero da função
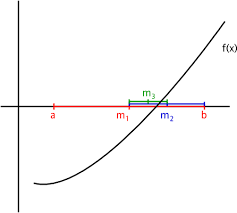
Pelo Teorema do Valor Intermediário, o zero é garantido de estar no intervalo, que a cada passo diminui e converge à interseção.
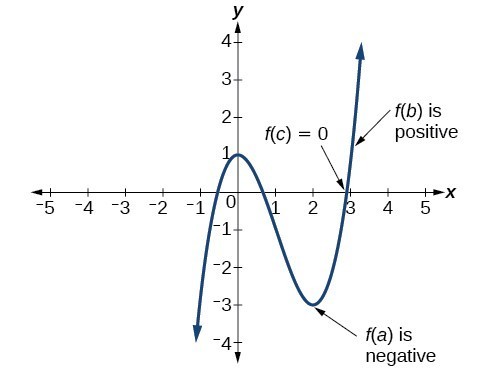
Bisseção do polinômio com pontos iniciais e
| Step | x | F(x) | |
|---|---|---|---|
| 0 | 8 | 5 | |
Para evitar a iterada aproximação ao zero e assim dificultar a computação da função inversa (além de facilitar a computação da função mesma), o domínio de uma função alçapão é um anel finito (= principalmente um conjunto finito que contém e e sobre que uma soma é definida) para um número natural . Neles, vale e toda adição (e logo toda multiplicação e toda potenciação) tem resultado . Assim é como anel não incluso em . Por exemplo, para , Introduziremos estes anéis finitos primeiro pelos exemplos e (= os anéis dos números das horas do relógio e dos dias da semana), depois para qualquer.
Quando olhamos as funções, cujos gráficos são tão regulares em , no anel finito ,
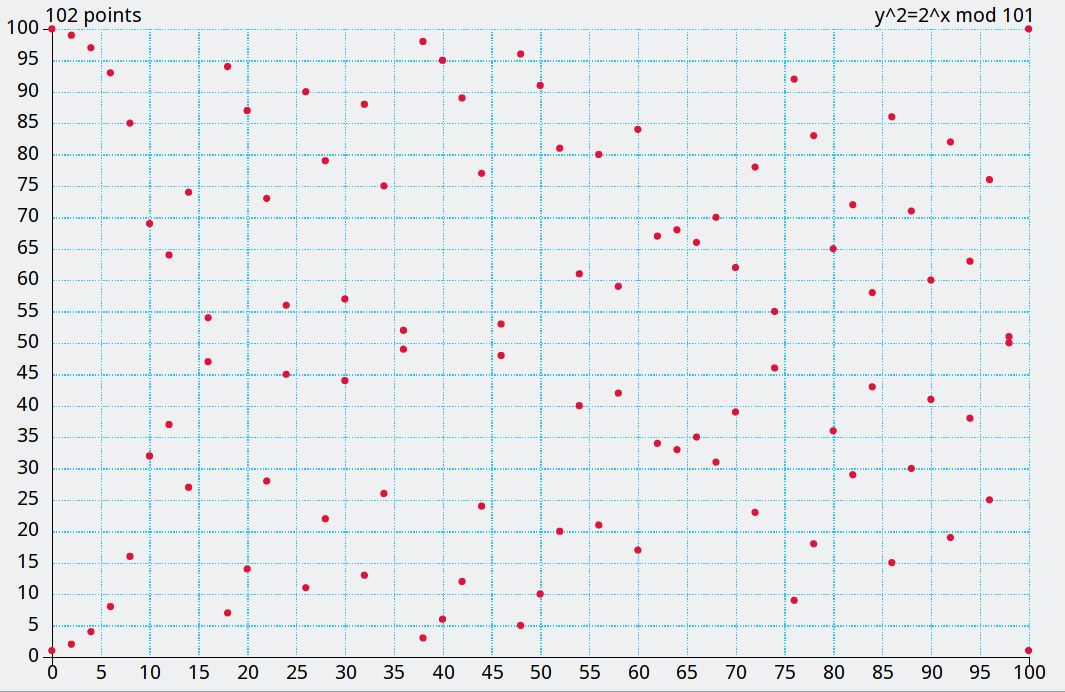
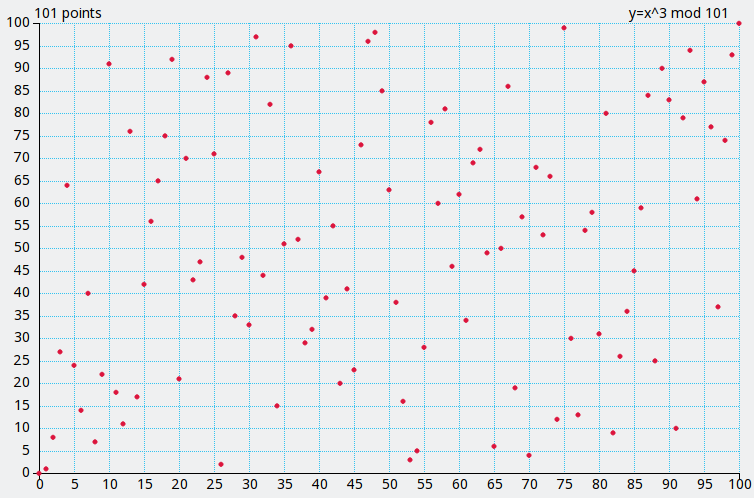
observamos que
é inicialmente tão regular sobre quanto sobre , mas
começa a comportar-se erraticamente (exceto a formosa simetria da parábola no eixo central pela igualdade ).
Invitamos o caro leitor a experimentar com este plotter em linha de gráficos de funções discretos (de que origina a imagem acima), uma cortesia de Sascha Grau.
Observação: Observamos que dependente da base da exponenciação e do expoente da potência , a função pode só ser invertível sobre subconjuntos do seu domínio e contra-domínio, isto é, dos seus argumentos e valores.
Para invertê-la, na sua imagem (= o conjunto dado por todos os seus valores), ela precisa de ser injetora (isto é, manda argumentos diferentes a valores diferentes).
A imagem da exponenciação nunca contém e é possivelmente menor ainda do que . Para sobre , a sua imagem é máximo, quer dizer, é ; em outras palavras, todos os números (diferentes de zero) são potências de . (Diz-se que gera .) Porém, por exemplo gera sobre o mesmo domínio só a metade de , isto é, um conjunto de elementos. Seção 7.2 mostrará que existe um gerador de se, e tão-somente se,
Se o expoente é par, para um inteiro , então a potenciação satisfaz , isto é, manda e ao mesmo valor. Em particular, não é injetora. Observamos esta simetria para sobre em Figura 5.3 ao longo do eixo central (e também que a sua restrição a é injetora).
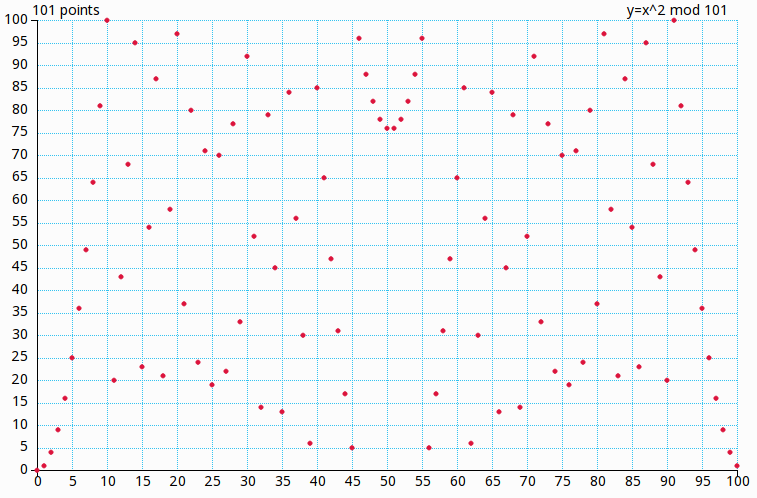
Dado um módulo , Seção 7.2 mostrará para quais expoentes a potenciação é injetora sobre :
RSA), são os sem divisor comum nem com , nem com . Por exemplo, para , o expoente .Vale a pena verificá-lo pelo plotter.
Introduzamos esses domínios finitos (o anel dos inteiros módulo , para um número natural (comumente primo) ) das funções alçapão na criptografia assimétrica; são eles que dificultam tanto a nossa vida quando tentamos invertê-la (em comparação a ou ).
Veremos que já os conhecemos e usamos no dia-a-dia para , na aritmética do relógio, e para , nos dias da semana.
Recordemo-nos breve da Divisão com Resto:
Definição. Sejam e números inteiros positivos. Que dividido por tem resto significa que existe um inteiro tal que Exemplo. Para e , obtemos . Isto é, o resto de dividido por é .
Para um número inteiro qualquer, definiremos o anel finito (= para nós sobretudo um conjunto finito em que podemos somar) como segue:
Damos exemplos da aritmética modular do nosso dia-a-dia (como o relógio, os dias da semana, ou até o alfabeto). A propriedade comum entre estes exemplos é a sua circularidade (de onde a nomenclatura “anel”).
O exemplo protótipo de aritmética modular é a aritmética do relógio em que o ponteiro volta após horas no início; isto é, vale a equação que implica, entre outros, as equações Quer dizer, horas depois das horas é hora, e horas antes da hora são horas. Podemos ir mais longe: quer dizer se agora são horas, então horas (= um dia) mais tarde também.

Além das horas, outro exemplo do aritmética modular no dia-a-dia são os dias da semana: tendo passado dias, os dias da semana recomeçam. Se numeramos sábado, domingo, segunda, terça, quarta, quinta e sexta-feira por , , , , , , então vale a equação e que implica, entre outros, as equações Quer dizer, dias depois da quarta-feira é domingo, e dias antes do domingo é sexta-feira. Podemos ir mais longe: , quer dizer se agora é quinta-feira, então daqui em dias (= duas semanas) também.
Além das semanas, outro exemplo do aritmética modular no dia-a-dia são os meses do ano: tendo passado meses, os meses do ano recomeçam. Se numeramos janeiro, fevereiro, … por , , … então vale, como no relógio, a equação e que implica, entre outros, as equações Quer dizer, um trimestre depois outubro recomeça o ano, e meses antes de janeiro é novembro. Podemos ir mais longe: , quer dizer se agora é maio, então daqui em anos também.

Na cifração de César, trasladamos cada letra do alfabeto por uma distancia fixa; por exemplo, para , obtemos Para trasladarmos as últimas letras , e do alfabeto, consideramos o alfabeto como anel, isto é:
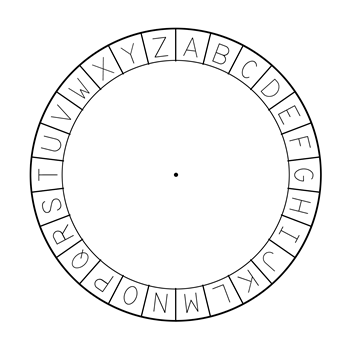
Assim, Se identificamos cada letra do alfabeto romano com a sua posição, então vale , e ; isto é, .
Formalmente, derivamos as equações em e das igualdades e
Em geral, para quaisquer e em , ou, equivalentemente, para quaisquer e em , Em palavras, e deixam o mesmo resto divido por .
As mesmas observações valem para os dias da semana.
Não há nada de especial sobre o número (horas até meio-dia), (dias da semana) ou (letras do alfabeto latino). Por exemplo, as mesmas observações valeriam se o relógio indicasse horas (como no planeta Netuno em que o dia, a rotação completa em torno do próprio eixo, dura horas):

Definição. Seja um inteiro. Os números inteiros e são congruentes módulo ou, em fórmulas, se , isto é se a sua diferença é divisível por . Em outras palavras, se e deixam o mesmo resto divido por . O número é o módulo.
Exemplo: Para a cifração de César, sejam
A cifração e decifração se descrevem pelo aritmética modular por
Dado um inteiro , queremos construir um conjunto com e e sobre que podemos somar (isto é, existe uma operação ) tal que nele valha (Já observamos que, para esta igualdade valer, sobre tem de ser definida diferente de sobre .) Além do conjunto, queremos construir uma aplicação (ou talvez melhor identificação) tal que se, e tão-somente se, . Isto é, identifica e se têm o mesmo resto divido por .
Um tal conjunto chama-se anel (comutativo com ). Mais exatamente, é
Queremos construir de duas formas, prática e teórica,
Para o matematicamente interessado, a propriedade definidora do anel é que ele seja
Observamos que, por exemplo,
Matematicamente, a propriedade definidora da minimidade do anel é uma propriedade universal: Qualquer aplicação que satisfaz passa pela aplicação ; isto é, sempre há uma aplicação tal que
Esta é a construção encontrada em livros de matemática (universitária).
Equação diz que exatamente , e consequentemente, para em qualquer, exatamente O que nos leva a pôr
como conjunto e como aplicação
como elementos neutros da adição e multiplicação
como operações e (Diante da definição da identificação , esta definição de é requerida pela igualdade .)
Esta é a construção encontrada em livros de ciências que aplicam a matemática (por exemplo, a ciência da computação).
Pomos
como conjunto e como aplicação
como elementos neutros da adição e multiplicação
como operações e e
Isto é, para adicionar e multiplicar em ,
Pela definição da identificação como resto divido por , a igualdade requer que a soma dos restos seja definida pelo resto da soma.
Por exemplo, para obtemos as tabelas de adição e multiplicação
| + | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
e
| * | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 0 | 2 |
| 3 | 0 | 3 | 2 | 1 |
Exercício. Mostra que um número inteiro é divisível por (respectivamente ) se, e tão-somente se, a soma dos seus algarismos decimais é divisível por (respectivamente ).
Em Python, o operador modular é denotado pelo símbolo percentual %. Por exemplo, na shell interativa, obtemos:
A função alçapão
RSA é uma potenciação , eElGamal (baseado na troca de chaves de Diffie-Hellman) é a exponenciação em para um número natural . Vemos como calculá-la eficazmente:
Dados uma base e um expoente em , para calcular
Como , isto é, cada potência é o quadrado da anterior (e no máximo ), cada uma, sucessivamente, é facilmente computável. Obtemos Isto é, apenas as potências com expoentes iguais a importam, as outras podem ser omitidas.
Este algoritmo leva multiplicações módulo .
Para calcular módulo , expandimos e calculamos obtendo
Para calcular módulo , expandimos e calculamos obtendo
Para já nos convencermos da utilidade da aritmética modular, olhamos o protocolo para construir uma chave secreta mútua através de um canal inseguro, apresentado pela primeira vez em Diffie e Hellman (1976).
Isto não é exatamente criptografia assimétrica, ou criptografia de chave pública, porque a chave secreta é conhecida a ambos os correspondentes. Os alogritmos assimétricos que se baseiam neste protocolo (por exemplo, ElGamal e ECC) geram uma chave de uso único para cada mensagem. Esta geração tem de ser suficientemente aleatória para ser imprevisível.
Observação. Denote daqui por diante, num algoritmo de criptografia assimétrica,
Para Alice e Bob construírem uma chave secreta através de um canal inseguro, combinam primeiro
e depois
O CrypTool 1 oferece no Menu Individual Procedures -> Protocols uma entrada para experimentar com os valores das chaves no Diffie-Hellman.
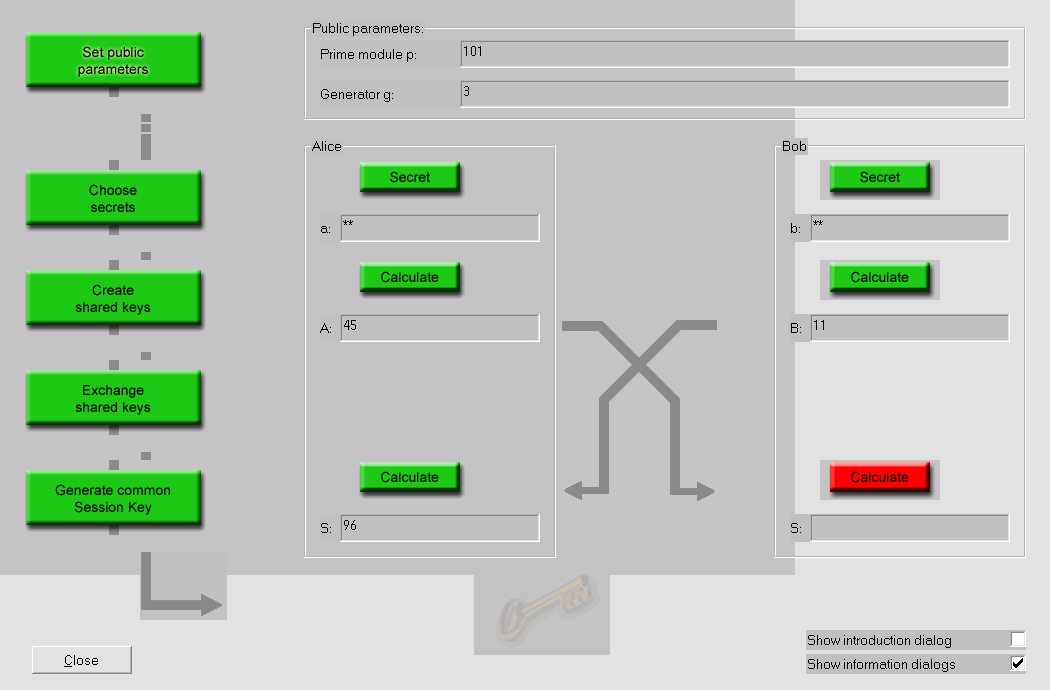
Diffie-Hellman no CrypTool 1Em Seção 8, o algoritmo ElGamal mostra como cifrar uma mensagem pela chave mútua (que constrói uma chave mútua efêmera por cada mensagem cifrada).
A segurança da troca de chaves de Diffie-Hellman reside na dificuldade de computar o logaritmo módulo .
Um olheiro obteria a chave secreta a partir de e , se pudesse computar isto é, o logaritmo inverte a exponenciação ,
Enquanto a exponenciação é facilmente computável, o logaritmo é dificilimamente computável para escolhas de e apropriadas, isto é:
Concluímos que, como e são públicos, a segurança computacional de Diffie-Hellman baseia-se unicamente na dificuldade da computação do logaritmo módulo .
Mais exatamente, a segurança da Troca de Diffie-Hellman baseia-se no problema de Diffie-Hellman Computacional. Os três problemas da computação do logaritmo modular são, em ordem descendente da sua dificuldade:
O problema do Logaritmo Discreto: Dado , calcula tal que .
Uma solução seria um algoritmo que leva tempo polinomial em (o número de bits de) para calcular .
O problema de Diffie-Hellman Computacional: Dados e (mas não e ), calcula .
Uma solução seria um algoritmo que leva tempo polinomial em (o número de bits de) e para calcular .
O problema de Diffie-Hellman Decisório: Dados e , decide se , e para alguns e (que não precisam ser encontrados) ou não.
Uma solução seria um algoritmo BPP (= bounded error probabilistic polynomial time) que leva tempo polinomial em (o número de bits de) , e para decidir com uma probabilidade de erro se , e para alguns e . (Pela repetição do algoritmo e a escolha do resultado mais frequente, a probabilidade de erro pode ser diminuída a um valor arbitrariamente pequeno em tempo polinomial.)
O primeiro problema é mais difícil do que o segundo, e o segundo e mais difícil que o terceiro; isto é: A solução do primeiro problema implica a do segundo, e a do segundo implica a do terceiro. Ou, equivalentemente, a hipótese da solução do terceiro problema implica a do segundo, e a do segundo implica a do primeiro.
Se o grupo que contém é genérico (isto é, satisfaz apenas os axiomas de um grupo, mas nada além) e de cardinalidade prima ou desconhecida, então se demonstra que não existe solução do problema de Diffie-Hellman Decisório, logo, tampouco para os problemas de Diffie-Hellman Computacional e o Logaritmo Discreto. Porém, isto não exclui que exista solução em grupos específicos tal como das unidades multiplicativas módulo um primo ; o que de fato ocorre!
Vice-versa: Toda solução conhecida do segundo problema se baseie na solução do primeiro; logo, supõe-se que, de fato, estes dois problemas sejam equivalentes, isto é, a solução do primeiro problema implique a do segundo, e reciprocamente. Existem evidências: Joux e Nguyen (2003) constrói uma família de grupos onde eles são equivalentes e, supostamente, irresolúveis (como definido acima). Antes, em 2001, Maurer e Wolf (1999) já demonstrou esta equivalência para grupos genéricos (baseado em observações para curvas elípticas finitas no início dos anos 90) com certas restrições nos divisores primos da cardinalidade do grupo.
Ao contrário, o terceiro problema é para muitos grupos mais fácil do que o segundo, isto é, existem grupos conhecidos em que o problema Diffie-Hellman Decisório é resolúvel, mas não o problema de Diffie-Hellman Computacional. (Este é um fenómeno não tão desconhecido: Por exemplo, enquanto leva tempo exponencial (no número de bites) para calcular os fatores primos de um número composto , existem algoritmos que levam tempo polinomial para decidir se é composto sem revelar os seus fatores. De fato, conjetura-se que todo algoritmo BPP, cuja saída pode ser verifica em tempo polinomial com probabilidade de erro , é um algoritmo em P, os cuja saída pode ser verifica em tempo polinomial. Foi demonstrado em 2002 por Agrawal, Kayal e Saxena, um algoritmo polinomial existir para a verificação se um número é primo ou não, isto é, ser em P; antes, por exemplo, o Teste de Rabin-Miller, já mostrou que o problema é em BPP. [Na prática, o Teste de Rabin-Miller permanece o algoritmo preferido porque é muito mais rápido e a probabilidade de erro arbitrariamente pequena.])
O exemplo clássico e importante, de um grupo em que o problema de Diffie-Hellman Decisório é resolúvel: se gera todo o grupo (isto é, para pela primeira vez) então o valor de em revela se é par ou ímpar. Isto é, dados , e , calculam-se em tempo polinomial (no número de bits) os bits menos significativos de , e ; logo, consegue-se pela sua comparação distinguir de um número qualquer em tempo polinomial com probabilidade de erro . Isto é, o problema é resolúvel segundo a definição dada acima.
O exemplo clássico, de um grupo em que o problema de Diffie-Hellman Decisório é supostamente irresolúvel segundo muitos criptologistas, é um subgrupo de cardinalidade prima de para primo. Por exemplo, se é primo, (isto é, é um primo seguro), então o grupo de quadrados módulo é um tal grupo.
Observação. A criptografia baseada em emparelhamentos (pairing-based cryptography) usa (os grupos de) curvas elípticas finitas especialmente criadas em que o problema de Diffie-Hellman Computacional seja considerado difícil, mas o de Diffie-Hellman Decisório seja fácil. Isto é, outra indicação da suposta inequivalência entre eles.
Ele foi popularizada por Antoine Joux em 2002, e usa certo emparelhamento de Weil na curva elíptica para, por exemplo, estabelecer um segredo comum entre três participantes (enquanto a Troca de Chave segundo Diffie-Hellman é restrita a dois): O emparelhamento é bilinear, isto é, . Se a Alice partilha , o Bob partilha e o Charles partilha para um inteiro aleatório e secreto , então
Pela bilinearidade, todos os valores são iguais. (Nota que denota um ponto na curva, um par de números e a potenciação é a iterada adição deste ponto no grupo como explicado em Seção 9.3.)
Teorema de Euclides. Demonstração: Suponhamos o contrário, que haja só um número finito de números primos. Considere . Como é maior que , …, , não é primo. Seja então um número primo que divida . Pela hipótese, em . Porém, pela sua definição, tem o resto divido por qualquer primo , …, . Contradição!
O Teorema de Euclides garante que haja números primos arbitrariamente grandes ( bites). Em Seção 7.3, veremos como encontrá-los. Graças a Deus, quase todo número primo satisfaz que
O Teorema da Raiz Primitiva (que será demonstrado em Seção 7.2) garante que sempre haja um número em tal que Em particular, a cardinalidade de é um múltiplo de qualquer divisor primo de .
Na prática, os números e são adotados duma fonte confiável.
Como inicialmente os valores sobre igualam os valores de sobre , mais exatamente para (por exemplo, em Figura 5.1 com e para ), os números secretos e devem ser suficientemente grande, mais exatamente, maior do que . Para garantir isto na prática, estes números são artificialmente aumentados (por exemplo, se obtidos a partir de uma mensagem demasiada curta, ela é artificialmente enchida).
Presentemente, o algoritmo mais rápido para calcular o logaritmo a partir de , é uma modificação do campo de número de peneira geral de Gordon (1993). A grosso modo, o número de operações para calcular o logaritmo de um número inteiro de bites é
Observemos para módulos que não são primos, isto é, um produto de fatores primos, que a dificuldade aumenta linearmente no número dos fatores, ao contrário dela aumentar exponencialmente no número dos bites de cada fator:
Se o módulo é produto de dois fatores e sem fator comum, então o logaritmo modular pode ser computado, pelo Teorema Chinês dos Restos, pelos logaritmos Mais exatamente, existem inteiros e , computados (em tempo linear no número dos bites de e ) pelo Algoritmo de Euclides (estendido), tais que e
Se o módulo é uma potência de um primo , então Bach (1984) mostra como o logaritmo modular módulo para uma base pode ser computado em tempo polinomial a partir do logaritmo módulo . Exponhamos os passos para um número primo :
Recordemo-nos da subsecção sobre a existência da raiz primitiva para qualquer módulo de Seção 7.2 que é cíclico de ordem . Logo, existe uma aplicação multiplicativa dada por onde denote o grupo das -ésimas raízes da unidade e o das unidades unitárias.
Temos o isomorfismo dado por e o seu inverso por para qualquer em tal que . (Observa que a restrição do homomorfismo dado por a é a identidade porque a ordem de é .)
Temos o logaritmo para a base e temos o logaritmo natural que é calculado em tempo polinomial pela fórmula e o qual fornece o logaritmo para a base pelo escalamento
Pelo Teorema Chinês dos Restos, temos o isomorfismo dada pelo produto e o seu inverso dado por onde e satisfazem e foram obtidos pelo Algoritmo de Euclides (estendido).
Concluímos que, dado
o valor de é computado em tempo polinomial.
Observação. Para facilitar a computação, ao invés da projeção dada em por , é mais rápido usar a dada por . Porém, a sua restrição a não é a identidade. Logo, é preciso usar ao invés de o logaritmo escalado para obter
Fundamentemos a Equação 6.1 que define o logaritmo : recordemos a definição da exponencial sobre pelos juros compostos a qual leva à definição da função inversa onde .
Ora, em , temos , , , …, , isto é, , o que talvez motive a ideia de considerar como pequeno. Logo, o bom análogo sobre é Com efeito, sobre é um valor bem-definido em , porque se divide , então nenhum denominador da fração cortada é divisível por e todos os números indivisíveis por são invertíveis em . Da mesma maneira, sobre , é um valor bem definido em , porque se divide , então nenhum denominador cortado é divisível por e todos os números indivisíveis por são invertíveis em .
De interesse particular é a base do logaritmo natural em , isto é, o argumento tal que . Por exemplo, para e , calculamos
Estudamos a multiplicação nos anéis finitos . Interessamo-nos em particular por quais números podemos dividir neles. Será o Algoritmo de Euclides que nos computa a reposta.
A chave privada
RSA, ouElGamal (baseado na troca de chaves de Diffie-Hellman),define uma função que é o inverso da função definida pela chave pública. Este inverso é computado via o maior divisor comum entre os dois números. Este, por sua vez, é computado pelo Algoritmo de Euclides, uma iterada divisão com resto.
Introduzimos então
Sejam e números inteiros. Denotamos por que divide , isto é, que é um múltiplo de (existe um inteiro tal que ). Recordemo-nos de umas implicações básicas sobre a divisibilidade entre números inteiros:
Proposição 1. Sejam números inteiros.
Definição. Um divisor comum de dois números inteiros e é um número natural que divide os dois. O maior divisor comum de dois números inteiros e é o maior número natural que divide os dois. Denote o maior divisor comum de e ,
Exemplo. O maior divisor comum de e é .
Definição. Os números inteiros e são relativamente primos se , isto é, se nenhum número inteiro divide e .
Para quaisquer números inteiros e , os números inteiros e para são relativamente primos.
A divisão com resto ajuda-nos a construir um algoritmo eficiente para calcular o maior divisor comum. Recordemos-nos, mais uma vez Divisão com Resto:
Definição. Sejam e números inteiros positivos. Que dividido por tem quociente e resto significa
Exemplo. Para e , obtemos . Isto é, o resto de dividido por é .
Uma combinação linear (ou soma de múltiplos) de dois números inteiros e é uma soma para números inteiros e .
Exemplo. Para e , uma soma de múltiplos deles é
É importante observar pela Proposição 1.C a seguinte implicação: se um número inteiro divide e , então divide toda combinação linear de e .
Em particular, olhando à divisão com resto em Equação 7.1, para um número inteiro , observamos:
Isto é, divide e se, e tão-somente se, divide e . Quer dizer, os divisores comuns de e são os mesmos que os de e . Em particular, Dividindo com resto os números e (que é ), obtemos e Iterando, e assim diminuindo o resto, chegamos a e com , isto é Em palavras, o maior divisor comum é o penúltimo resto (ou o último diferente de ).
Exemplo. Para calcular , obtemos
logo .
O CrypTool 1, na entrada do menu Indiv. Procedures -> Number Theory Interactive -> Learning Tool for Number Theory, Seção 1.3, página 15, mostra uma animação deste algoritmo:
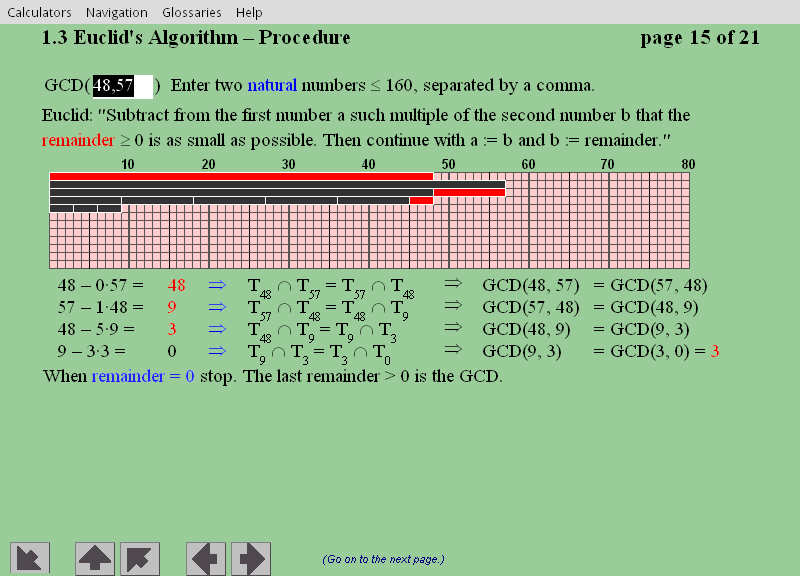
CrypTool 1Formalizemos o que acabamos de observar:
Teorema. (Algoritmo de Euclides) Sejam e números inteiros positivos com . O seguinte algoritmo calcula em um número finito de passos:
(início) Ponha e , e .
(divisão) Divida por com resto para obter (distinção) Distinga entre:
Demonstração: Precisamos de demonstrar que o algoritmo termina com o maior divisor comum de e :
Como , finalmente para suficientemente grande, e o algoritmo termina.
Pela Equação 7.1, temos Como ultimamente para suficientemente grande, temos Isto é, .
Observação: Bastam divisões com resto para o algoritmo terminar.
Demonstração: Demonstramos Temos
Neste último caso, segue e então Por () obtemos iterativamente que bastam divisões com resto para o algoritmo terminar.
Com efeito, revela-se que já bastam no máximo divisões com resto, e em média já .
Para a computação do inverso modular, precisamos de mais informações do que o maior divisor comum (calculado pelo Algoritmo de Euclides).
Com efeito, observa-se que em cada passo do Algoritmo de Euclides o maior divisor comum de e é uma combinação linear (ou soma de múltiplos) de e , isto é, O inverso de módulo é um destes múltiplos. Vamos apresentar o Algoritmo de Euclides Estendido que preserva esta informação.
Teorema. (Algoritmo de Euclides Estendido) Para quaisquer números inteiros positivos e , o seu maior divisor comum é uma combinação linear de e ; isto é, há números inteiros e tais que Demonstração: Como , , e , segue que é uma combinação linear de e . Em geral, como e são combinações lineares de e , primeiro é uma combinação linear de e , e assim é uma combinação linear de e . Em particular, se então é uma combinação linear de e .
O CrypTool 1, na entrada do menu Indiv. Procedures -> Number Theory Interactive -> Learning Tool for Number Theory, Seção 1.3, página 17, mostra uma animação deste algoritmo:
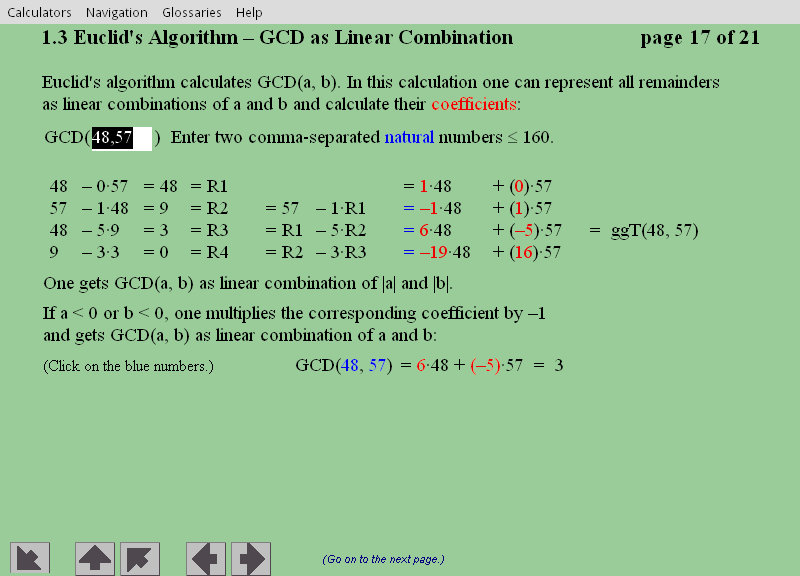
Exemplo. Revenhamos à calculação do maior divisor comum de e . O algoritmo de Euclides deu:
,
o que fornece as combinações lineares
.
Com efeito,
PythonPara implementar o algoritmo de Euclides, vamos usar atribuição múltipla em Python:
>>> spam, eggs = 42, 'Hello'
>>> spam
42
>>> eggs
'Hello'
>>> a, b, c, d = ['Alice', 'Bob', 'Carol', 'David']
>>> a
'Alice'
>>> b
'Bob'
>>> c
'Carol'
>>> d
'David'Os nomes das variáveis e os seus valores são alistados à esquerda respectivamente à direita de .
Aqui é uma função que implementa o algoritmo de Euclides em Python; ela devolve o maior divisor comum de dois inteiros e .
Por exemplo, no shell interativo:
O operador // vai figurar na implementação do algoritmo de Euclides estendido; ele divide dois números e arredonda para baixo. Isto é, devolve o maior inteiro igual ou menor que o resultado da divisão. Por exemplo, no shell interativo:
Optamos pela seguinte implementação do algoritmo de Euclides estendido:
def egcd(a, b):
x,y, u,v = 0,1, 1,0
while a != 0:
q, r = b//a, b%a
m, n = x-u*q, y-v*q
b,a, x,y, u,v = a,r, u,v, m,n
gcd = b
return gcd, x, yPor exemplo,
A chave privada é calculada pelo inverso multiplicativo na aritmética modular a partir da chave pública, tanto no algoritmo RSA quanto no algoritmo ElGamal.
Acabamos de apreender como calcular o maior divisor comum pelo Algoritmo de Euclides Estendido; agora apreendamos como ele é usado para calcular este inverso multiplicativo.
Enquanto em podemos dividir por qualquer número (exceto ), em unicamente por ! Os números pelos quais pode se dividir são chamadas invertíveis ou unidades. A quantidade de números invertíveis em depende do módulo . De modo grosso, quanto menos fatores primos em , tanto mais unidades em .
Definição. O elemento em é uma unidade (ou invertível) se existe em tal que . O elemento é o inverso de e denotado por . O conjunto das unidades (em que podemos multiplicar e dividir) é denotado por A função totiente de Euler é isto é, dado , conta quantas unidades tem.
Observações:
Exemplos:
No relógio, isto é, para a multiplicação de uma hora por corresponde a iterar vezes o caminho percorrido pelo indicador em (a partir de .) Observamos que para e existe uma iteração do caminho que leva o indicador a (mais exatamente, feita , , e vezes), enquanto para todos os outros números, esta iteração leva o indicador a . Estas possibilidades são mutuamente exclusivas, e concluímos Isto é, .
Nos dias da semana, isto é, para , obtemos Isto é, o número de unidades é tão grande quanto possível, isto é, , todos os números exceto .
Para , a tabela de multiplicação
| * | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | 0 | 2 | 0 | 2 |
| 3 | 0 | 3 | 2 | 1 |
mostra pois e em . Ao contrário, em , em particular não é uma unidade. (Mas um divisor de zero; de fato, cada elemento em é ou uma unidade, ou um divisor de zero.) Logo .
Para , a tabela de multiplicação
| * | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
revela as unidades .
Proposição. Seja em e em , isto é, em . O número é uma unidade em se, e tão-somente se, .
Demonstração: Observamos que cada divisor comum de e divide cada soma de múltiplos de e ; em particular, se , então o maior divisor comum de e é .
Pelo Algoritmo de Euclides Estendido, há e em tais que Logo, pela observação acima, se, e tão-somente se, há em tal que Equivalentemente, para em o resto de dividido por . Isto é, é uma unidade em cujo inverso é .
Observação. Concluímos que para em com , obtemos pelo Algoritmo de Euclides Estendido e em tais que O inverso de em é dado pelo resto de dividido por .
Em Python, podemos então calcular o inverso de em por
def ModInverse(a, m):
if gcd(a, m) != 1:
return None # no mod. inverse exists if a and m not rel. prime
else
gcd, x, y = egcd(a,m)
return x % mCorolário 7.1. Se é um número primo, então
Isto é, todos os elementos, exceto , são unidades. Em particular, .
Demonstração: Se é primo, então para qualquer em .
Um anel cujos elementos, exceto , são todos unidades é um corpo. Isto é, em um corpo, dado um elemento , além de , o inverso de sob adição, sempre há , o inverso de sob multiplicação. Em vez de , se escreve também . Em outras palavras, além de podermos subtrair, podermos dividir. Os exemplos mais comuns são , e , todos sendo infinitos.
O corpo com elementos (isto é, ) é denotado por .
Observação. Para um módulo do tipo para e primo, vale pelo Teorema Chinês dos Restos , e conforme Em particular, como os dois fatores são corpos, . Esta observação é (implicitamente, neste curso) usada no algoritmo RSA.
Teorema. (Existência da raiz primitiva em um corpo finito) Se é um número primo, então existe em tal que
Demonstração: Como (pela iterada divisão com resto) um polinômio de grau tem raízes, e se, e tão-somente se, para , vale
Mostramos que qualquer tal grupo é cíclico, isto é, gerado por um elemento: Seja um elemento em de ordem (= o menor número tal que ) máxima. Se , então há por um em cuja ordem não divide . Então a ordem de é , em contradição à escolha de .
Para explicarmos porque usualmente só módulos primos são usados para Diffie-Hellman, estabeleçamos para quais módulos as unidades de têm um único gerador:
Proposição. Se é um número primo e um inteiro positivo, então em é uma unidade se, e tão-somente se, não divide .
Demonstração: O número em é uma unidade se, e tão-somente se, a multiplicação sobre é sobrejetora, isto é, todo elemento em é produto de . Como é finito, pelo princípio do pombal, uma aplicação sobre é sobrejetora se, e tão-somente se, é injetora, isto é, manda dois argumentos diferentes a dois valores diferentes.
Como a multiplicação sobre satisfaz , ela é injetora se, e tão-somente se, para todo em , se , então .
Por contraposição, existe em não-nulo com , isto é, não divide , mas divide se, e tão-somente se, divide . q.e.d.
Em particular, notemos o valor da Função Totiente de Euler
Recordemo-nos de que a ordem de um elemento do grupo é o mínimo expoente tal que .
Teorema (Existência da raiz primitiva para um módulo que é a potência de ) Seja um inteiro positivo. Existe em tal que se, e tão-somente se, ou .
Demonstração: Se ou , então , e geram . Se , então, nenhum dos dois números ou tais que geram ; logo, não existe gerador. Se e , então . Logo, tampouco existe gerador. q.e.d.
Teorema (Existência da raiz primitiva para um módulo que é a potência de um número primo ímpar) Se é um número primo e um inteiro positivo, então existe em tal que
Demonstração: O caso já foi demonstrado. Mostremos primeiro o caso : Seja um gerador de e em . Temos isto é, para algum inteiro.
Se , então a ordem de . Como , pelo Teorema de Lagrange, a ordem de é ; isto é, gera .
Temos se, e tão-somente se, Como , se, e tão-somente se, Isto é, se , então gera .
Observemos que se então Logo, se a ordem de módulo é , então a ordem de módulo módulo é . Em particular, se gera , isto é, a sua ordem é em , então a ordem de é em , isto é, gera .
Por indução, o primeiro passo o caso já demonstrado acima, obtemos que se gera , então gera para todo . q.e.d.
Teorema Chinês dos Restos Sejam e inteiros. Se e tem nenhum divisor comum, então a aplicação natural dada por é bijetora.
Demonstração:
Se e , então, como e têm nenhum divisor comum, ; logo, a aplicação é injetora.
Seja em . Como e têm nenhum divisor comum, existem, pelo Algoritmo de Euclides Estendido, inteiros e tais que . Logo, satisfaz e . q.e.d.
Corolário. O grupo é cíclico, isto é, gerado por um único elemento, se, e tão-somente se,
Demonstração: Pelo Teorema Chinês dos Restos, se para primos , …, , então é bijetora e respeita , isto é, ; logo respeita , isto é, . Em particular, , e para todo em existe com se, e tão-somente se, existem , …, tais que , …, . Consequentemente é bijetora. Logo, como é ciclico para um primo , o produto é cíclico se, e tão-somente se, existe um único fator não-trivial.
O Pequeno Teorema de Fermat é uma observação útil quanto à ciclicidade da multiplicação nos anéis finitos para um número primo:
Como é finito (de cardinalidade ), para qualquer número diferente de , necessariamente terá uma repetição, para algum expoente e algum . Como em todo número exceto é invertível, podemos dividir por ; isto é, há tal que . Pelo Teorema de Lagrange, veremos que não somente , mas mais exatamente .
Este teorema nos servirá, por exemplo,
RSA.Observação. No entanto, não quer dizer que possivelmente já para . Com efeito, há muitos em para que isto vale: Para qualquer em e divisor de , a potência satisfaz já para . No mesmo tempo, acabamos de demonstrar que sempre há uma raiz primitiva, um gerador de ; isto é, necessariamente para todo .
Quanto à segurança criptográfica, o que pesa é o maior fator primo em ; por isso, os números primos queridos são da forma com primo, os primos seguros. Para facilitar os cálculos (sem perda de segurança),

Teorema. (Pequeno Teorema de Fermat) Se é um número primo, então, para qualquer número inteiro ,
Demonstração: Suponhamos que . Vale se, e tão-somente se, , e então em .
Suponhamos que . Como o grupo é finito, há e tais que . Como é primo, pelo Corolário 7.1. Em particular, podemos dividir por todo número exceto , em particular, por , e obtemos com . Pelo Teorema de Lagrange, , isto é, para um divisor . Logo .
Corolário. Se é um número primo, então, para qualquer número inteiro vale .
Com efeito, o Corolário equivale ao Pequeno Teorema de Fermat, porque se é primo, então pode se dividir por qualquer número (diferente de zero) em (diz-se que é um corpo).
Para demonstrar o Teorema de Lagrange, precisamos da noção de um grupo:
Definição. Um grupo é um conjunto com uma operação binária tal que
Teorema. (Lagrange) Seja um grupo. Se é um subgrupo de , então .
Demonstração: Define a relação sobre por se há em tal que . Como é um grupo, ela é transitiva e uma relação de equivalência. Logo é a união disjunta de classes de equivalência.
Seja em uma tal classe de equivalência . Por definição de , a aplicação é sobrejetora. Como é invertível (por ), ela é injetora, então uma bijeção.
Concluímos que todas as classes de equivalência têm cardinalidade e, pela união disjunta, que .
Recordemo-nos do Teorema de Euclides que asserta que haja números primos arbitrariamente grandes (por exemplo, com dígitos binários para o RSA):
Teorema de Euclides. Existe uma infinitude de números primos.
Demonstração: Suponhamos o contrário, que haja só um número finito de números primos. Considere Como é maior que , …, , não é primo. Seja então um número primo que divida . Pela hipótese, em . Mas por definição tem resto divido por qualquer , …, .
Contradição! Logo, não existe um maior número primo. q.e.d.
Marin Mersenne (Oizé, 1588 — Paris, 1648) foi um padre mínimo francês que tentou encontrar, sem êxito, uma fórmula para todos os números primos. Motivada por uma carta de Fermat em que lhe sugeriu que todos os números , os Números de Fermat fossem primos, Mersenne estudou os números Em 1644 publicou o trabalho Cogita physico-mathematica que afirma que estes são primos para (e erroneamente incluiu e ). Só um computador conseguiu mostrar em que é composto.
Os números primos de Mersenne, da forma para primo, conhecidos são
, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , e
O número primo tem algarismos. Foi encontrado no dia 8 de dezembro 2018 e é até hoje o maior número primo conhecido.
O CrypTool 1, na entrada do menu Indiv. Procedures -> Number Theory Interactive -> Compute Mersenne Numbers permite calcular uns números primos de Mersenne.
Um teste rápido se o número natural é composto é o Pequeno Teorema de Fermat (formulado pela sua contra-posição): Se há um número natural tal que então é composto.
Mas a implicação inversa, isto é, se é primo, então há um número natural tal que , não vale: Há números (que se chamam Números de Carmichael) que são compostos mas, para todo número natural , O menor tal número é (que é divisível por ).
O algoritmo mais simples para verificar se um número é primo ou não é o crivo de Eratóstenes (285 – 194 a.C.).

Para exemplificá-lo, vamos determinar os números primos entre e .
Inicialmente, determina-se o maior número pelo que dividiremos para verificar se o número é composto; é a raiz quadrada da cota superior arredondada para baixo. No caso, a raiz de , arredondada para baixo, é .
O próximo número da lista é primo. Repita o procedimento:
Conforme determinado inicialmente, é o último número pelo qual dividimos. A lista final contém só números primos.
Segue uma implementação em Python:
def primeSieve(sieveSize):
# Returns a list of prime numbers calculated using
# the Sieve of Eratosthenes algorithm.
sieve = [True] * sieveSize
sieve[0] = False # zero and one are not prime numbers
sieve[1] = False
# create the sieve
for i in range(2, int(math.sqrt(sieveSize)) + 1):
pointer = i * 2
while pointer < sieveSize:
sieve[pointer] = False
pointer += i
# compile the list of primes
primes = []
for i in range(sieveSize):
if sieve[i] == True:
primes.append(i)
return primesAKSO teste de AKS determina em tempo polinomial se é composto ou primo (mais exatamente, em tempo onde = o número de dígitos [binários] de ). Na prática, basta normalmente o Teste de Miller-Rabin probabilista que garante muito mais testemunhas (= números que provam se é composto ou não) do que o Pequeno Teorema de Fermat.
Com efeito, quando comparamos a duração entre os dois algoritmos para verificar se um número é primo num computador com um processador Intel Pentium-4 de 2 GHz, obtemos
| número primo | Miller-Rabin | AKS |
|---|---|---|
O CrypTool 1 oferece no Menu Individual Procedures -> RSA uma entrada para experimentar com diferentes algoritmos para detectar números primos.
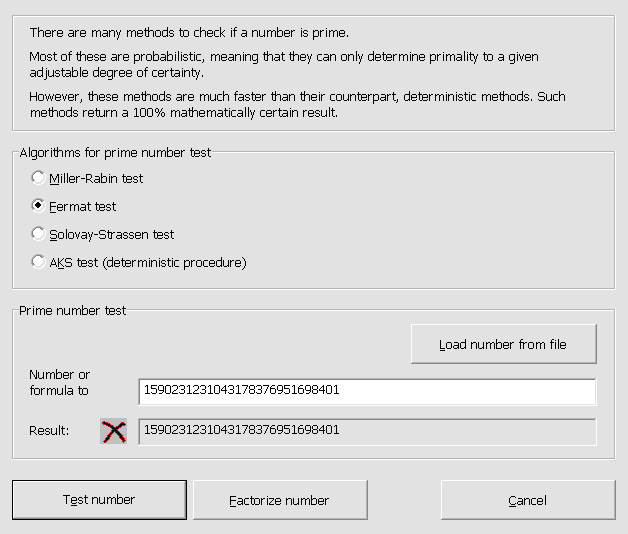
CrypTool 1Miller-RabinOs testes simplistas, para saber se um número é primo ou não, são ineficientes porque calculam os fatores de . Em vez deles, para saber apenas se é primo ou não, há o Teste de Miller-Rabin. Após a sua demonstração, damos a sua contraposição; é nesta formulação que é aplicado.
O Teste de Miller-Rabin. Seja um número primo, seja para números e (com ímpar). Então, para qualquer número inteiro indivisível por vale
Demonstração: Pelo Pequeno Teorema de Fermat Extraindo iterativamente a raiz quadrada, obtemos
Se para um número ímpar, um número possivelmente primo, escrevemos , então pelo Teste de Fermat não é primo se existe um inteiro tal que . O Teste de Miller-Rabin explicita a condição :
O Teste de Miller-Rabin. (Contraposição) Seja ímpar e para números e (com ímpar). Um inteiro relativamente primo a é uma Testemunha de Miller-Rabin (para a divisibilidade) de , se
Questão: Quais as chances que declaramos pelo Teste de Miller-Rabin acidentalmente um número primo, isto é, um número que é na verdade composto?
Teorema. (Sobre a frequência das testemunhas) Seja ímpar e composto. Então pelo menos dos números em são Testemunhas de Miller-Rabin para .
Logo, já depois de tentativas , , …, sem testemunha sabemos com uma chance , que o número é primo!
Vamos implementar
# Primality Testing with the Rabin-Miller Algorithm
# http://inventwithpython.com/hacking (BSD Licensed)
import random
def rabinMiller(num):
# Returns True if num is a prime number.
s = num - 1
t = 0
while s % 2 == 0:
# keep halving s while it is even (and use t
# to count how many times we halve s)
s = s // 2
t += 1
for trials in range(5): # try to falsify num's primality 5 times
a = random.randrange(2, num - 1)
v = pow(a, s, num)
if v != 1: # this test does not apply if v is 1.
i = 0
while v != (num - 1):
if i == t - 1:
return False
else:
i = i + 1
v = (v ** 2) % num
return Truedef isPrime(num):
# Return True if num is a prime number. This function does a
# quicker prime number check before calling rabinMiller().
if (num < 2):
return False # 0, 1, and negative numbers are not prime
# About 1/3 of the time we can quickly determine if num is not
# prime by dividing by the first few dozen prime numbers.
# This is quicker # than rabinMiller(), but unlike rabinMiller()
# is not guaranteed to prove that a number is prime.
lowPrimes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107,
109, 113, 127, 131, 137, 149, 151, 157, 163, 167, 173, 179, 181,
191, 193, 197, 199, 211, 223, 227, 233, 239, 241, 251, 257, 263,
269, 271, 277, 281, 283, 293, 307, 311, 313, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 431, 433,
439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509,
523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607,
613, 617, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691,
701, 709, 719, 727, 739, 743, 751, 757, 761, 769, 773, 787, 797,
809, 811, 821, 823, 827, 829, 853, 857, 859, 863, 877, 881, 883,
887, 907, 911, 919, 929, 937, 941, 947, 967, 971, 977, 983, 991,
997]
if num in lowPrimes:
return True
# See if any of the low prime numbers can divide num
for prime in lowPrimes:
if (num % prime == 0):
return False
# If all else fails, call rabinMiller() to check if num is a prime.
return rabinMiller(num)def generateLargePrime(keysize = 1024):
# Return a random prime number of keysize bits in size.
while True:
num = random.randrange(2**(keysize-1), 2**(keysize))
if isPrime(num):
return numApresentamos
RSA que se baseia na dificuldade de computar a fatoração em números primos, eDiffie-Hellman (para construir uma chave secreta mútua através de um canal inseguro),
ElGamal eECC, criptografia com curvas elípticasAmbos os algoritmos do tipo Diffie-Hellman, os algoritmosElGamal e ECC criam (em contraste ao RSA) uma chave efêmera para cada cifração e assinatura. É importante que esta chave seja imprevisível; caso contrário, esta informação permite a deduzir a chave privada. (Por exemplo, um aplicativo Bit Coin sob Android teve esta falha.)
Isto é, é preciso garantir que haja suficientemente entropia (isto é, desordem no sistema) na criação desta chave efêmera, usando como parâmetros particulares
RSAApresentamos o algoritmo RSA de Rivest, Shamir, e Adleman (1978) que cria
Em comparação ao protocolo de Diffie-Hellman, ele tem a vantagem que é completamente assimétrico:
não preciso de construir uma chave secreta mútua (e logo não expõe a chave secreto em dois lugares mas em um lugar só),
mas um único correspondente tem acesso à chave secreta. Contudo, neste caso a comunicação é cifrada só em direção do dono da chave secreta.
Para cifrar em ambas as direções,
RSA,As chaves para cifrar e decifrar serão construídas via a Fórmula de Euler que por seu turno se baseia no Pequeno Teorema de Fermat.
Pequeno Teorema de Fermat. Se é um número primo, então, para qualquer número inteiro ,
Em particular, para todo inteiro . Se , então
Isto é, se o expoente , então .
Em particular, se , isto é, e são tais que , em outras palavras, então isto é, Isto é, a computação da -ésima raiz iguala à da -ésima potência , um grande atalho computacional!
Exemplo. Por exemplo, para , e temos e . Por exemplo, para vale

Esta computação de por é o atalho do RSA. Porém, para ser secreto, precisamos dificultar a computação de a partir de . Dado e , o número tal que é diretamente calculado pelo algoritmo de Euclides.
No RSA, ao invés de um singelo primo , usamos um produto de dois números primos diferentes e que serão desconhecidos, cujo conhecimento é porém necessário (e dificílimo) para calcular ! Veremos primeiro como adaptar o Pequeno Teorema de Fermat, para um módulo ao módulo , a Fórmula de Euler:
Teorema. (Fórmula de Euler) Sejam e números primos diferentes. Se é divisível nem por , nem por , então
Demonstração: Pelo pequeno teorema de Fermat, e isto é, e dividem . Como e são primos diferentes, divide , isto é, .
Para números primos diferentes e , denote
Observação. Recordemo-nos de que a função totem de Euler de Seção 7.2 que conta o número de unidades em . Verifica-se que .
Pela Fórmula de Euler . Logo, como para o módulo em vez de ,
e geralmente:
Corolário. (Radiciação ) Sejam e números primos diferentes. Para qualquer expoente tal que vale
Demonstração: Como , isto é, há tal que , vale pela Fórmula de Euler,
Observação (crucial para o algoritmo RSA). Se , então pela Fórmula de Euler , isto é, a potenciação é a identidade, Em particular, se é o produto de dois números inteiros e , isto é, então Isto é, a potenciação inverte módulo , a extração da -ésima radiciação é a -ésima potência, Calcular uma potência é muitíssimo mais fácil do que uma raiz!
Exemplos.
Se e , então Se e , então .
Por exemplo, para a base , verificamos e Isto é,
Se e , então Se e , então .
Por exemplo, para a base , verificamos e Isto é,
Resumamos: Para números primos diferentes e , denote Se isto é, então
Recordemo-nos dos resultados de Seção 7.2:
Questão. Para quais existe tal que ?
Resposta: Para todo que é relativamente primo a , isto é, todo que tem nenhum divisor comum com .
Questão. Dado e que seja relativamente primo a , como calcular tal ?
Resposta: Pelo Algoritmo de Euclides.
(Recordemo-nos de que caracteres maiúsculos tendem a designar números públicos e caracteres minúsculos tendem a designar números secretos.)
Para a Alice enviar a mensagem secretamente ao Bob através de um canal inseguro,
Bob, para gerar a chave, escolhe
Bob, para transmitir a chave, envia à Alice
Alice, para cifrar,
Bob, para decifrar,
A computação de pela fatoração de é o atalho de que Bob dispõe.
O CrypTool 1 oferece no Menu Individual Procedures -> RSA Cryptosystem a entrada RSA Demonstration para experimentar com os valores das chaves e da mensagem no RSA.
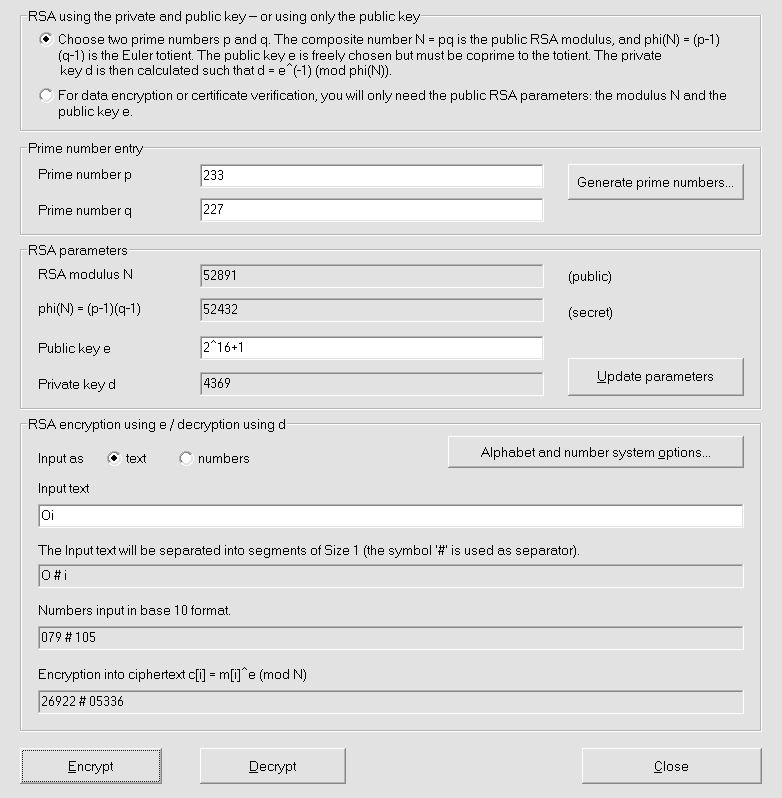
RSA no CrypTool 1Resumo. Observamos como
Como tudo se calcula pelo resto módulo (, um produto de dois primos e ), a radiciação é dificilimamente computável, não existem algoritmos muito mais rápidos do que o que prova todas as possibilidades e leva bilhões de anos.
Porém, pelo Teorema de Lagrange (ou, mais exatamente, a Fórmula de Euler), a radiciação de ordem é igual à potenciação para um número que o Algoritmo de Euclides calcula a partir de (e e , mais exatamente, de ). Logo, a chave secreta é , ou, suficientemente, o conhecimento dos fatores primos e de .
PythonVamos implementar o primeiro passo, a geração das chaves:
# RSA Key Generator
# http://inventwithpython.com/hacking (BSD Licensed)
import random, sys, os, rabinMiller, cryptomath
def main():
# create a public/private keypair with 1024 bit keys
print('Making key files...')
makeKeyFiles('al_sweigart', 1024)
print('Key files made.')
def generateKey(keySize):
# Creates a public/private key pair with keys that are keySize
# bits in size. This function may take a while to run.
# Step 1: Create two primes p and q. Calculate n = p * q.
print('Generating p prime...')
p = rabinMiller.generateLargePrime(keySize)
print('Generating q prime...')
q = rabinMiller.generateLargePrime(keySize)
n = p * q
# Step 2: Create a number e that is relatively prime to (p-1)*(q-1).
print('Generating e that is relatively prime to (p-1)*(q-1)...')
while True:
# Keep trying random numbers for e until one is valid.
e = random.randrange(2 ** (keySize - 1), 2 ** (keySize))
if cryptomath.gcd(e, (p - 1) * (q - 1)) == 1:
break
# Step 3: Calculate d, the mod inverse of e.
print('Calculating d that is mod inverse of e...')
d = cryptomath.ModInverse(e, (p - 1) * (q - 1))
publicKey = (n, e)
privateKey = (n, d)
print('Public key:', publicKey)
print('Private key:', privateKey)
return (publicKey, privateKey)
def makeKeyFiles(name, keySize):
# Creates two files 'x_pubkey.txt' and 'x_privkey.txt' (where x is
# the # value in name) with the the n, e and d, e integers written
# in them, delimited by a comma.
# safety check to prevent us from overwriting our old key files:
if os.path.exists('%s_pubkey.txt' % (name)) or
path.exists('%s_privkey.txt' % (name)):
sys.exit('WARNING: The file %s_pubkey.txt or %s_privkey.txt
# already exists! Use a different name or delete these files
# and re-run this program.' %(e, name))
publicKey, privateKey = generateKey(keySize)
print()
print('The public key is a %s and a %s digit number.' %
(str(publicKey[0])), len(str(publicKey[1]))))
print('Writing public key to file %s_pubkey.txt...' % (name))
fo = open('%s_pubkey.txt' % (name), 'w')
fo.write('%s,%s,%s' % (keySize, publicKey[0], publicKey[1]))
fo.close()
print()
print('The private key is a %s and a %s digit number.' %
(str(publicKey[0])), len(str(publicKey[1]))))
print('Writing private key to file %s_privkey.txt...' % (name))
fo = open('%s_privkey.txt' % (name), 'w')
fo.write('%s,%s,%s' % (keySize, privateKey[0], privateKey[1]))
fo.close()
# If makeRsaKeys.py is run (instead of imported as a module) call
# the main() function.
if __name__ == '__main__':
main()A implementação dos dois outros passos, a cifração e decifração:
# RSA Cipher
# http://inventwithpython.com/hacking (BSD Licensed)
import sys
# IMPORTANT: The block size MUST be less than or equal to the key size!
# (Note: The block size is in bytes, the key size is in bits. There
# are 8 bits in 1 byte.)
DEFAULT_BLOCK_SIZE = 128 # 128 bytes
BYTE_SIZE = 256 # One byte has 256 different values.
def main():
# Runs a test that encrypts a message to a file or decrypts a message
# from a file.
filename = 'encrypted_file.txt' # the file to write to/read from
mode = 'encrypt' # set to 'encrypt' or 'decrypt'
if mode == 'encrypt':
message = '''"Quem a raposa quer enganar, muito tem que madrugar" -RJ'''
pubKeyFilename = 'al_sweigart_pubkey.txt'
print('Encrypting and writing to %s...' % (filename))
encryptedText = encryptAndWriteToFile(filename, pubKeyFilename,
message)
print('Encrypted text:')
print(encryptedText)
elif mode == 'decrypt':
privKeyFilename = 'al_sweigart_privkey.txt'
print('Reading from %s and decrypting...' % (filename))
decryptedText = readFromFileAndDecrypt(filename, privKeyFilename)
print('Decrypted text:')
print(decryptedText)
def getBlocksFromText(message, blockSize = DEFAULT_BLOCK_SIZE):
# Converts a string message to a list of block integers.
# Each integer represents 128 (= blockSize) string characters.
messageBytes = message.encode('ascii') # convert string to bytes
blockInts = []
for blockStart in range(0, len(messageBytes), blockSize):
# Calculate the block integer for this block of text
blockInt = 0
for i in range(blockStart, min(blockStart + blockSize,
len(messageBytes))):
blockInt += messageBytes[i] * (BYTE_SIZE ** (i % blockSize))
blockInts.append(blockInt)
return blockInts
def getTextFromBlocks(blockInts, messageLength,
Size = DEFAULT_BLOCK_SIZE):
# Converts a list of block integers to the original message string.
# The original message length is needed to properly convert the
# last block integer.
message = []
for blockInt in blockInts:
blockMessage = []
for i in range(blockSize - 1, -1, -1):
if len(message) + i < messageLength:
# Decode the message string for the 128 (= blockSize)
# characters from this block integer.
asciiNumber = blockInt // (BYTE_SIZE ** i)
blockInt = blockInt % (BYTE_SIZE ** i)
blockMessage.insert(0, chr(asciiNumber))
message.extend(blockMessage)
return ''.join(message)
def encryptMessage(message, key, blockSize = DEFAULT_BLOCK_SIZE):
# Converts the message string into a list of block integers, and
# then encrypts each block integer. Pass the PUBLIC key to encrypt.
encryptedBlocks = []
n, e = key
for block in getBlocksFromText(message, blockSize):
# ciphertext = plaintext ^ e mod n
encryptedBlocks.append(pow(block, e, n))
return encryptedBlocks
def decryptMessage(encryptedBlocks, messageLength, key,
Size = DEFAULT_BLOCK_SIZE):
# Decrypts a list of encrypted block ints into the original message
# string. The original message length is required to properly decrypt
# the last block. Be sure to pass the PRIVATE key to decrypt.
decryptedBlocks = []
n, d = key
for block in encryptedBlocks:
# plaintext = ciphertext ^ d mod n
decryptedBlocks.append(pow(block, d, n))
return getTextFromBlocks(decryptedBlocks, messageLength, blockSize)
def readKeyFile(keyFilename):
# Given the filename of a file that contains a public or private key,
# return the key as a (n,e) or (n,d) tuple value.
fo = open(keyFilename)
content = fo.read()
fo.close()
keySize, n, EorD = content.split(',')
return (int(keySize), int(n), int(EorD))
def encryptAndWriteToFile(messageFilename, keyFilename, message,
Size = DEFAULT_BLOCK_SIZE):
# Using a key from a key file, encrypt the message and save it to a
# file. Returns the encrypted message string.
keySize, n, e = readKeyFile(keyFilename)
# Check that key size is greater than block size.
if keySize < blockSize * 8: # * 8 to convert bytes to bits
sys.exit('ERROR: Block size is %s bits and key size is %s bits.
RSA cipher requires the block size to be <= the key size!
Either increase the block size or use different keys.'
% (blockSize * 8, len(keySize))
# Encrypt the message
encryptedBlocks = encryptMessage(message, (n, e), blockSize)
# Convert the large int values to one string value.
for i in range(len(encryptedBlocks)):
encryptedBlocks[i] = str(encryptedBlocks[i])
encryptedContent = ','.join(encryptedBlocks)
# Write out the encrypted string to the output file.
encryptedContent = '%s_%s_%s' % (len(message), blockSize,
ptedContent)
fo = open(messageFilename, 'w')
fo.write(encryptedContent)
fo.close()
# Also return the encrypted string.
return encryptedContent
def readFromFileAndDecrypt(messageFilename, keyFilename):
# Using a key from a key file, read an encrypted message from a
# file and then decrypt it. Returns the decrypted message string.
keySize, n, d = readKeyFile(keyFilename)
# Read in message length and encrypted message from the file.
fo = open(messageFilename)
content = fo.read()
messageLength, blockSize, encryptedMessage = content.split('_')
messageLength = int(messageLength)
blockSize = int(blockSize)
# Check that key size is greater than block size.
if keySize < blockSize * 8: # * 8 to convert bytes to bits
sys.exit('ERROR: Block size is %s bits and key size is %s bits.
RSA cipher requires the block size to be <= key size!
Did you give the correct key file and encrypted file?'
% (blockSize * ySize))
# Convert the encrypted message into large int values.
encryptedBlocks = []
for block in encryptedMessage.split(','):
encryptedBlocks.append(int(block))
# Decrypt the large int values.
return decryptMessage(encryptedBlocks, messageLength, (n, d),
Size)
# If rsaCipher.py is run (instead of imported as a module) call
# the main() function.
if __name__ == '__main__':
main()Para assinar (em vez de cifrar), a única diferença é que os expoentes e trocam os seus papeis. Isto é, (em vez de ): Para a Samanta assinar a mensagem e o Vitor verificá-la,
Samanta, para gerar a rubrica (ou firma), escolhe
Samanta, para transmitir a rubrica, envia ao Vitor
Samanta, para assinar,
Vitor, para verificar,
Observação. A assinatura e a decifração são ambas a potenciação à chave privada . Logo, assinar um documento cifrado (pelo chave pública que corresponde a ) equivale a decifrá-lo! Por isso, na prática,
O CrypTool 1 oferece no Menu Individual Procedures -> RSA Cryptosystem a entrada Signature Generation para experimentar com os valores
Observamos que, em vez da mensagem original, é assinado
MD5) da mensagem original, e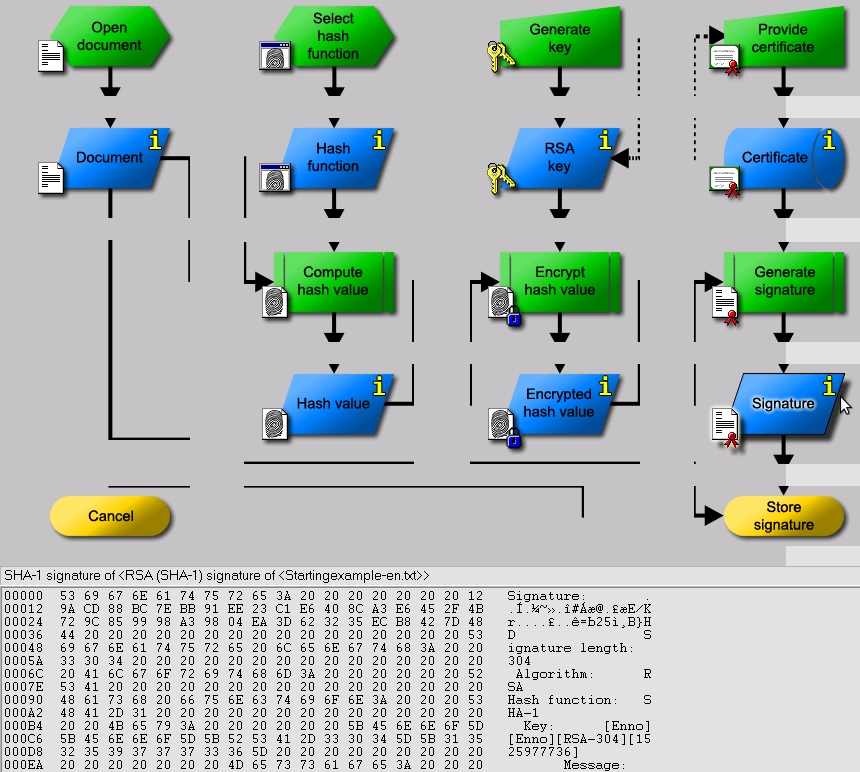
RSA no CrypTool 1Como são públicos
a segurança computacional de RSA baseia-se unicamente na dificuldade da computação da radiciação
O atalho é o conhecimento dos dois fatores primos e de que possibilita calcular
tal que, pela Fórmula de Euler, .
Um olheiro obteria a mensagem secreta a partir de , e , se pudesse computar isto é, a radiciação que inverte a potenciação ,
Enquanto a potenciação é facilmente computável, a radiciação é dificilmente computável para escolhas de e apropriadas, isto é, os números primos e suficientemente grandes (enquanto a escolha do expoente é arbitrário, por exemplo, popularmente ):
É o Teorema de Euclides que garante que haja números primos arbitrariamente grandes ( bits),
Atualmente, o algoritmo mais rápido para calcular a fatoração a partir de , é o campo de número de peneira geral de Lenstra et al. (1993). A grosso modo, o número de operações para fatorar um número inteiro de bits é
CPA = chosen plaintext attack)O atacante tem o texto cifrado e o texto claro correspondente, e pode escolher os textos claros; assim que o atacante possa deliberadamente variar, ou adaptar, o texto claro e analisar as alterações resultantes no texto cifrado. (A criptoanálise diferencial situa-se neste cenário.)
Este é o cenário mínimo para criptografia assimétrica! Como a chave de criptografia é pública, o atacante pode cifrar mensagens à vontade. Logo, se o atacante pode reduzir o número de textos claros possíveis, por exemplo, ele sabe que são ou “Sim” ou “Não”, então ele pode cifrar todos estes textos claros possíveis pela chave pública e compará-los com o texto cifrado interceptado. Para este o algoritmo modelar RSA não sofrer deste ataque, é preciso de preencher o texto claro por dados aleatórios para robustecê-lo contra este ataque CPA.
Na prática, a mensagem secreta precisa de ser enchida, isto é, aleatoriamente aumentada. Senão, quando a mensagem clara e o expoente são pequenos (por exemplo, ), possivelmente a mensagem cifrada satisfaz . Neste caso, a igualdade Por isso, é facilmente computável, por exemplo,
Um ataque hipotético mais simples é o de Wiener quando a chave privada é pequena: Observação. O Teorema de Wiener se aplica quando , isto é, é pequeno demais, e , isto é, e são próximos demais.
Seja com e números primos diferentes; põe . Seja a chave pública e , isto é, .
Tem-se , se, e tão-somente se, existe tal que se, e tão-somente se, Dividindo por ,
Teorema (de Wiener). Se , então é uma fração contínua que aproxima .
Se as condições do teorema são satisfeitas, então, como é público, é possível achar o segredo como denominador da fração contínua (mais exatamente, de uma convergente de uma fração contínua) aproximativa .
Observação. O Teorema de Wiener se aplica quando , isto é, é pequeno demais, e , isto é, e são próximos demais.
Demonstração: Por definição , se existe um inteiro com . Logo e . Usemos como aproximação a , visto que e logo (pois ).
Logo
Como , vale . Logo
O número das frações para que estão tão próximas de é limitado por , e todas tais frações são frações contínuas de . Isto é, o atacante apenas tem de calcular as primeiras frações contínuas de , e uma delas será (que é irredutível porque implica que ).
Concluímos então que um algoritmo em tempo linear basta para encontrar a chave secreta .
Afim de implementar o ataque de Wiener, segue o código Python para
calcular as frações contínuas que se aproximam da fração :
calcular a fração a partir de uma fração contínua com coeficientes :
Observação. Mencionamos que se ao contrário (e não ) é muito pequeno, então um ataque é muito mais difícil; vide o artigo retrospetivo por Boneh nas Notices of the AMS.
ElGamalApresentamos o algoritmo ElGamal que cria
Em particular, permite aos dois correspondentes de comunicar cifradamente através de um canal inseguro como na troca de chaves de Diffie-Hellman (se cada correspondente cria a sua própria chave pública e privada e compartilha a chave pública).
Este algoritmo, tão próximo da troca de chaves de Diffie-Hellman, cria uma chave secreta mútua. Isto é, como na troca de chaves de Diffie-Hellman, falta a vantagem (da criptografia assimétrica em comparação à criptografia simétrica) que a chave é comprometível em um único lugar.
Contudo, esta desvantagem é teórica, porque para cada mensagem uma nova chave mútua é criada. Se um atacante tem acesso à chave do remetente, provavelmente também à mensagem que enviou.

Em contraste ao RSA, onde os correspondentes precisam,
os algoritmos que se baseiam no protocolo de Diffie-Hellman, que estabelece apenas uma chave secreta mútua e precisa da interação dos correspondentes, isto é, ambos tem de ser online, precisam, para contornar esta disponibilidade,
Para a Alice enviar a mensagem secretamente ao Bob através de um canal inseguro, combinam primeiro
onde apropriado se refere às mesmas propriedades como para o algoritmo de Diffie-Hellman, isto é,
Veja https://asecuritysite.com/encryption/elgamal para uma demonstração dos passos em JavaScript.
Observação. Em vez da multiplicação de por , qualquer outra operação invertível é possível; por exemplo, a adição .
ElGamalVeremos que e facílimo verificar mas dificílimo calcular a solução de uma equação módulo um número primo grande que foi potenciada de ambos os lados por uma base : para resolvê-la precisaria
Na assinatura,
É isto uma assinatura, um vínculo infalsificável entre um documento e uma identidade.
Protocolo: Para a Samanta assinar um documento e o Vitor verificar a assinatura, combinam primeiro
onde apropriado se refere às mesmas propriedades como para o algoritmo de Diffie-Hellman, isto é,
Observação. Para calcular a partir de , e , usa-se a fórmula , isto é, precisa de calcular o logaritmo modular que leva tempo exponencial. É preciso saber e para calcular em tempo polinomial. Isto explica porque em vez de aparece como expoente de : caso contrário, Samanta teria de publicar com ; isto revelaria a sua rubrica secreta !
Advertência. Se um dos dois números secretos, ou ou , for conhecido, então ambos, e , serão conhecidos (pela fórmula )! Em particular, se a chave secreta auxiliar (efêmera) for conhecida, então a rubrica secreta (permanente) será conhecida pela fórmula ! Por exemplo, se é usada para cifrar dois documentos diferentes e , então há tantas (isto é, duas) equações quanto incógnitas ( e ); logo, ambas podem ser resolvidas, isto é, e obtidas! Logo, é importantíssimo usar uma única vez e manter secreta; em particular, a sua geração tem de ser suficientemente aleatória.
DSAA assinatura DSA baseia-se na assinatura do ElGamal (para um módulo primo com dígitos binários), mas é computacionalmente seis vezes mais econômica porque trabalha com um grupo menor de potências de (de cardinalidade com dígitos binários para um fator primo de ao invés da cardinalidade com dígitos binários).
Protocolo: Para a Samanta assinar um documento e o Vitor verificar a assinatura, combinam primeiro
Os dados públicos são , e
SHA-1 do documento .Observamos, que em comparação com o El Gamal, o algoritmo DSA
Como explica a subsecção Módulos Arbitrários em Seção 6.2, esta diminuição da ordem da base compromete a segurança moderadamente:
Se o módulo é produto de dois fatores e sem fator comum, então o logaritmo modular pode ser computado, pelo Teorema Chinês dos Restos, a partir dos logaritmos pelo Algoritmo de Euclides (estendido).
Se o módulo é uma potência de um primo , então o logaritmo modular módulo pode ser computado em tempo polinomial a partir do logaritmo módulo
Entre todas as curvas, a graça das elípticas (dadas por uma equação ) é que permitem somar pontos ( se uma reta passa por e ). Ao restringirmos da equação às soluções em para um grande número primo e fixarmos um tal ponto ,
A criptografia por curvas elípticas ECC (Elliptic Curve Criptography) é uma variação do protocolo de Diffie-Hellman:
A vantagem de usar como problema criptográfico,
é que em dependência do número de bites de (pelos algoritmos mais rápidos presentemente conhecidos)
Por exemplo, a segurança obtida por uma chave de bites para o logaritmo multiplicativo equivale aproximadamente à de uma chave de bites para o logaritmo sobre uma curva elíptica.
Nas próximas secções:
Anteriormente nos damos conta que já usamos a aritmética modular no dia-a-dia, por exemplo, para o módulo , na aritmética do relógio, e para , nos dias da semana. Mais geralmente, definimos, para um número inteiro qualquer, o anel finito (= um conjunto finito em que podemos somar e multiplicar); a grosso modo definimo-lo
Se é primo, então mostramos em Seção 5.2 que é um corpo denotado por . Isto é, para todo em exceto , sempre existe em , o inverso multiplicativo de definido por . Em outras palavras, em um corpo podemos dividir por qualquer número exceto . (Os exemplos mais comuns são os corpos infinitos , e .)
Na criptografia, curvas elípticas são definidas sobre corpos cuja cardinalidade é uma potência de um número primo (e não somente da forma como era o caso até agora); por exemplo, para um número grande.
O caso é particularmente apto para a computação (criptográfica). Os corpos da forma são chamados binários. Demos primeiro um nome ao número que figura em .
Definição: O número primo é a característica do corpo, o menor em tal que .
O corpo para é definido por polinômios de grau sobre ,
Rijndael Corpo Por exemplo, para com e , obtemos o corpo usado no AES. Como conjunto isto é, as somas finitas para , , …, em .
Seja para primo e em . Como conjunto, isto é, as somas finitas para , , …, em .
AES).Uma curva sobre um corpo (de característica ) é elíptica se dada por uma equação para coeficientes e tais que a curva não seja singular, isto é, que a sua discriminante não se esvaía, .
Nota.
A equação é a forma de Weierstraß, mas existem várias outras que se revelaram computacionalmente mais eficientes, como a de Montgomery que pode ser transformada em uma equação de Weierstrass pela substituição
Se a característica é , isto é, com , a equação tem a forma .
Após escolha de um domínio (por exemplo, , , , ou para um número primo ) os pontos que resolvem esta equação formam uma curva no plano sobre ele. Além dos pontos no plano, existe também o ponto no infinito (ou ponto ideal) que é denotado . Resumimos que, como conjunto, a curva elíptica é dada por Sobre um corpo finito , o número dos pontos é limitado por onde , isto é, assimptoticamente igual à cardinalidade . (O algoritmo de Schoof computa em cerca de operações para o número de dígitos binários de .)
Para o domínio , as curvas assumem as seguintes formas no plano real para diferentes parâmetros e :
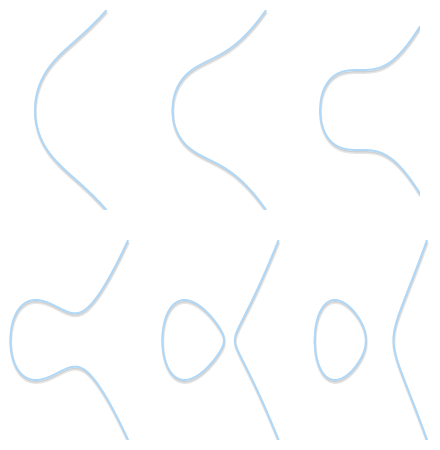
Enquanto sobre os corpos finitos, obtemos um conjunto discreto de pontos (simétrico em volta do eixo horizontal médio).
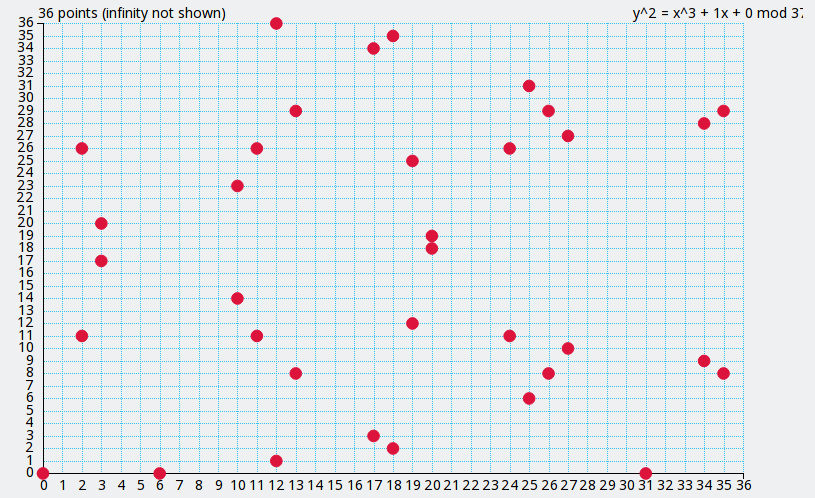
Para o algoritmo criptográfico sobre esta curva ser seguro, isto é, a computação do logaritmo sobre ela demorar, existem restrições nas escolhas de e da curva elíptica (isto é, dos seus coeficientes definidores e ), por exemplo,
RSA com chaves de bits),A probabilidade que uma curva aleatoriamente gerada (isto é, cujos coeficientes e na equação sejam gerados aleatoriamente) seja vulnerável a um destes ataques é negligenciável.
Escolhas seguras são, entre outras:
Curve25519 com sobre com onde (de onde o seu nome); o seu número de pontos é . (Esta curva tornou-se popular como alternativa imparcial às curvas recomendadas, e logo desconfiadas, pelo NIST o “National Institute for Standards and Technology”.)nistk163, nistk283, nistk571 e nistb163, nistb283, nistb571 definidas sobre o corpo binário com , e bites.Brainpool P256r usada para cifrar os dados no micro-chip da carteira de identidade alemã.SHA-1.Os pontos de uma curva elíptica podem ser somados. Como é esta soma definida? Geometricamente a soma de três pontos , e numa curva elíptica no plano euclidiano (isto é, em ) é definida pela igualdade se uma reta passa por e . Contudo, sobre corpos finitos esta igualdade geometria não se aplica mais e precisamos de uma definição algébrica (e a qual é além disto a única maneira que o computador entende).
Com efeito, os pontos da curva elíptica com a adição formam um grupo comutativo. Um grupo comutativo é um conjunto com
uma adição, isto é, uma operação binária que, dados dois argumentos e , produz um resultado denotado por e a qual é
e para a qual
Exemplos.
Dada uma curva elíptica, ela define um grupo
Se olhamos os pontos reais da curva , isto é, todos os pontos em tais que , então a adição tem uma significação geométrica: Tem-se se , e estão na mesma reta. Isto é,
O espelhamento de ao longo do eixo- é o ponto .
O CrypTool 1 demonstra esta adição geométrica em uma animação acessível na entrada Point Addition on Elliptic Curves no menu Indiv. Procedures -> Number Theory - Interactive.
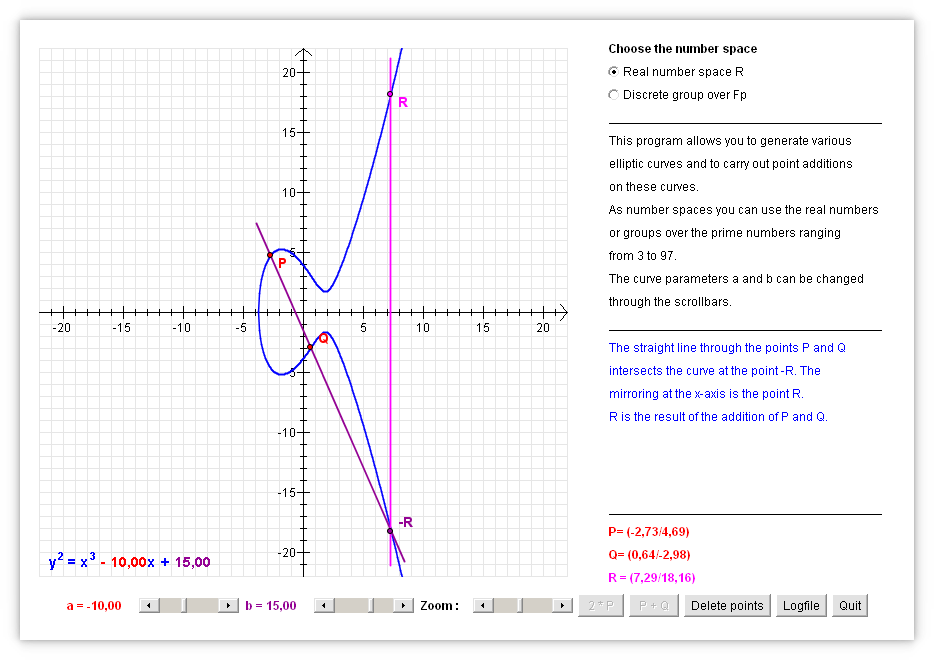
CrypTool 1Esta descrição geométrica da adição nos leva à seguinte descrição algébrica: Expressa por coordenadas cartesianas a adição de dois pontos de uma curva elíptica é dada por uma fórmula algébrica, isto é, envolve apenas as operações básicas da adição, multiplicação e potenciação. (Logo, podemos substituir as incógnitas por valores em qualquer domínio, seja , , ou .)
Proposição: Denote Se a curve é dada por e os pontos , e são não-nulos, então onde é o grau da inclinação da reta que passa por e , dada por
Demonstração: Dada a curva sobre o corpo (cuja característica seja ), e os pontos = (, ) e = (, ) na curva.
Se , então seja a equação cartesiana da linha que intersecta e com a inclinação
Para os valores , e a equação da linha é igual à da curva ou, equivalentemente, As raízes dessa equação são exatamente , e ; logo
Logo, o coeficiente de dá o valor ; o valor de segue por substituir na equação cartesiana da linha. Concluímos que as coordenadas (, ) = = -( + ) são
Se = , então
Observação. Para certas curvas específicas, estas fórmulas podem ser simplificadas: Por exemplo, numa Curva de Edwards da forma para (com elemento neutro o ponto ), a soma dos pontos e é dada pela fórmula (e o inverso de um ponto é ). Se não é um quadrado em , então não existem pontos excecionais: Os denominadores e são sempre diferentes de zero.
Se, em vez de , olhamos os pontos com entradas em um corpo finito da curva , isto é, todos os pontos em tais que , a adição é univocamente definida pela fórmula .
O CrypTool 1 demonstra esta adição na entrada Point Addition on Elliptic Curves no menu Indiv. Procedures -> Number Theory - Interactive.
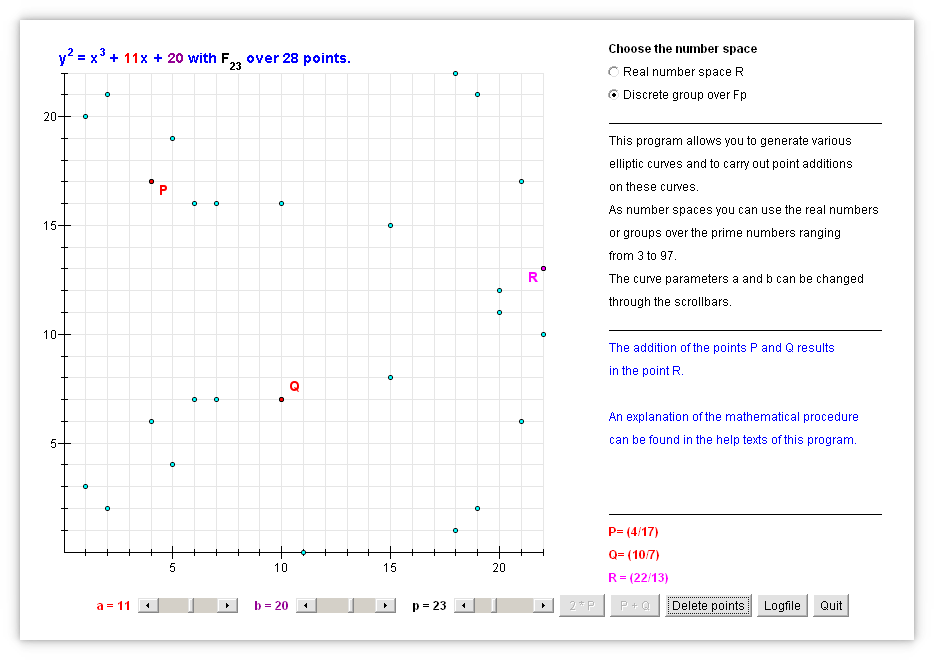
CrypTool 1A adição leva à multiplicação escalar pela iterada adição. Isto é,
Como o grupo de pontos sobre um corpo finito é finito (de cardinalidade aproximativamente ), necessariamente para qualquer ponto o conjunto é finito. Isto é, existem e em tais que , isto é, existe um inteiro tal que .
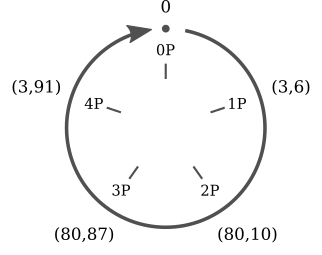
Nota. O site http://www.graui.de/code/elliptic2/ mostra para uma curva elíptica sobre um corpo finito da forma a tabela de adição entre os pontos, e para cada ponto o grupo finito gerado por ele.
A cardinalidade é o menor tal que e é chamada de ordem do ponto . Pelo Teorema de Lagrange (em Seção 7.2), divide .
Para cifrar, além
é escolhido
O número criptograficamente mais importante é a ordem do ponto de base , que, para resistir
Para encontrar um ponto de base de uma ordem suficientemente grande e com a ordem do corpo suficiente grande (para resistir contra o Pollard’s attack), executa os passos seguintes:
Proposição. O ponto assim encontrado tem ordem .
Demonstração: Para qualquer ponto , vale pelo Teorema de Lagrange. Isto é, para , e pelo Teorema de Lagrange divide . Como é primo, ou , ou . Como , vale , isto é, .
Exemplos (de pontos de base).
A curva elíptica Curve25519 com sobre com onde , usa como ponto de base univocamente determinado
(Uns pontos com tem uma ordem consideravelmente menor que a de .)
A curva elíptica secp256k1 definida pela equação sobre com = em notação hexadecimal (especificada pelo SECG, o “Standards for Efficient Cryptography Group”, implementada por OpenSSL, e, entre outros, usada pelo Bitcoin para assinar transações) usa como ponto de base com
ECCA criptografia por curvas elípticas ECC (Elliptic Curve Criptography) usa a troca de Chaves de Diffie-Hellman para
A cifração pela ECC é padronizada pelo ECIES (Elliptic Curve Integrated Encryption Scheme), um procedimento híbrido (mistura criptografia assimétrica com criptografia simétrica).
Uma vez a chave (= um ponto da curva elíptica finita) secreta mútua estabelecida, Alice e Bob derivam dela uma chave para uma cifra simétrica como AES ou 3DES. (Esta derivação chama se uma KDF (Key Derivation Function) função de derivação de chave que transforma uma informação secreta no formato apropriado. Uma tal função padronizada é a ANSI-X9.63-KDF com a opção SHA-1.) Por exemplo, o protocolo TLS
Transferimos o protocolo de Diffie-Hellman da multiplicação em um corpo finito à adição em uma curva elíptica finita: Denote um ponto da curva, e a iterada adição ( vezes) sobre a curva elíptica finita (em vez de e para o grupo multiplicativo de um corpo finito).
No protocolo ECDH (Elliptic Curve Diffie-Hellman), para Alice e Bob construírem uma chave secreta através de um canal inseguro, combinam primeiro
e depois
isto é, é importante que é um grupo.
O protocolo ECDHE, com o E adicional significando ‘Ephemeral’, é quanto à troca de chaves igual ao protocolo ECDH. ‘Ephemeral’ significa que as chaves são efémeras (e necessariamente assinadas pelas chaves permanentes).
PythonEm https://github.com/andreacorbellini/ecc/blob/master/scripts/ecdhe.py encontra-se uma implementação em Python do ECDH.
Elliptic Curve Digital Signature Algorithm é uma modificação do algoritmo DSA que usa a iterada adição de dois pontos de uma curva elíptica no lugar da exponenciação de dois números usada pelo DSA. A principal vantagem deste algoritmo é que ele pode se contentar com chaves menores para oferecer a mesma segurança que DSA o RSA devido aos ataques (conhecidos) menos avançados.
ECDSAPara a Samanta assinar um documento e o Vitor verificar a assinatura, combinam primeiro
Observação. Observamos, que em comparação com o DSA, o algoritmo ECDSA
Advertência. Se um dos dois números secretos, ou , ou , for conhecido, então ambos, e , serão conhecidos (pela fórmula )! Em particular, se a chave secreta auxiliar (efêmera) for conhecida, então a rubrica secreta (permanente) será conhecida pela fórmula ! Logo, é importantíssimo que guardar secreta; em particular, a sua geração tem de ser suficientemente aleatória.
PythonEm https://github.com/andreacorbellini/ecc/blob/master/scripts/ecdsa.py encontra-se uma implementação em Python do ECDSA.
A ECC, a criptografia por curvas elípticas finitas ganha mais e mais popularidade porque o seu problema criptográfico (o logaritmo sobre uma curva elíptica finita) é presentemente considerado computacionalmente mais difícil do que o do RSA (a fatoração em primos) ou do ElGamal (o logaritmo sobre o grupo multiplicativo de um corpo finito). Por isso, chaves pequenas para a ECC conseguem o mesmo nível de segurança como chaves grandes para o RSA ou o ElGamal. Como exemplo, a segurança obtida por uma chave de bites da ECC corresponde à obtida por uma chave de bites do RSA ou ElGamal. Esta economia entre os tamanhos das chaves de um fator considerável corresponde a uma economia computacional de um fator semelhante. Quanto a usabilidade,
ECC pode ser compartilhada por soletração (são letras na notação hexadecimal,RSA ou ElGamal tem que ser compartilhada por um arquivo (a que é referida por uma impressão digital por conveniência).Estudamos o problema criptográfico por trás da ECC em mais detalhes e comparamo-lo com o do RSA e El Gamal.
Ambos os grupos considerados na criptografia, o grupo multiplicativo de um corpo finito e o grupo de uma curva elíptica finita, são grupos cíclicos finitos, isto é, gerados por um elemento de ordem finita . Matematicamente dito, são iguais a um grupo do tipo
Dado um gerador em , a identificação de com por , a exponencial é rapidamente computado em qualquer grupo comutativo : Dado em , para calcular , expande na base binária para , …, em e calcula por multiplicação por sucessivamente , , …, . Então Isto é, calculamos em operações do grupo.
Exemplo. Para o grupo de pontos de uma curva elíptica, em , e em calculamos sucessivamente , , . Sejam , , … os índices dos dígitos binários , , … que são diferentes de . Então
Porém, dado um gerador em , a computação da identificação inversa, do logaritmo isto é, dado em , calcular em tal que é geralmente árdua: Pelo Teorema de Shoup em Shoup (1997), todo algoritmo genérico, isto é, que usa apenas as operações do grupo, leva pelo menos operações (do grupo) para calcular o logaritmo.
Um algoritmo genérico que atinge esta rapidez (exceto um fator ) é o Baby Step, Giant Step (ou algoritmo de Shanks): Dado h em , para calcular em tal que :
Este algoritmo funciona, pois:
Nota. Para curvas elípticas, o Pollard’s -algorithm é levemente mais rápido.
Esta estimativa das operações necessárias para computar o logaritmo de um grupo, isto é, que usa apenas as operações do grupo, aplica-se a algoritmos genéricos. Contudo, algoritmos específicos, isto é, que usam as propriedades específicos do grupo (como o das unidades de um corpo finito ou o de uma curva elíptica), podem usar menos.
Por exemplo, para o grupo multiplicativo de um corpo finito, existem, com efeito, algoritmos mais rápidos (chamados sub-exponenciais) para calcular a fatoração e o logaritmo. São baseados no Index Calculus que faz uso das propriedades deste grupo específico. Por exemplo, para os problemas criptográficos do RSA e Diffie-Hellman sobre o grupo multiplicativo de um corpo finito, isto é,
o algoritmo presentemente mais rápido é o Campo de número de peneira geral (de Lenstra et al. (1993) para a fatoração, e de Gordon (1993) para o logaritmo).
A grosso modo, a sua complexidade, o número de operações do grupo, (dita sub-exponencial) para um grande é onde e significa uma função sobre tal que para .
Em contraste, todos os algoritmos conhecidos para o problema criptográfico da ECC, isto é, calcular o logaritmo sobre uma curva elíptica finita, são algoritmos genéricos. Para estes algoritmos genéricos, pelo Teorema de Shoup, a complexidade no número de bites da entrada é a menor possível. O algoritmo presentemente mais rápido é o Pollard’s -algorithm que tem a grosso modo uma complexidade (dita exponencial) de onde .
Esta Tabela compara os tamanhos de chaves em bites a um nível de segurança comparável entre
AES,Diffie-Hellman ou o RSA.| Chave Simétrica | Chave Assimétrica Elíptica | Chave Assimétrica Clássica |
|---|---|---|
| 80 | 160 | 1024 |
| 112 | 224 | 2048 |
| 128 | 256 | 3072 |
| 192 | 384 | 7680 |
| 256 | 512 | 15360 |
Os números da tabela são estimados pelo algoritmo, presentemente, mais rápido para resolver os seus problemas criptográficos: Dada uma chave de entrada de bites,
AES, o algoritmo mais rápido é provar todas as possíveis chaves, cuja complexidade (= o número de operações) é RSA, ou Diffie-Hellman, sobre o grupo multiplicativo de um corpo finito, o algoritmo mais rápido é o Campo de número de peneira geral (baseado no Index Calculus) cuja complexidade, a grosso modo, para um grande é Na prática, estas chaves menores da ECC aceleram por um fator as operações criptográficas em comparação às do RSA e ElGamal (além de facilitarem a sua troca entre homens e economizam largura de banda). Contudo, recordemo-nos que existem também desvantagens da ECC em comparação ao RSA:
Pseudo Random Number Generator, um gerador de números aleatórios que, quando é mal programado, revela a chave privada!ECC é mais recente; por isso:
RSA, eCerticom).Uma função (hash ou de dispersão ou de espalhamento) é um algoritmo que envia
isto é, mapeia uma sequência de baites de um comprimento arbitrariamente grande para uma sequência de baites de comprimento fixo, usualmente entre e bites; conceptualmente, transforma uma grande quantidade de dados em uma pequena quantidade de informações.
Para ser uma função hash razoável, precisa de
A função de hash é criptográfica (ou uma função de embaralhamento) se o algoritmo resiste
Segundo o princípio de Kerckhof, o algoritmo deve ser público.
Na prática, a resistência
MD4, MD5 e SHA-1 que não resistem contra colisões, mas continuam a ser populares.Por exemplo, o algoritmo CRC é uma função de hash (não criptográfica); funções de hash criptográficas comuns são, por exemplo, MD4, MD5, SHA-1, SHA-256 e SHA-3.
O valor de uma função hash é chamado de hash ou checksum (= soma de verificação) ou dispersão ou escrutínio. Frequentemente, tem um comprimento de ou baites e é representada em base hexadecimal cujos algarismos são de a e de A a F.
Por exemplo, o valor da função hash SHA-256 da entrada Oi! é
e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855Lembremo-nos de que uma função hash razoável é
Logo, se, por exemplo, a saída tem bites, então idealmente cada valor deveria ter a mesma probabilidade . Isto é, a saída identifica a entrada praticamente univocamente (com uma chance de colisão de idealmente ); Por isso, convém pensar de um hash de dados, por exemplo, de um arquivo, como a sua (carteira de) identidade (ou mais exatamente, o número da identidade, ou CPF, já que o hash é um número); um hash identifica muitos dados por pouca informação.

Como o comprimento a sequência do hash é limitada (raramente bites) enquanto o comprimento a sequência da entrada é ilimitada, existem colisões, isto é, hashes iguais de arquivos diferentes. Porém, o algoritmo minimiza a probabilidade de colisões pela distribuição mais uniforme possível dos seus valores: Intuitivamente, torná-los o mais aleatórios possíveis; mais exatamente, toda sequência de comprimento fixo possível é um valor e a probabilidade de cada um dos valores é a mesma.
Os algoritmos de hash (criptográficos) mais usados são os de baites ( bites) MD4 e MD5 ou o SHA-1, de baites ( bites). Apesar de todos eles, MD4, MD5 e SHA-1 não resistem contra colisões, continuam populares para usos sem alto risco.
MD4 (Message-Digest algorithm): Desenvolvido em 1991 por Ron Rivest, um dos três criadores do algoritmo RSA e (da empresa RSA Data Security); rápido, mas vulnerável a criação de pré-imagens. Descrito na RFC 1320.
MD5: Desenvolvido pela RSA Data Security. Descrito na RFC 132. Enquanto é vulnerável a colisões, mas não à criação de uma segunda imagem inversa. Muito utilizado para
P2P, ou Peer-to-Peer, em inglês), eSHA-1 (Secure Hash Algorithm): Desenvolvido pelo NIST, o National Institute for Standards and Technology. É vulnerável a colisões, mas não à criação de uma segunda imagem inversa.
WHIRLPOOL: função criptográfica de hash desenvolvida por Paulo S. L. M. Barreto e por Vincent Rijmen, o co-autor do AES; relativamente recente, e até hoje, em 2018, considerada segura. Foi adotada como parte do padrão internacional ISO 10118-3.
Atualmente recomendáveis são, entre outros, as versões mais recentes SHA-256 e SHA-3 do Secure Hash Algorithm.
Damos exemplos de funções hash ruins, isto é,
Para a construção de funções hash (criptográficas) atuais como MD4 olha, por exemplo, a Tese de Diploma por Daniel Knopf. O embaralhamento é conseguido por iterações
semelhante às cifras de bloco como o AES.
Divisão com resto (ou congruência linear) por um número (natural) ,
Por exemplo, para e obtemos pois .
Quando , a divisão com resto é o truncamento da expansão binária de à sua soma incial até a -ésima entrada; por exemplo, para
Soma dos dígitos (binários), isto é,
As duas funções podem ser compostas, isto é,
Por exemplo, quando é uma potência de , o truncamento da soma dos dígitos binários a certo número de dígitos binários.
O meta-método de Merkle, ou a construção Merkle-Damgård, constrói a partir de uma função de compressão sem perda (isto é, cujas entradas têm o mesmo comprimento como a saída) uma função de compressão com perda, isto é, uma função de hash. Ele permite reduzir à imunidade da função hash inteira contra
à correspondente imunidade da função de compressão.
Esta construção precisa de
IV = initialization value),Com são calculados para Isto é, na computação do hash do bloco atual entra, além do valor do bloco atual, o valor da função de compressão do último bloco.
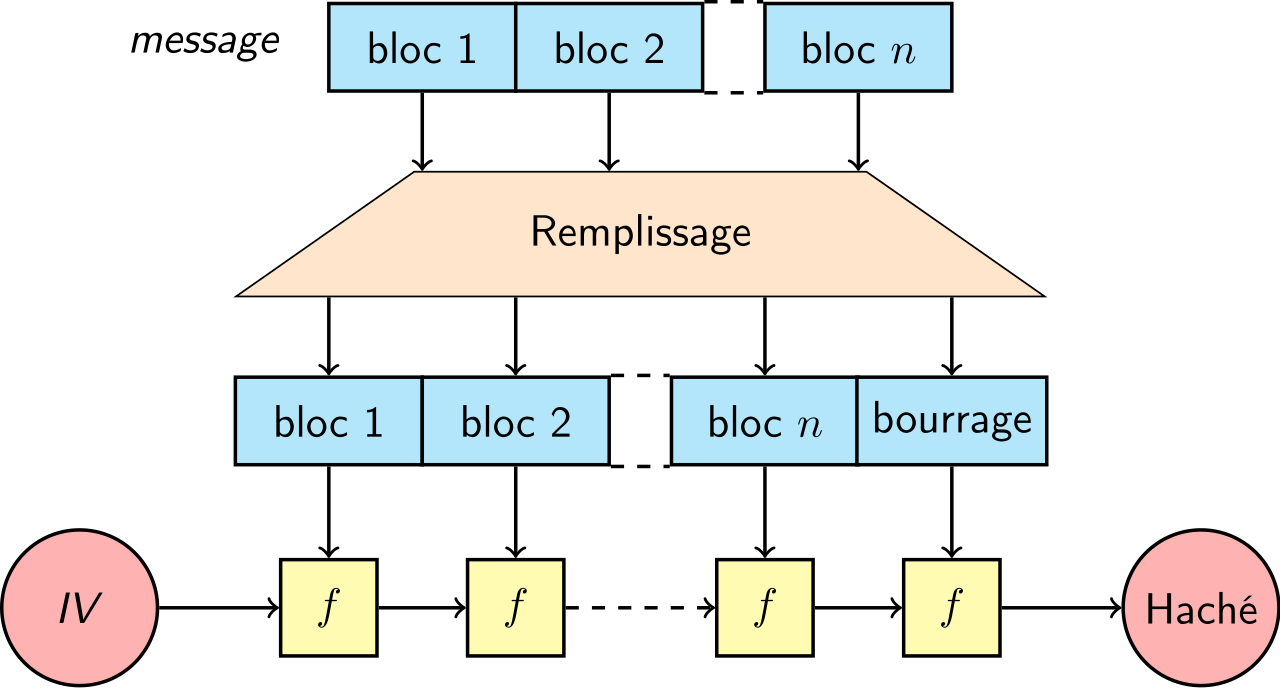
A função de compressão consiste de uma Cifra de Feistel (ou rede de substituição e permutação) onde
XOR) a . Isto é XOR) a . Isto é A adição de garante que a função de compressão não seja mais invertível (ao contrário da cifra para uma chave fixa); isto é, para dada saída, não é mais possível saber a entrada (única). Caso contrário, para criar uma colisão, dada uma saída , poderia decifrar por chaves diferentes, e para obter entradas diferentes e .
Para reduzir a imunidade da função hash à da de compressão, o acolchoamento precisa satisfazer as condições suficientes:
O acolchoamento mais simples que cumpre estas condições é a que anexa o comprimento a e enche o segmento entre o fim de e pelo número de s prescrito pelo tamanho do bloco, isto é, a concatenação
Para evitar colisões, não basta o acolchoamento encher o resto da mensagem com zeros: Desta maneira, duas mensagens que só diferem no número de zeros finais no último final teriam o mesmo acolchoamento!
Em vez disto, a maneira mais simples seria anexar um dígito , e em seguida o resto com s. Porém, veremos que isto permitiria colisões com o meta-método de Merkle se o valor inicial IV foi escolhido da seguinte maneira:
Denotem os blocos da mensagem e o valor inicial. O hash é calculado pela iterada aplicação da função de compressão A graça do meta-método de Merkle é a redução de colisões da função hash à função de compressão: uma colisão do hash implicaria uma colisão da função de compressão, isto é, diferentes pares de blocos e com .
Para ver isto, observamos que
Sem o comprimento no acolchoamento, a colisão de duas mensagens com comprimentos diferentes só pode ultimamente ser reduzida a uma pré-imagem do valor inicial sob a função de compressão, isto é, um valor tal que
Se a sua escolha foi arbitrária, os autores de MD5 e SHA-256 poderiam ter inserida a seguinte porta traseira: Ambos os algoritmos usam o esquema de Mayer-Davis, isto é, uma função de compressão para uma cifra de Feistel com chave ; em particular, com fixo, a função de decifração é invertível! Ora, se quisessem, os autores poderiam ter escolhido uma chave e ter definido exatamente tal que . Logo , isto é, uma colisão entre os hashes de e !
Já que, por exemplo, MD5 e SHA-256 escolhem como um valor cuja pré-imagem supostamente não é conhecida (por exemplo, os dígitos hexadecimais em ordem crescente no MD5 ou os dígitos decimais dos primeiros oito primos no SHA-256) este problema é sobretudo teórico antes de prático.
SHA-256Pseudo-Código do SHA-1
Note 1: All variables are unsigned 32-bit quantities, and
wrap modulo 232 when calculating, except for
- ml, the message length, which is a 64-bit quantity, and
- hh, the message digest, which is a 160-bit quantity.
Note 2: All constants in this pseudo code are in big endian.
Within each word, the most significant byte is stored leftmost.
Initialize variables:
h0 = 0x67452301
h1 = 0xEFCDAB89
h2 = 0x98BADCFE
h3 = 0x10325476
h4 = 0xC3D2E1F0
ml = message length in bits
(always a multiple of the number of bits in a character).
Pre-processing:
append the bit '1' to the message, e.g.
by adding 0x80 if message length is a multiple of 8 bits.
append 0 <= k < 512 bits '0', such that the resulting message length
in bits is congruent to -64 \equiv 448 (mod 512)
append ml, the original message length, as a 64-bit big-endian integer.
Thus, the total length is a multiple of 512 bits.
Process the message in successive 512-bit chunks:
break message into 512-bit chunks
for each chunk
break chunk into sixteen 32-bit big-endian words w[i], 0 <= i <= 15
Extend the sixteen 32-bit words into eighty 32-bit words:
for i from 16 to 79
w[i] = (w[i-3] xor w[i-8] xor w[i-14] xor w[i-16]) leftrotate 1
Initialize hash value for this chunk:
a = h0
b = h1
c = h2
d = h3
e = h4
Main loop:[3][55]
for i from 0 to 79
if 0 \leq i \leq 19 then
f = (b and c) or ((not b) and d)
k = 0x5A827999
else if 20 \leq i \leq 39
f = b xor c xor d
k = 0x6ED9EBA1
else if 40 \leq i \leq 59
f = (b and c) or (b and d) or (c and d)
k = 0x8F1BBCDC
else if 60 \leq i \leq 79
f = b xor c xor d
k = 0xCA62C1D6
temp = (a leftrotate 5) + f + e + k + w[i]
e = d
d = c
c = b leftrotate 30
b = a
a = temp
Add this chunk's hash to result so far:
h0 = h0 + a
h1 = h1 + b
h2 = h2 + c
h3 = h3 + d
h4 = h4 + e
Produce the final hash value (big-endian) as a 160-bit number:
hh =
(h0 leftshift 128) or (h1 leftshift 96) or
(h2 leftshift 64) or (h3 leftshift 32) or h4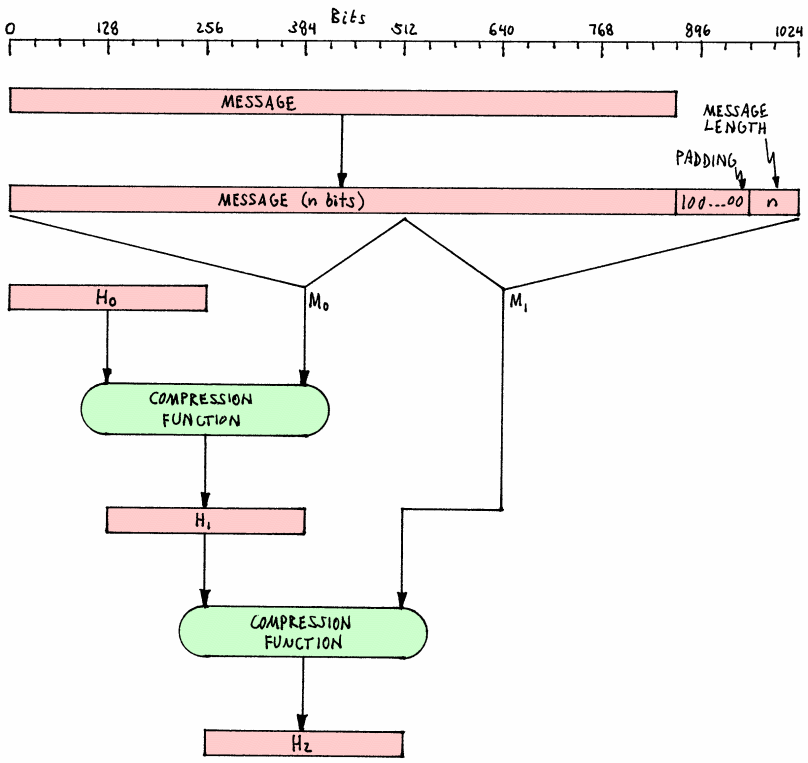
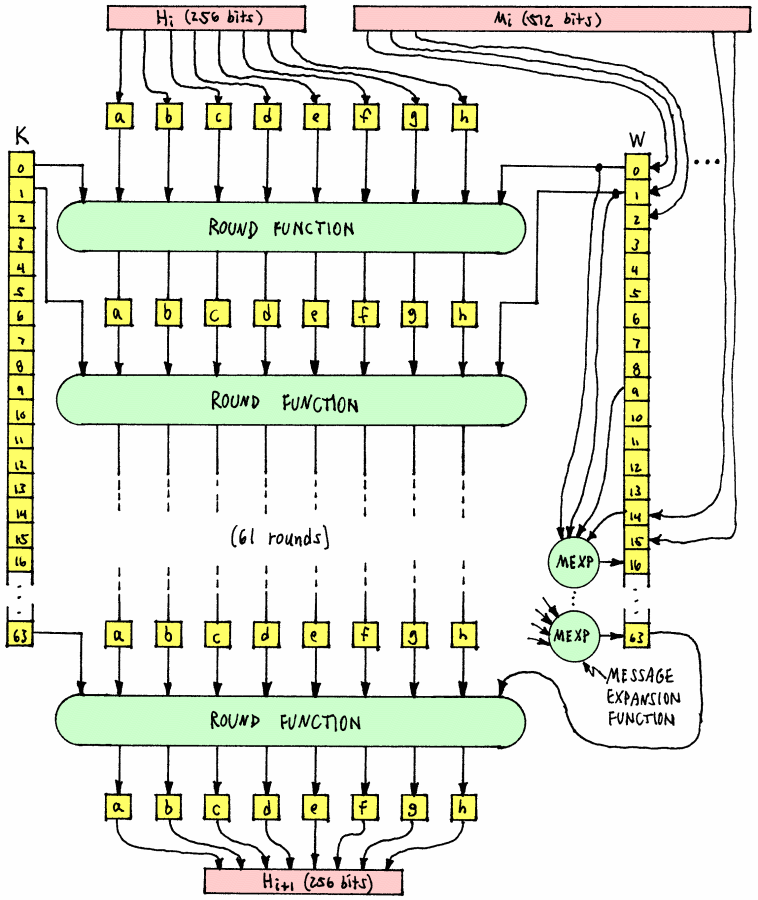
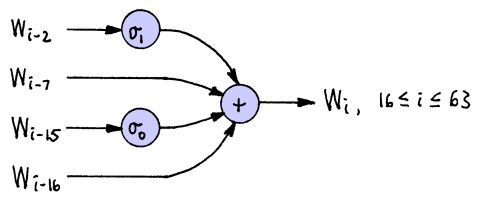
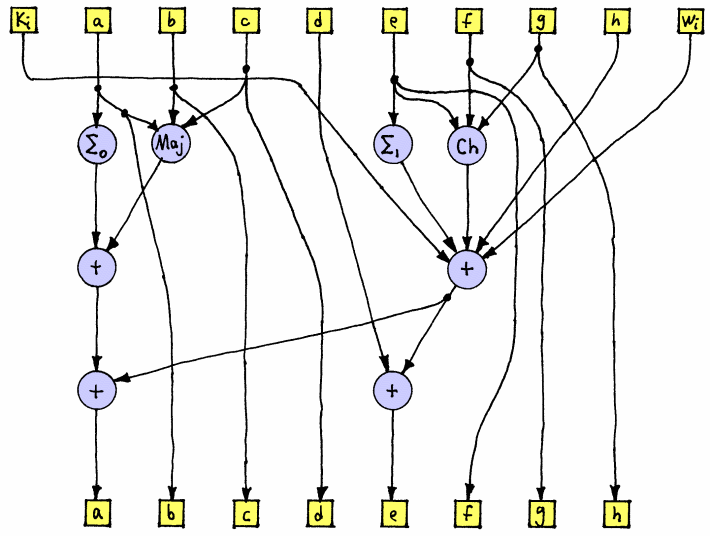
onde as funções nos diagramas são definidas pelas operações básicas:
Em http://www.metamorphosite.com/one-way-hash-encryption-sha1-data-software tem uma explicação detalhada e um simulador do SHA-1.
Funções de Hash (não necessariamente criptográficas, como CRC) são usadas:
para consulta de dados rápidas (isto é, em tempo fixo, independente do número de entradas)
para garantir a integridade de um arquivo diante modificações acidentais, isto é, para detetar diferenças entre o arquivo e uma versão de referência (tipicamente a antes do transporte do arquivo).
Funções de Hash criptográficas são usadas:
key stretching), intuitivamente, torná-los menos previsíveis; isto é, como KDF (= Key Derivation Function);
PBKDF (= Password Based Key Derivation Function).Observação: Atenção à diferença entre autenticidade e autenticação: A primeira garante a igualdade dos dados recebidos e enviados de uma pessoa (por exemplo, na assinatura digital), a última a identidade desta pessoa (por exemplo, no acesso de um site seguro).
Os algoritmos de hash criptográficos alistados acima, MD4/5, SHA … distribuem os valores uniformemente, mas são rápidos; logo, não são apropriados à criação de senhas, porque são vulneráveis a ataques de força bruta. Para impedi-los, é necessário que o algoritmo do PBKDF, por exemplo, PBKDF1, PBKDF2, bcrypt, scrypt, Argon2 (um candidato novo e o mais prometedor), seja
GPU, um microprocessador gráfico, eASIC, um microprocessador, ou Circuito Integrado, Adaptado para uma aplicação eSpecífica, aqui a computação de um hash;bcrypt; escrypt);salt, uma pitada de sal, um argumento adicional único, comumente aleatório [e gerado por outra função de hash], da função de hash): sem salt, o algoritmo é propenso a ataques por Rainbow Tables, a comparação com os hashes das entradas mais prováveis (guardados em tabelas, donde o nome do ataque), por exemplo, das senhas mais usuais.Uma tabela hash (ou tabela de dispersão) usa uma função hash para endereçar as entradas (= linhas) de um array, isto é, uma tabela de dados.
Cada entrada tem um nome, isto é, uma identificação única (= chave). Por exemplo, a chave é o nome de uma pessoa. Os dados da chave, por exemplo, o seu número de telefone, são guardados em uma linha da tabela. Estas linhas são numeradas a partir de .

O número da linha, o seu endereço, da chave é determinado pelo seu hash. Como vantagem, em tempo fixo, os dados podem
Enquanto,
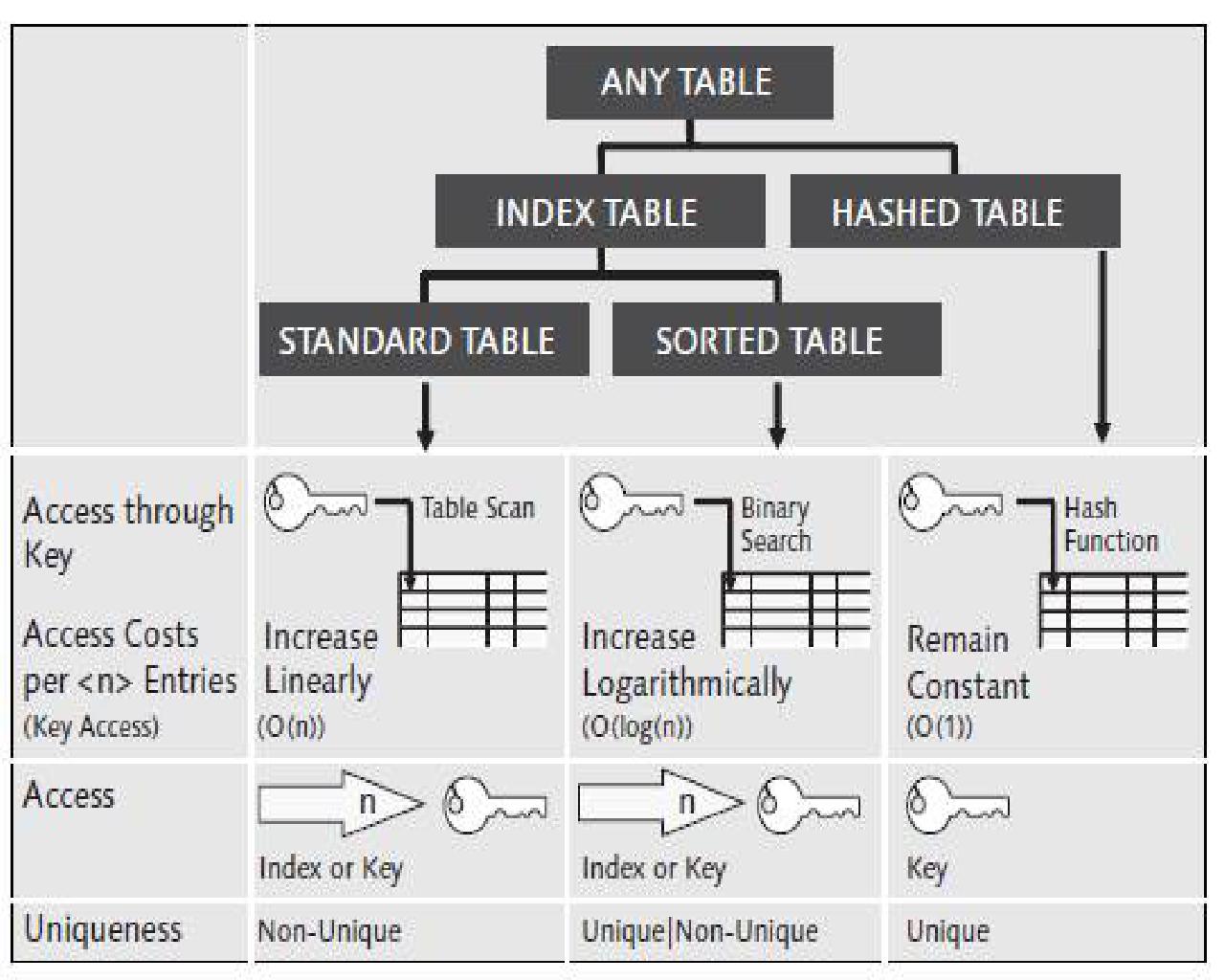
Colisões, isto é, duas entradas com o mesmo hash são mais frequentes do que se imagina; vide o Paradoxo do Aniversário. Para evitar colisões, é necessário
Quando ocorrem colisões, umas estratégia são
em vez do número de hash endereçar uma única entrada, usar Chaining: endereçar um bucket, um balde de várias entradas, uma lista, ou
usar Open Hashing: colocar a entrada em outra posição livre, por exemplo,
Double Hashing).Até da tabela sendo repletos, ocorrem em média colisões. Isto é, encontrar uma entrada leva operações. Para comparar, com entradas, levaria em média
Porém, depois deste fator as colisões ocorrem com uma tal frequência que o uso de outra estrutura de dados, por exemplo, uma árvore binária, é recomendável.
Uma árvore de dispersão ou de Merkle (inventada em 1979 por Ralph Merkle) agrupa dados em blocos por uma árvore (binária), cujos vértices (= nós) são hashes e cujas folhas (= nós terminais) contêm os blocos de dados, para poder verificar rapidamente (em tempo linear) cada bloco de dados pela computação do hash da raiz.
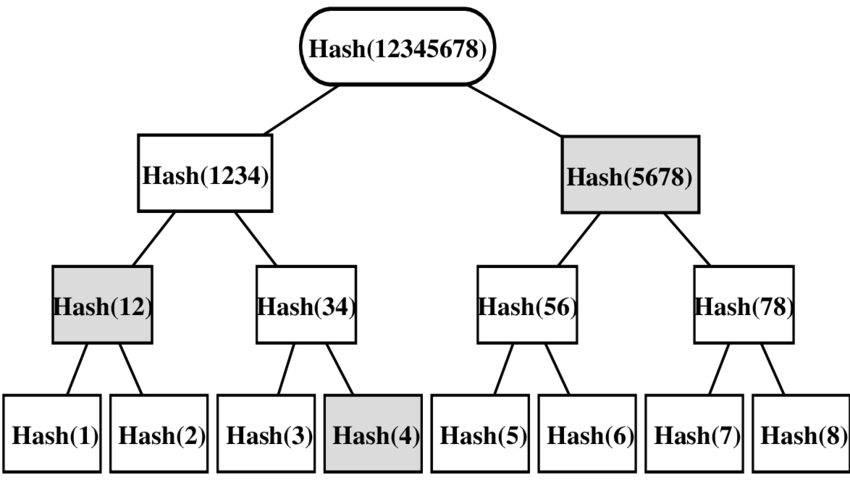
Em uma árvore de dispersão de profundeza (= folhas )o bloco de dados de cada folha é verificável
O principal uso de árvores de Merkle é garantir que blocos de dados recebidos de outros pares em uma rede ponto-a-ponto (P2P) sejam recebidos intactos e inalterados.
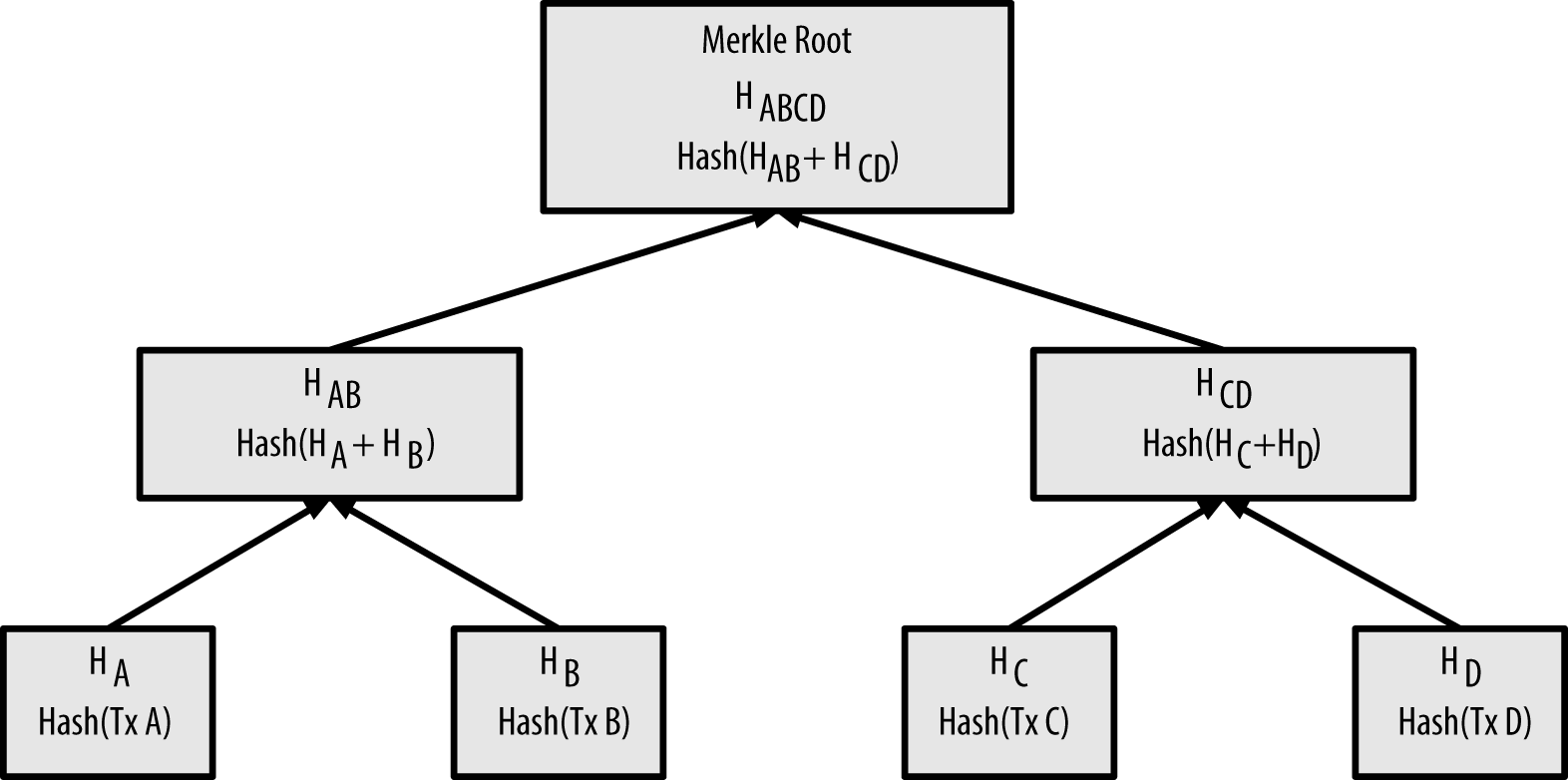
Uma árvore de Merkle é uma árvore (usualmente binária) de hashes cujas folhas são blocos de dados de um arquivo (ou conjunto de arquivos). Cada nó acima das folhas na árvore é o hash dos seus dois filhos. Por exemplo, na imagem,
Hash(34) é o hash da concatenação dos hashes Hash(3) e Hash(4), isto é, ,Hash(1234) é o hash da concatenação dos hashes Hash(12) e Hash(34), isto é, , eHash(12345678) é o hash da concatenação dos hashes Hash(1234) e Hash(5678), isto é, .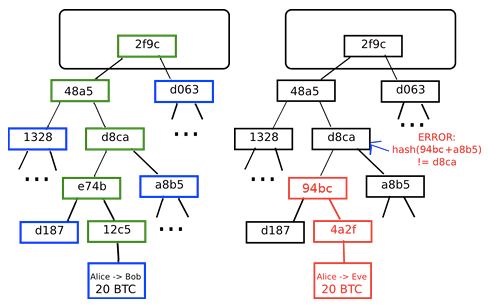
Normalmente uma função de embaralhamento *criptográfico* é usada, por exemplo, SHA-1. Porém, se a árvore de Merkle só precisa proteger contra danos involuntários, somas de verificação não necessariamente criptográficas, como CRCs são usadas.
No topo da árvore de Merkle reside a dispersão de raiz ou dispersão mestre. Por exemplo, em uma rede P2P, a dispersão de raiz é recebida de uma fonte confiável, por exemplo, de um site reconhecido. A árvore de Merkle em si é recebida de qualquer ponto na rede P2P (não particularmente confiável). Esta árvore de Merkle (não particularmente confiável) recebida é comparada pelo cálculo dos hashes das folhas com a dispersão de raiz confiável para verificar a integridade da árvore de Merkle.
A principal vantagem de uma árvore (de profundeza com folhas, isto é, blocos de dados), em vez de uma lista, de dispersão é que a integridade de cada folha pode ser verificada pelo cálculo de (em vez de ) hashes (e a sua comparação com o hash da raiz).
Por exemplo, em Figura 10.1, a verificação da integridade da Folha requer apenas
Hash(4) Hash(12), e Hash(5678), eHash(3) Hash(34), Hash(1234), e Hash(12345678)Hash(12345678) calculado e o hash obtido da fonte confiável.Ao contrário de uma moeda comum, em que os negociantes confiam em um terceiro, o banco, que mantém um livro-razão de todas as transações, em uma criptomoeda, eles confiam em uma blockchain, literalmente cadeia de blocos, um livro-razão público de todas as transações; mantido (e replicado) por uma rede de milhares de computadores e praticamente infalsificável.
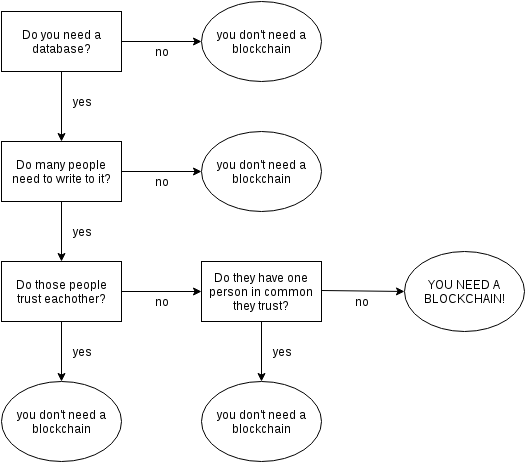
Para poder confiar na cadeia de blocos (na ausência de um terceiro), isto é, para garantir a imutabilidade dos blocos antigos (= os que já figuram na cadeia em contraste aos que serão acrescentados), a cadeia tem de ser pública, isto é, toda a rede pode ler e acrescentar blocos. Com efeito, é perfeitamente viável alterar (blocos antigos d’) a cadeia; porém, esta alteração será detetada pela rede e em seguida a cadeia alterada rejeitada.
Os meios criptográficos para implementar uma criptomoeda são
Recordemo-nos de que uma função hash é uma função que envia (praticamente sempre) sequências de bites diferentes (de um comprimento arbitrariamente grande) a sequências de bites diferentes (de um comprimento fixo). Os seus valores, os hashes, servem como informações curtas que endereçam, ou indicam, (praticamente sem equívoco) dados grandes, por exemplo,
A função de hash é criptográfica, se o processo é praticamente unidirecional, isto é, se o Hash não permite fazer conclusões sobre o conteúdo original. O Bitcoin usa esta dificuldade da computação da entrada de uma saída de uma função de hash “como prova de trabalho” que é necessário para estender a blockchain, o livro-razão, impedindo a sua alteração (maléfica).
Existem outras criptomoedas, cada uma com as suas próprias características. Destacam-se, entre outras, por exemplo,
BurstCoin que usa uma “prova de espaço” em vez de uma prova de trabalho, isto é, a reserva de um espaço no disco rígido, para ganhar moedas.Tem também a inconveniência que todas as transações do Bitcoin são públicas (com como única ofuscação o conhecimento da pessoa por trás da chave pública [por trás do endereço Bitcoin]). Para aumentar a privacidade, existem, entre outras moedas
Monero que usa assinaturas de grupo (vide Seção 4.1) para confirmar as transações entre os negociantes, assim ofuscando o fluxo das moedas, eZcash que usa zk-SNARKs em vez de assinaturas de grupo, uma prova de não-interativa conhecimento zero.Veremos
Sobrevoemos a arquitetura da Blockchain (do Bitcoin):
A blockchain, literalmente, é uma cadeia de blocos. Há um bloco inicial, o bloco Genesis e blocos que apontam aos seus antecessores.
Esta flecha que aponta ao antecessor é um hash, uma identificação do conteúdo inteiro do bloco antecedente; é um endereço que figura no cabeçalho do bloco.
O tronco do bloco consiste de transações, em média 2000 delas, entre os usuários do bitcoin.
Como o hash do bloco depende do conteúdo inteiro do bloco, a singela alteração de um bit muda o seu hash, isto é, invalida a flecha do sucessor para ele! Logo, para os blocos continuarem a formar uma cadeia, é preciso alterar esta flecha. Logo, o hash do sucessor muda! Logo, para os blocos continuarem a formar uma cadeia, é preciso alterar a flecha do sucessor do sucessor, e assim por diante, uma reação em cadeia!
Quer dizer, se alterarmos algum detalhe, por exemplo, uma transação no primeiro bloco, todas as flechas (= hashes) que seguem têm de ser recalculadas!
Entra a questão da mineração que dificulta muito esta alteração, porque somente blocos cujos hashes são pequenos, quer dizer começam com muitos zeros, são aceitos pela rede (isto é, pelos nós que verificam). Então, não basta alterar uma transação e calcular os novos hashes de todos os sucessores. É preciso fazer esta alteração tal que todos os hashes sejam pequenos!
É muito difícil encontrar uma tal alteração. Atualmente, a busca de um tal bloco requer um bilhão de anos num computador usual; mas só dez minutos pela rede dos mineradores. Enquanto o malfazejo começou a buscar os blocos aceitáveis, a rede já criou vários outros, invalidando este trabalho!
Todos os bitcoins que existem foram gerados por mineração, isto é, foram dados (pela coinbase transação) como recompensa àquele que criou um bloco (com um hash pequeno).
Todas as outras transações têm uma entrada e saída. Na entrada junta-se uma quantia suficiente para pagar o que será gastado. Tem de gastar tudo! Por isso, usualmente uma transação inclui o remetente como destinatário, o troco. O que não for gastado ganhará o minerador que incluirá esta transação no seu bloco como recompensa (atualmente em volta de 40 $).
O destinatário é designado pela sua chave pública, e só na hora em que gastará as moedas precisa de demonstrar a posse da sua chave privada correspondente, pela sua assinatura da transação.
O Bitcoin usa a criptografia com curvas elípticas finitas para assinar as transações. O Diffie-Hellman usa anéis finitos como (por exemplo, para o relógio, e um número primo como com 100 algarismos no Bitcoin). O conceito usado pelo Bitcoin semelha à de Diffie-Hellman, só que em vez números usa pares de números , isto é, pontos de uma curva, de um gráfico, dito elíptica.
A graça desta curva é que podemos adicionar pontos: vale se os três pontos estão na mesma reta. Em vez de multiplicar várias vezes o mesmo número, adicionamos o mesmo ponto. É fácil adicionar pontos com esta receita sobre estes anéis finitos, mas é dificílimo saber quantas vezes um ponto foi adicionado a si mesmo para obter o ponto resultante. A cifração corresponde à adição, a decifração ao conhecimento deste número de vezes.
Finalmente, o esquema de assinatura é uma variação da assinatura de ElGamal: a assinatura demonstra que o dono da chave privada conseguiu resolver uma equação difícil, tão dificílimo que é praticamente impossível resolvê-la sem esta chave privada que fornece um atalho.
A blockchain é uma cadeia de blocos que são ligados, isto é, cada bloco tem um hash de outro bloco, de que pensamos como um indicador (ou endereço) para o bloco anterior.
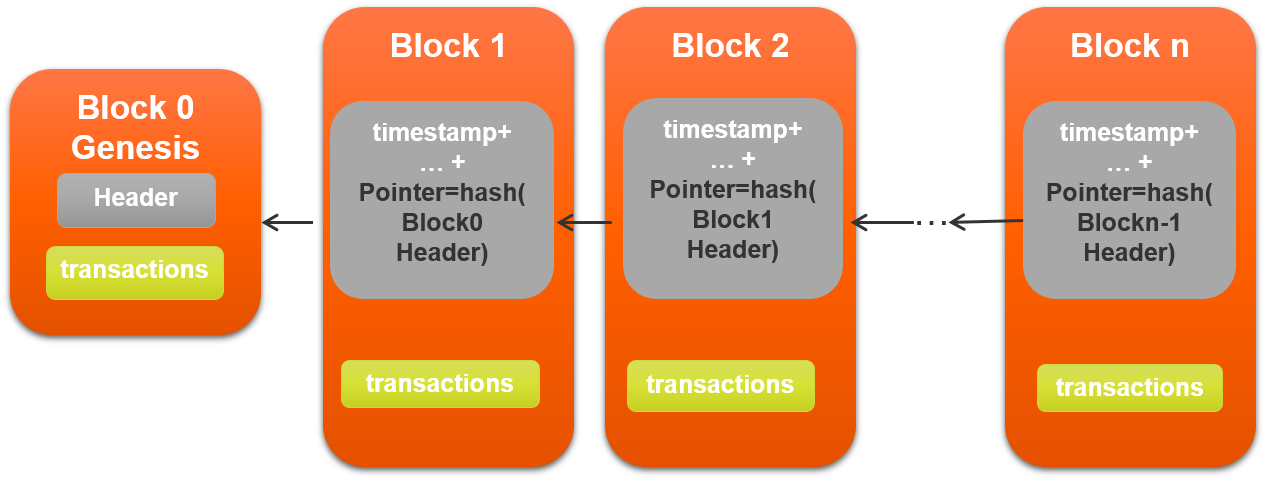
Ocorrem ramificações, blocos orfanados; porém, só a cadeia mais comprida (mais exatamente, esta cuja construção era computacionalmente a mais trabalhosa, isto é, a soma das dificuldades dos trabalhos dos blocos; vide prova de trabalho em Seção 11.4) é considerada válida. Como é dificílimo estender a cadeia por outro bloco, raramente as ramificações têm mais de um bloco.
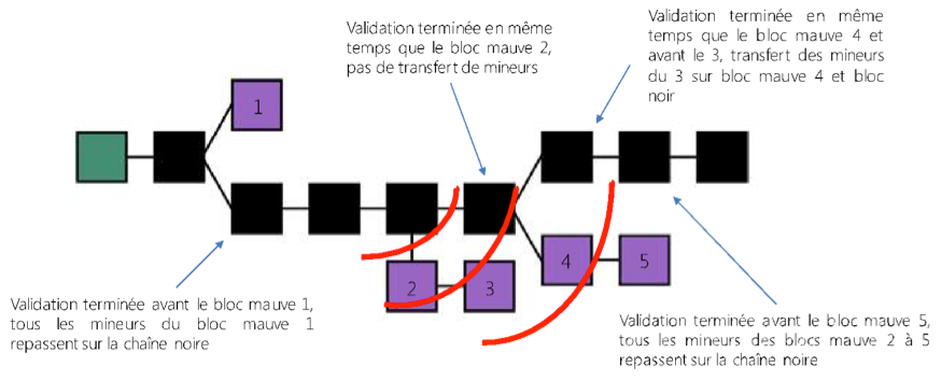
A cadeia começou no dia 3 em janeiro de 2009 às 18:15 UTC, provavelmente por Satoshi Nakamoto, com o primeiro bloco, o bloco de Génesis.
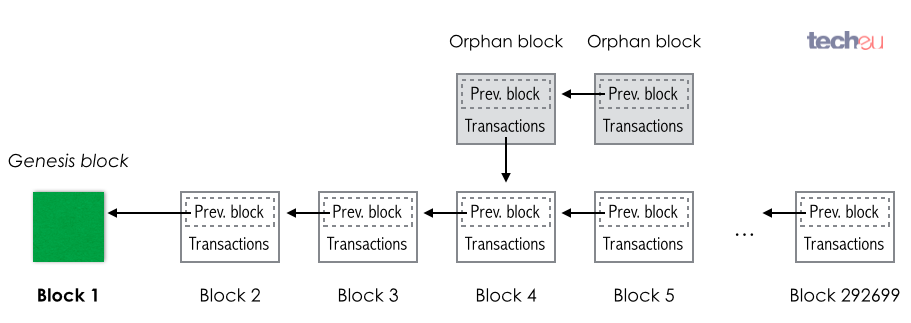
Cada bloco consiste
O hash do bloco depende do seu conteúdo todo. Isto é, qualquer alteração, implica a alteração do seu hash, em particular,
Por exemplo:
Em outras palavras, ocorre uma reação em cadeia: A alteração de uma singela transação em um bloco invalida todos os hashes dos seus blocos posteriores.
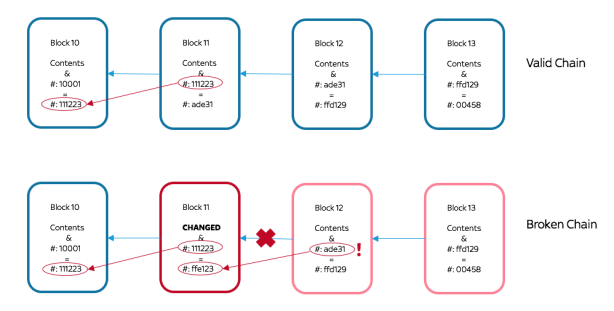
Logo, para os blocos continuarem a formar uma cadeia, é preciso recalcular todos os indicadores (, isto é, o hash do bloco posterior) de todos os blocos que seguem o bloco alterado. Normalmente, estes novos blocos invalidam a blockchain porque estes novos hashes não conformam mais ao padrão requerido (= um número suficiente de dígitos iniciais iguais a ) para ser aceitos na blockchain.
Cada bloco agrupa transações entre os usuários em uma árvore de Merkle.
| Campo | Descrição | Tamanho |
|---|---|---|
| Magic | = 0xD9B4BEF9 | 4 baites |
| Cabeçalho | Contém 6 items | 80 baites |
| Tamanho do Bloco | 4 baites | |
| Número de transações | 1 – 9 baites | |
| Transações |
Cada bloco agrupa transações (que têm, em média, baites). No início, é indicado o seu tamanho (até um Megabaite) e o seu número das transações (em média ).
A primeira transação, a coinbase transação, a recompensa pelo trabalho feito pela sua criação, é alterável pelo criador do bloco e, logo, comumente ele e os seus colaboradores são os destinatários.
As outras transações são transmitidas à rede pelos remetentes, isto é, pagadores, e todos os criadores de blocos, os mineradores, decidem quais transações incluírem no bloco que estão criando. Para incentivar a inclusão de uma transação, o remetente pode pagar uma taxa ao criador do bloco; por isso, frequentemente o minerador inclui tantas transações quanto possíveis, cerca de Megabaite.
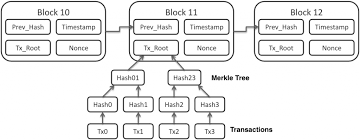
O cabeçalho de cada bloco contém:
nonce, um campo sem conteúdo (semântico); serve para alterar o hash do bloco sem alterar o seu conteúdo (semântico).A função de hash usada pelo Bitcoin é SHA-256. Em mais detalhes:
| Campo | Atualizado quando… | Tamanho |
|---|---|---|
| Versão | o software é atualizado | 4 baites |
| Hash do Bloco anterior | um novo bloco é criado | 32 baites |
| Hash radical da árvore | uma transação foi aceita | 32 baites |
| Data da criação | uns segundos passaram | 4 baites |
| Dificuldade | cada -ésimo bloco | 4 baites |
| Nonce | outro hash é provado | 4 baites |
O “corpo” do bloco, o seu conteúdo (em contraste aos metadados do cabeçalho) são as transações. Estas são agrupadas em uma árvore “de merkle”, uma árvore (normalmente binária) de hashes onde o hash de um nó é calculado pelos dos sucessores; os dados, aqui as transações, constituem as suas folhas.
O nonce serve na busca de um hash para modificar o bloco sem alterar o seu conteúdo. Como mencionamos acima, faz tempo que, quase com certeza, os baites do nonce não são suficientes para encontrar um hash suficientemente pequeno. Isto é, após incrementos, nenhum hash é suficientemente pequeno. Neste caso, o ExtraNonce, a mensagem da coinbase transação (que tem baites) é iterada. Porém, neste caso o hash da raiz da árvore de Merkle precisa de ser recomputada.
A primeira transação, a coinbase transação, a recompensa pelo trabalho feito pela sua criação, é criada pelo criador do bloco e, logo, comumente ele e os seus colaboradores são os destinatários.
Cada transação tem
input, uma entrada, eoutput, uma saída,Todas as transações, exceto a inicial, o input junta outputs de transações (por referir aos seus hashes) cuja soma é maior (ou igual) que a soma dos outputs. Na transação inicial do bloco, o input é arbitrário e a quantia é a recompensa dada ao minerador, inicialmente bitcoins, em 2018.
O primeiro bloco da cadeia, minerado por Satoshi Nakamoto, o pseudónimo do criador anónimo do Bitcoin, contém o título da página um da Financial Times:
The Times 03/Jan/2009
Chancellor on brink of second bailout for banksPorém, como mencionado acima, frequentemente o conteúdo não é legível para o homem; em vez disto, é um valor a fins técnicos, por exemplo, para alterar o bloco tal que o seu hash seja suficientemente pequeno.
Para acrescentar um bloco à blockchain, é preciso dar uma prova de trabalho, o cálculo de (um cabeçalho de) um bloco tal que o seu hash seja pequeno, isto é, que a sua expansão binária começa com um grande número de dígitos zero (atualmente, em agosto de 2018, com zeros na expansão hexadecimal ou zeros na expansão binária). Talvez o software mais usado a este fim seja atualmente CGMiner; existem versões para todos os sistemas operacionais, umas adaptadas para processadores gráfico (GPUs) e outras para processadores especificamente programados para mineração (ASICs).
O hash de um bloco minerado no dia 31 de agosto de 2018:
000000000000000000000e17d5d11694f4602f68a8ab629093a7f61baf6fea77Enquanto o alto custo de trabalho é inútil para erguer uma cadeia de blocos, é essencial para a integridade da cadeia porque impossibilita praticamente a alteração (maléfica) de blocos anteriores; isto é, garante a irreversibilidade da blockchain.
Uma vez a transação é em um bloco da blockchain que foi estendido por, por exemplo, pelo menos cinco, outros blocos, é praticamente impossível substituir os blocos da blockchain por outros (porque enquanto estes blocos são arduamente buscados, a blockchain já foi estendida por outros blocos).
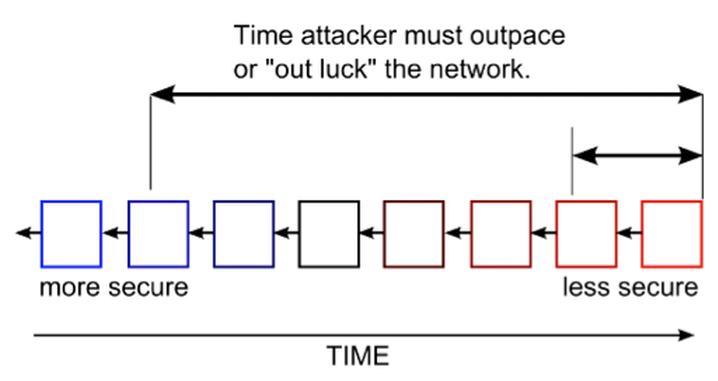
Como cada bloco contém em particular o hash do bloco anterior, e o hash depende dele, a modificação de um bloco necessita a modificação do bloco posterior; como cada bloco precisa de ter um hash que comece com muitos ’s para ser aceito na blockchain, é muito trabalhoso encontrá-los. Um imenso trabalho contra o tempo:
Para alterar um bloco na cadeia, o singelo minerador precisa de

Esta segurança permite dispensar de um terceiro entre os atores, isto é, de uma autoridade fiducial. Em vez dela, os nós da rede acordam sobre a validade da transação.
Porém, se um minerador tem mais força computacional que todos os outros mineradores, então pode aplicar a ataque de :
Uma prova de trabalho é a apresentação de uma informação cuja obtenção é computacionalmente custosa. Frequentemente, o trabalho consiste em realizar um evento pouco provável por muitas repetições, por força bruta.
Bitcoin usa a prova de trabalho introduzida por Hashcash para prevenir spam por uma prova de trabalho para o envio de cada e-mail a cada destinatário; logo, torna o envio em massas custoso.
Em Bitcoin, a prova de trabalho é para a extensão da cadeia por cada novo bloco.
O trabalho consiste em buscar um bloco cujo hash com baites pelo algoritmo SHA-256 seja menor que um certo número alvo:
Outros algoritmos de Hash (em vez de SHA-256) comuns para provas de trabalhos são, por exemplo,
Concatenamos iterativamente à sequência de caracteres “Hello, world!” um número, um nonce, um número a uso único (= once em inglês), tal que (a expansão hexadecimal [com os algarismos e A – F] d’) o seu hash SHA-256 comece com ‘0000’. Existem combinações de quatro dígitos hexadecimais; por isso, se os valores da função hash são uniformemente distribuídos, esperamos cerca de tentativas para encontrá-lo. Com efeito, após tentativas, que levam um milissegundo num computador moderno, obtemos
"Hello, world!0" => 1312AF178C253F84028D480A6ADC1E25...
"Hello, world!1" => E9AFC424B79E4F6AB42D99C81156D3A1...
"Hello, world!2" => AE37343A357A8297591625E7134CBEA2...
...
"Hello, world!4248" => 6E110D98B388E77E9C6F042AC6B49...
"Hello, world!4249" => C004190B822F1669CAC8DC37E761C...
"Hello, world!4250" => 0000C3AF42FC31103F1FDC0151FA7...Porém, em Bitcoin, o objeto hasheado, o cabeçalho do bloco, é mais complexo, em particular, porque contém a raiz da árvore (de Merkle) das transações (= um hash).
O campo dificuldade no cabeçalho do bloco compara
com
No início, para o primeiro bloco, o bloco Génesis, ser aceite na cadeia, a expansão binária do hash do seu cabeçalho precisou de começar com zeros (= o tamanho, em bites, do nonce no cabeçalho do bloco); isto é, eram necessárias (cerca de bilhões) computações de hashes para encontrar um bloco com um tal hash (que levam cerca de minutos em um notebook atual).
Desde então, o número dos zeros é reajustada depois de cada -ésimo bloco para garantir a computação do cabeçalho pela rede levar, em média minutos. (Se a computação de um novo bloco leva, em média, minutos, então a de novos blocos leva, em média, semanas.)
Cada reajuste (após blocos) calcula a nova dificuldade como proporção entre
isto é, Para abrandar saltos, a nova dificuldade é no máximo , isto é, mesmo se (quer dizer, a rede levou menos de três dias e meio), então a nova dificuldade é .
Computar de um cabeçalho de um bloco cujo hash seja menor que o alvo atual, isto é, cuja expansão binária comece com um número suficiente de zeros, é chamada de minerar; o computador que minera (no Brasil) de minerador (para não sobrecarregar o significado da palavra mineiro).
A dificuldade é em cada momento (com uma dilação de cerca de duas semanas) proporcional à juntada força computacional dos mineradores: Quanto mais mineradores, mais difícil, quanto menos mineradores, mais fácil. Atualmente, em 2018, a expansão binária do hash tem de começar com zeros para ser aceito na rede.
Como o hash usado no bitcoin é criptográfico (atualmente SHA-256), isto é, a sua saída não permite deduzir a entrada, a única maneira prática de encontrar um cabeçalho tal que o seu hash seja suficientemente pequeno é a de força bruta, isto é, provar simplesmente todas as possibilidades. Como uma função de hash praticamente é uniformemente aleatória, isto é, as probabilidades entre as saídas são as mesmas, leva para um número (dos dígitos binários iniciais iguais a ) em média cerca de tentativas até encontrar um tal cabeçalho.
Intel Core i7 2600, consegue cerca de milhões hashes por segundo. Por isso, demorará em média cerca de segundos ( anos, isto é, um bilhão de anos) até ele encontrar um bloco que será aceite na cadeia.Isto passa uma ideia da juntada força computacional atual dos mineradores, já que calculam este hash em média em dez minutos.em média Como a função hash usada pelo Bitcoin é SHA-256, como discutido em Seção 10.4, ela é computada rapidamente por um CPU, um microprocessador a uso geral de um computador pessoal, e em particular,
GPU, por um processador gráfico; cerca de vezes mais rápido do que um CPU, eASIC, um microprocessador, ou Circuito Integrado, Adaptado para uma aplicação eSpecífica, aqui a computação do SHA-256; cerca de vezes mais rápido do que um CPU.Com efeito, o gasto de energia para a mineração equivale a cada momento o da Austria inteira. Por isso, surgiram conceitos alternativos à prova de trabalho (= proof of work), por exemplo, a prova de cacife (= proof of stake) onde o criador do bloco é determinado pela sua posse em vez da sua força computacional. Contudo, até agora estes conceitos alternativos não funcionaram tão bem na prática.
Isto dito, uma vez encontrado um tal bloco e o seu hash, dados os dois, a verificação que o hash seja suficientemente pequeno é rápida (e simplesmente consiste em calcular o hash do bloco e comparar com o hash dado).
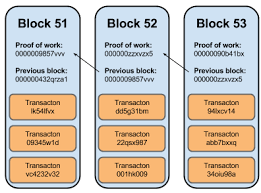
O intervalo para criar um novo bloco é, em média, minutos.
Para alterar o cabeçalho do bloco, recordemo-nos de que os dados variáveis do cabeçalho são (cf. Seção 11.3)
nonce, um campo sem conteúdo (semântico) que serve para alterar o hash do bloco sem alterar o seu conteúdo (semântico).Em particular, o conteúdo principal do bloco, as transações, entram no seu hash só indiretamente pelo hash da raiz da árvore de merkle.
Atualmente, com , como o nonce tem só baites, isto é, bites, raramente (mais exatamente, com uma chance de cerca de ) entre todos os seus possíveis valores encontra-se um tal que o hash do bloco seja suficientemente pequeno. Por isso, modificam-se, além do nonce,
o timestamp, a data de criação em segundos contados desde 1970-01-01 às 00:00 UTC,
as transações, por exemplo, a sua ordem, e
a coinbase, a mensagem (de baites) que acompanha a primeira transação no bloco e transfere uma recompensa ao minerador pelo seu trabalho.
Enquanto a coinbase providencia amplo espaço para alterar o hash, é uma opção mais custosa que o timestamp ou hash, porque, fazendo parte das transações, a sua alteração implica a recomputação dos hashes da árvore de merkle que armazena as transações. (Lembremo-nos de que é só o hash da raiz da árvore que entra no cabeçalho do bloco.)
Ao descobrir um novo bloco, o minerador transmite-o à rede e os nós verificam, entre outros,
Após este bloco ser estendido por pelo menos blocos (e assim a rede ter certeza que ele permaneça na blockchain, a cadeia mais comprida), o descobridor
Como a recompensa diminui gradualmente (até esvair-se após blocos), as taxas terão um papel mais e mais importante para incentivar os mineradores.
Para distribuir mais uniformemente o ganho da mineração, mineradores juntam as suas forças computacionais em grupos, clusters, para compartilharem os bitcoins recompensados.
Todos os bitcoins são gerados por mineração e transferidos aos mineradores, aos criadores do bloco, pela primeira transação de cada bloco, a coinbase que é destinada aos criadores.
Uma vez gerado, um(a moeda de) bitcoin muda de lugar por uma cadeia de assinaturas digitais: O dono transfere o seu bitcoin ao próximo
A soma constada na carteira da interface gráfica Bitcoin Core do bitcoin (desenvolvida inicialmente por Satoshi Nakamoto sob o nome Bitcoin-Qt e usado por dos negociantes) é a soma de todas as transações que o dono da carteira recebeu: Para a Alice pagar certa quantia, por exemplo, bitcoin, ao Bob,
bitcoin,bitcoin ao Bob, ebitcoin à Alice.Isto é, Alice ganhou outra transação (embora de um valor menor que as duas iniciais).
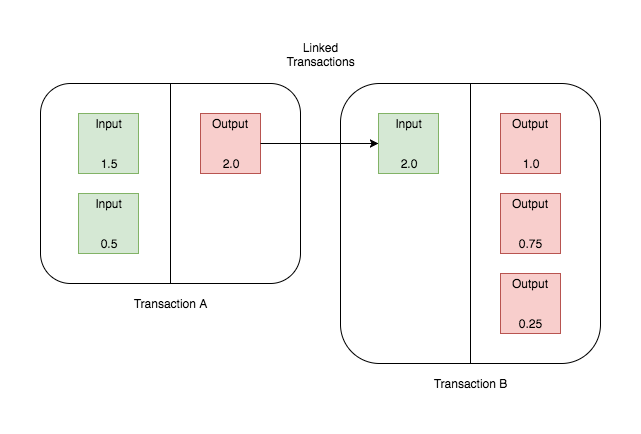
A identidade de cada negociante corresponde à sua chave assimétrica (ECDSA), um par de
Para obter o seu endereço, várias funções de hash são aplicadas à chave pública; a sequência final de letras é codificada pela Base58 cujos algarismos são
0O e as letras Il pelo risco da sua confusão.Para mais detalhes, vide https://gobittest.appspot.com/Address:
Para calcular o hash da chave pública:
ECDSA,RIPEMD-160 (ao último resultado), e0x0000 para P2PKH, 0x0005 for P2SH.Para acrescentar uma soma de verificação:
SHA-256,SHA-256,Para abreviar o resultado (de uma maneira humanamente legível):
Base58.
Para obter o formato do scriptPubkey usado em transações, precisa
Base58 à base hexadecimal,e finalmente acrescenta certo código de instrução.
O uso de um hash em vez da chave pública como endereço,
ECDSA) seja comprometida um dia, eUma transação é uma transferência de bitcoins, primeiro transmitida na rede, em seguida colecionada em um bloco por um minerador e publicado. Todas as transações são públicas, enquanto (os hashes d’) as chaves públicas são anónimas, isto é, não revelam a priori o nome dos donos.
Há dois tipos de transações,
a da geração dos bitcoins ao criar um novo bloco, e
a de negociação entre dois (grupos de) usuários, o remetente e o destinatário.
A transação de negociação tem
um input que refere a saídas de transações em que o remetente recebeu bitcoins, e
um output que transfere aos destinatários uma quantia igual a da soma das saídas das transações da entrada.
Frequentemente, a transação inclui um troco, isto é, o remetente figura como um dos destinatários: Se a soma é menor, a diferença é paga ao criador do bloco como incentivo a incluir a transação.
Uma vez incluída em um bloco na cadeia, e este bloco ser estendido por um número suficiente () de outros, a transação pode ser considerada irreversível, é confirmada.
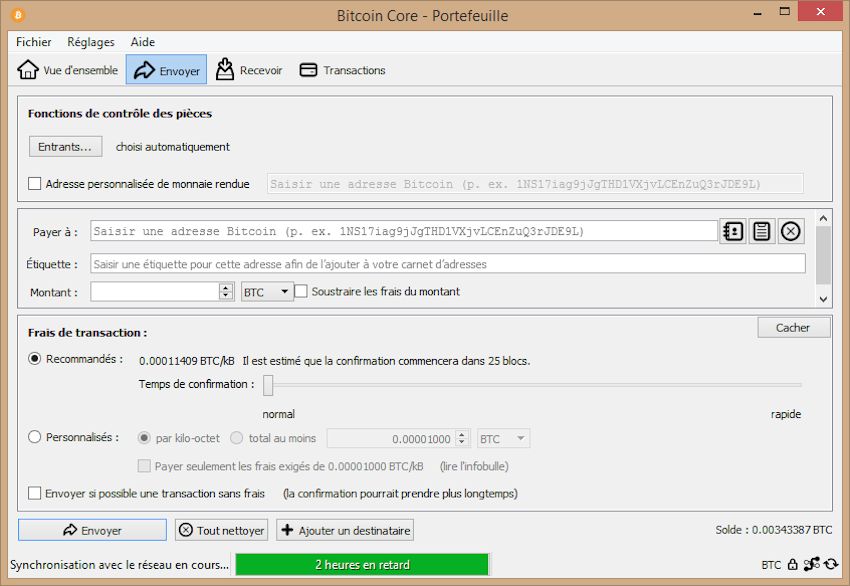
Bitcoin Core. O pagamento de uma taxa de transação ajuda a diminuir o tempo de confirmação.coinbase de baites (em vez de scriptSig) cujo conteúdo é arbitrário. (É frequentemente (ab)usado como ExtraNonce, isto é, Nonce adicional para a mineração, visto que o tamanho do Nonce, baites, atualmente é insuficiente para encontrar um bloco cujo hash sejá suficientemente pequeno. Entretanto, diferente do nonce, o ExtraNonce entra só indiretamente na transação pelo hash da raiz da árvore de Merkle. Logo, a modificação do ExtraNonce requer a recomputação dos hashes do ramo da coinbase na árvore de Merkle das transações.)output distribui a recompensa (de bitcoins em 2018) aos favorecidos pelo minerador.A Alice, para mandar Bitcoins (ou Satoshis) ao Bob,
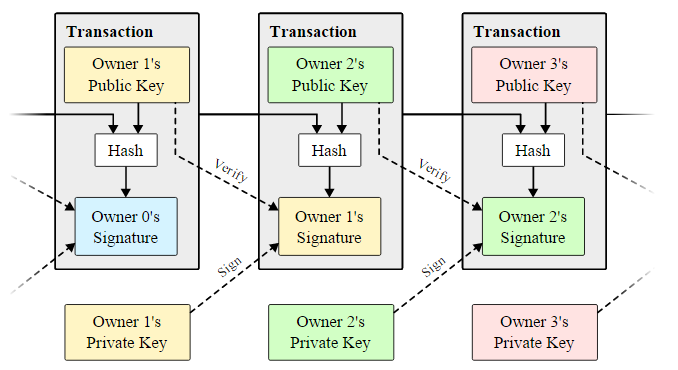
Isto é, Alice demonstra pela sua assinatura que as transações que recebeu pertencem a ela, pois
Os dados principais de uma transação que
coleciona as quantias de uma singela transação na entrada, e
Previous tx: f5d8ee39a4...b9a6
Index: 0
scriptSig: 30450220...1d10
90db022100e2...1501destina um endereço na saída,
Value: 5000000000
scriptPubKey: OP_DUP OP_HASH160.4043...9d
OP_EQUALVERIFY OP_CHECKSIGA entrada, o input, nesta transação recebe BTC da saída, do output, em transação e envia os, isto é, BTC ao endereço Assina todas estas informações por 30450 ....
O input é uma referência a uma saída de uma transação anterior, frequentemente, uma transação tem várias. A sua soma (menos uma opcional taxa de transação paga ao minerador para inclui-la no seu bloco) é esgotada nas saídas da transação. No exemplo
Previous tx é o hash da transação anterior,
Index é a saída da transação referida, e
ScriptSig é a primeira metade, uma assinatura, de um script que concatena, principalmente,
A chave pública tem de coincidir com a dada pelo hash no índice do output da transação anterior, e é usada para verificar a assinatura (em mais detalhes, uma assinatura pelo algoritmo ECDSA com a curva secp256k1 de um hash da transação). A chave pública e a assinatura garantem a transação ser criada pelo destinatário da saída da transação anterior. Os dados assinados consistem principalmente
a quantia, e
o output script que usualmente consiste na instrução
OP_DUP OP_HASH160 06f1b... OP_EQUALVERIFY OP_CHECKSIGcujo código hexadecimal 06f1b... indica o endereço do destinatário.
O output instruí o envio da soma dos bitcoins da entrada:
Value é o número de Satoshi (onde BTC = Satoshi) do valor do output, e
O output script, usualmente scriptPubKey que indica o endereço (= um hash de uma chave pública). Mais exatamente, um script é uma sequência de instruções que começa com OP_ (OP_DUP, …) formulada na linguagem Script; por exemplo,
OP_DUP (0x76)
OP_HASH160 (0xa9)
0x14 (= indica que 20 baites de dados seguem)
cba5...e8 (os dados)
OP_EQUALVERIFY (0x88)
OP_CHECKSIG (0xac)o que é concatenada a
OP_DUP OP_HASH160 cba5f7...9ee8 OP_EQUALVERIFY OP_CHECKSIGPara o transporte e a assinatura, todas as instruções são codificadas por baites
76a914cba5f746dc1e41a932a7d38be7aba95944619ee888acTodo output pode ser referido uma única vez só em uma transação posterior; por isso, para evitar perda, a soma inteira do input precisa ser enviada! Por exemplo, se a soma da entrada é BTC, mas o usuário quer apenas pagar BTC, então ele cria dois ouputs,
BTC para o destinatário, eBTC para ele, o remetente (= o troco).Toda a quantia que não foi gastada será considerada uma taxa de transação, isto é, transferida ao criador do bloco (como incentivo de incluir esta transação antes de outras).
Na rede do bitcoin, há
Um minerador é incentivado
Porém, em geral, não é incentivado a enviar o bloco minerado por outrem; em vez disto, esconde a sua existência até ter minerado um próprio bloco que o estende. Esta transmissão instantânea cabe aos nós.
Um usuário é incentivado a manter um nó para poder a todo ponto garantir a integridade da blockchain. Porém, a manutenção de um nó inteiro é sobretudo uma necessidade altruísta que é essencial para o funcionamento do Bitcoin: É só razoavelmente seguro usar um nó parcial (que não tem a cadeia inteira) enquanto a maior parte da rede são nós inteiros que garantem a validade.
Resumimos o processamento de uma transação, desde a sua emissão até a sua conclusão:
O usuário envia uma transação pelo seu aplicativo de carteira.
A transação é difusa pelos nós e faz parte do ‘acervo de transações não-confirmadas’.
Mineradores,
comumente, até esgotar o tamanho máximo do bloco (de Megabaite).
Cada minerador tenta de modificar o bloco de tal maneira que o seu hash seja suficientemente pequeno (por exemplo, atualmente, que comece com baites nulos). A probabilidade de encontrar um tal bloco, isto é, a dificuldade do problema, é a mesma para todos os blocos e mineradores. Esta dificuldade é ajustada cada -ésimo bloco (isto é, após cerca duas semanas) dependendo da força computacional total dos mineradores para um tal bloco sempre ser encontrado em média em dez minutos.
Quando um novo bloco é concatenado à cadeia, todos os mineradores têm de recomeçar com outro bloco, já que, por exemplo,
Todo minerador que encontra um bloco válido transmite-o aos nós da rede.
O nó verifica se o bloco seja válido, isto é,
Se o nó acorda sobre a validade do bloco, então o concatenam à cadeia. Uma confirmação de uma transação é cada extensão da cadeia por um bloco após aquele que contém a transação. A extensão da cadeia pelo bloco que contém a transação conta como primeira confirmação, a após este bloco como segunda confirmação, e assim por diante. A chance da cadeia mudar após seis confirmações (isto é, após, em média, uma hora) é minúscula; por isso, comumente, uma transação é vista como conclua após a sexta confirmação.
Para o nó verificar rapidamente a validade da entrada de uma transação, isto é, se as transações redimidas não foram gastadas ainda, ele atualiza a cada momento o banco-de-dados Unspent Transaction Ouput (UTXO) de todas as transações que ainda não foram gastadas. Atualmente, o UTXO tem cerca de GB e é guardada na memória para garantir consultas rápidas.
Recordemo-nos de que cada transação é única, e pode ser gastada apenas uma vez, e inteiramente (para obter o troco, cria se outra transação). Quando uma transação é transmitida,
UTXO, eUTXO.Para impedir o gasto duplo, o nó verifica se uma transação é no UTXO: caso sim, permite a transação, caso contrário, a impede.
Uma confirmação de uma transação é cada extensão da cadeia por um bloco após aquele que contém a transação. A extensão da cadeia pelo bloco que contém a transação conta como primeira confirmação, a após este bloco como segunda confirmação, e assim por diante.
A chance da cadeia mudar após seis confirmações (isto é, após, em média, uma hora) é minúscula; por isso, comumente, uma transação é considerada conclusa após a sexta confirmação. Por exemplo, a interface gráfica padrão para o bitcoin, o Bitcoin Core, mostra uma transação como confirmada quando a profundeza da transação atingiu blocos.
Porém, esta profundeza, o número de confirmações para bitcoins transferidos, de blocos é arbitrária, e pode mudar com cada transação. Em contraste, bitcoins minerados só podem ser gastados quando o bloco gerado tem uma profundeza de blocos, isto é, foi estendido na cadeia por blocos.
Bach, Eric. 1984. Discrete Logarithms and Factoring. Computer Science Division, University of California Berkeley.
Daemen, Joan. 1995. «Cipher and hash function design strategies based on linear and differential cryptanalysis». Tese de doutoramento, Doctoral Dissertation, March 1995, KU Leuven.
Daemen, Joan, e Vincent Rijmen. 1999. «AES proposal: Rijndael». http://www.cs.miami.edu/home/burt/learning/Csc688.012/rijndael/rijndael_doc_V2.pdf.
———. 2002. The design of Rijndael. Information Security and Cryptography. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-662-04722-4.
Diffie, Whitfield, e Martin Hellman. 1976. «New directions in cryptography». IEEE transactions on Information Theory 22 (6): 644–54.
Goldwasser, Shafi, e Silvio Micali. 1984. «Probabilistic encryption». J. Comput. System Sci. 28 (2): 270–99. https://doi.org/10.1016/0022-0000(84)90070-9.
Gordon, Daniel M. 1993. «Discrete logarithms in using the number field sieve». SIAM J. Discrete Math. 6 (1): 124–38. https://doi.org/10.1137/0406010.
Heys, Howard M. 2002. «A tutorial on Linear and Differential Cryptanalysis». Cryptologia 26 (3): 189–221.
Hoffstein, Jeffrey, Jill Catherine Pipher, e Joseph H Silverman. 2008. An Introduction to Mathematical Cryptography. Vol. 1. Springer.
Joux, Antoine. 2009. Algorithmic cryptanalysis. Chapman & Hall/CRC Cryptography and Network Security. CRC Press, Boca Raton, FL. https://doi.org/10.1201/9781420070033.
Joux, Antoine, e Kim Nguyen. 2003. «Separating decision Diffie-Hellmann from computational Diffie-Hellman in cryptographic groups». J. Cryptology 16 (4): 239–47. https://doi.org/10.1007/s00145-003-0052-4.
Lenstra, A. K., H. W. Lenstra Jr., M. S. Manasse, e J. M. Pollard. 1993. «The number field sieve». Em The development of the number field sieve, 1554:11–42. Lecture Notes in Math. Springer, Berlin. https://doi.org/10.1007/BFb0091537.
Maurer, Ueli M., e Stefan Wolf. 1999. «The relationship between breaking the Diffie-Hellman protocol and computing discrete logarithms». SIAM J. Comput. 28 (5): 1689–1721. https://doi.org/10.1137/S0097539796302749.
Menezes, Alfred J., Paul C. van Oorschot, e Scott A. Vanstone. 1997. Handbook of applied cryptography. CRC Press Series on Discrete Mathematics and its Applications. CRC Press, Boca Raton, FL. http://www.cacr.math.uwaterloo.ca/hac/.
Rivest, Ronald L, Adi Shamir, e Leonard Adleman. 1978. «A method for obtaining digital signatures and public-key cryptosystems». Communications of the ACM 21 (2): 120–26.
Shoup, Victor. 1997. «Lower bounds for discrete logarithms and related problems». Em Advances in cryptology—EUROCRYPT ’97 (Konstanz), 1233:256–66. Lecture Notes in Comput. Sci. Springer, Berlin. https://doi.org/10.1007/3-540-69053-0_18.
Sweigart, Albert. 2013. Hacking Secret Ciphers with Python. Gratis.